一、关键路径及参数

1.1 AOE网介绍

在介绍本节主题之前，先来介绍一下AOE网
AOE网是一个带权的有向无环图，用：

顶点表示事件
弧表示活动,
权值表示活动持续时间

如下图，
在这里插入图片描述
用 V1到V9表示工程的开始和结束，a1到a11表示11项活动。权值表示活动持续天数。例如：活动 a2 持续时间为 4 天

前面说过，AOE网是一个带权的有向无环图。

带权的含义上文已经说明。
有向表示活动之间的顺序。
无环:a活动结束，b才能开始。如果同时b结束a才能开始，那么工程肯定无法开始。因为ab互相依赖。这就是无环的含义

1.2 时间参数介绍

关键路径：关键路径即完成工程中，路径长度最长的路径。

比如上图中，v1,v2,v5,v7,v9，这条路径的权值之和最大，为18，一旦该路径上的某项活动拖慢进度，必然导致整个工程时间变长。
关键路径可以不只一条。比如上图中，v1,v2,v5,v8,v9 为18，也是关键路径

最早发生时间：vi 的最早开始时间为，从开始点到 vi 的最长路径。例如图中 v5
在这里插入图片描述
v5的开始，依赖于 v2和v3的结束。所以v5的最早开始时间，为 v2和v3结束时间的最大值。

最迟开始时间：在不推迟整个工程完成的情况下，活动最迟必须开始的时间。

既然 v5 最早在第7天才能开始，那么 v3 显然不那么着急。只要保证第7 天之前完成 a5 即可。所以我们可以定义一个最迟开始时间

总时差:
用 e(i)表示活动 i 最早开始时间（early)，l(i)表示活动 i 最迟开始时间
TF表示总时差，则
$T F = l (i) ? e (i)$
表示完成活动的剩余时间量。在总时差内，可以拖。
v5 的最早开始时间为 7，所以 a5 的最迟发生时间为 7-a5 = 6。
而 v3 的最早开始时间为 4，所以 a5 可以在 a2 完成后，再推迟 2 天开工，也不会影响到总工期

关键活动：影响到总工期的活动即为关键活动。通过上面的例子我们可以知道，关键活动就是最迟发生时间等于最早发生时间的活动。
$e (i) = l (i)$
因为一天都不能拖。关键路径，即为关键活动连成的路径

为了求得活动的 e(i)和 l(i)，首先要求出事件的最早发生时间ve(j)和事件最迟发生时间vl(j)
假设活动 ai由弧 <j,k>表示，持续时间记为
$d u t (< j, k >)$
则有如下关系
$e (i) = v e (j)$
$l (i) = v l (k) ? d u t (< j, k >)$

求ve(j)，从前往后
$v e (0) = 0$
$ve(j)=Max\{ve(i)+dut(<i,j>)\}$
j 只有在前面所有紧前工作完成后，才能开始。
v(j)的最早发生时间，为紧前工作的最早发生时间，加上紧前工作持续时间，取最大值。因为事件可能有多个紧前工作。
开始活动的最早发生时间为 0

求vl(i)，逆推法从后往前
$vl(i)=Min\{vl(j)-dut(<i,j>)\}$
i 最慢，在紧后工作最迟开始之前要完成
事件最迟发生时间，为紧后工作的最迟发生时间，减去活动的持续时间。

二、找出关键路径

2.1 ve(i)

开始活动为0

v	1	2	3	4	5	6	7	8	9
ve(i)	0

v2，v3，v4 只有 v1 一个紧前工作，所以 ve 值为 ve(1) 加上 a1，a2，a3 的权

v	1	2	3	4	5	6	7	8	9
ve(i)	0	6	4	5

v5 有 v2，v3 两个紧前工作，ve(5) 为 v2+a4 ，v3+a5 取最大值
注意： a4 的开始、结束事件为 v2，v5，a5的事件为 v3，v5

v	1	2	3	4	5	6	7	8	9
ve(i)	0	6	4	5	7

同理，可求出剩余

v	1	2	3	4	5	6	7	8	9
ve(i)	0	6	4	5	7	7	16	14	18

2.2 vl(i)

从后往前推，多个情况选最小值

v	1	2	3	4	5	6	7	8	9
vl(i)	0	6	6	8	7	10	16	14	18

对比 vl 与 ve，当
$v e (i) = v l (i)$
时，即为关键路径

三、代码实现

3.1 C语言版

# include <stdio.h>
# include <string.h>
# include <stdlib.h>

# define true 1
# define false 0
# define max 999
# define MAX_SIZE 20

typedef int bool;

typedef struct {
    int data[MAX_SIZE];
    int end;
} stack, *pstack;

// 栈
pstack CreateStack();
void push(pstack ps, int val);
bool empty(pstack ps);
int pop(pstack ps);
// 图
int **Matrix(int size);
// 关键路径
void KeyPath(int **matrix, int size);

int main() {
    int size;
    printf("size:");
    scanf("%d", &size);
    int **matrix = Matrix(size);
    KeyPath(matrix, size);

    return 0;
}

pstack CreateStack() {
    pstack ps = (pstack) malloc(sizeof(stack));
    memset(ps, 0, sizeof(stack));
    return ps;
}

bool empty(pstack ps) {
    if (ps->end==0) {
        return true;
    } else {
        return false;
    }
}

void push(pstack ps, int val) {
    // ps->end < MAX_SIZE
    ps->data[ps->end++] = val;
}

int pop(pstack ps) {
    if (!empty(ps)) {
        return ps->data[--ps->end];
    } else {
        return -1;
    }
}

int **Matrix(int size) {
    int **matrix = (int **) malloc(sizeof(int *)*size);
    for (int i=0; i<size; i++) {
        matrix[i] = (int *) malloc(sizeof(int)*size);
    }

    for (int i=0; i<size; i++) {
        for (int j=0; j<size; j++) {
            scanf("%d", &matrix[i][j]);
        }
    }
    return matrix;
}

void KeyPath(int **matrix, int size) {
    int ve[size], vl[size];
    memset(ve, 0, sizeof(ve));
    memset(vl, 0x3f, sizeof(ve));

    pstack ps = CreateStack();

    // 找到开始节点
    bool flag = false;
    for (int i=0; i<size; i++) {
        for (int j=0; j<size; j++) {
            if (matrix[j][i]!=0) {
                flag = true;
                break;
            }
        }
        if (flag==false) {
            push(ps, i);
            ve[i] = 0;
            break;
        }
    }

    // 求 ve(i)
    while (!empty(ps)) {
        int index = pop(ps);
        // 找到与 index 顶点相连边
        for (int i=0; i<size; i++) {
            if (matrix[index][i]!=0) {
                push(ps, i);
                // ve(j) = max{ve(i)+dut(<i,j>)}
                if (ve[index]+matrix[index][i]>ve[i]) {
                    ve[i] = ve[index]+matrix[index][i];
                }
            }
        }
    }

    vl[size-1] = ve[size-1];

    for (int i=size-1; i>=0; i--) {
        // 找到和 i 连通的点 
        // vl(i)=Min{vl(j)?dut(<i,j>)}
        for (int j=0; j<size; j++) {
            if (matrix[i][j]!=0 && vl[i]>vl[j]-matrix[i][j])
                vl[i] = vl[j] - matrix[i][j];
        }
    }
    printf("ve:\t");
    for (int i=0; i<size; i++) {
        printf("%d\t", ve[i]);
    }
    printf("\n");
    printf("vl:\t");
    for (int i=0; i<size; i++) {
        printf("%d\t", vl[i]);
    }
    printf("\n");
    printf("关键活动:\t");
    for (int i=0; i<size; i++) {
        if (ve[i]==vl[i]) {
            printf("V%d\t", i+1);
        }
    }
    printf("\n");
}

3.2 java

package src;

import java.util.Arrays;
import java.util.Scanner;
import java.util.Queue;
import java.util.LinkedList;

public class KeyPath {
    public static void main(String[] args) {
        int[][] matrix = createMatrix();
        keyPath(matrix);
    }

    public static void keyPath(int[][] matrix) {
        Queue<Integer> q = new LinkedList<Integer>();

        int[] ve = new int[matrix.length],
                vl = new int[matrix.length];

        // ve
        q.add(0);
        while (q.isEmpty()==false) {
            int get = q.poll();
            // 找到和 get 连通的顶点
            for (int i=0; i<matrix.length; i++) {
                if (matrix[get][i]!=0) {
                    q.add(i);
                    ve[i] = Math.max(ve[i], ve[get]+matrix[get][i]); // max {ve(i)+dut(<i,j>)
                }
            }
        }

        // vl
        Arrays.fill(vl, ve[matrix.length-1]);
        for (int i=matrix.length-1; i>=0; i--) {
            // 找到和 i 连通的边
            for (int j=0; j<matrix.length; j++) {
                if (matrix[i][j]!=0) {
                    vl[i] = Math.min(vl[i], vl[j]-matrix[i][j]);
                }
            }
        }

        // 输出
        System.out.println("ve:\t" + Arrays.toString(ve));
        System.out.println("vl:\t" + Arrays.toString(vl));
        System.out.print("关键路径:\t");
        for (int i=0; i<matrix.length; i++) {
            if (ve[i]==vl[i]) {
                System.out.format("V%d\t", i+1);
            }
        }
        System.out.println();
    }

    public static int[][] createMatrix() {
        Scanner sc = new Scanner(System.in);

        System.out.print("size = ");
        int size = sc.nextInt();
        int[][] matrix = new int[size][size];

        System.out.println("matrix : ");
        for (int i=0; i<size; i++) {
            for (int j=0; j<size; j++) {
                matrix[i][j] = sc.nextInt();
            }
        }
        return matrix;
    }
}

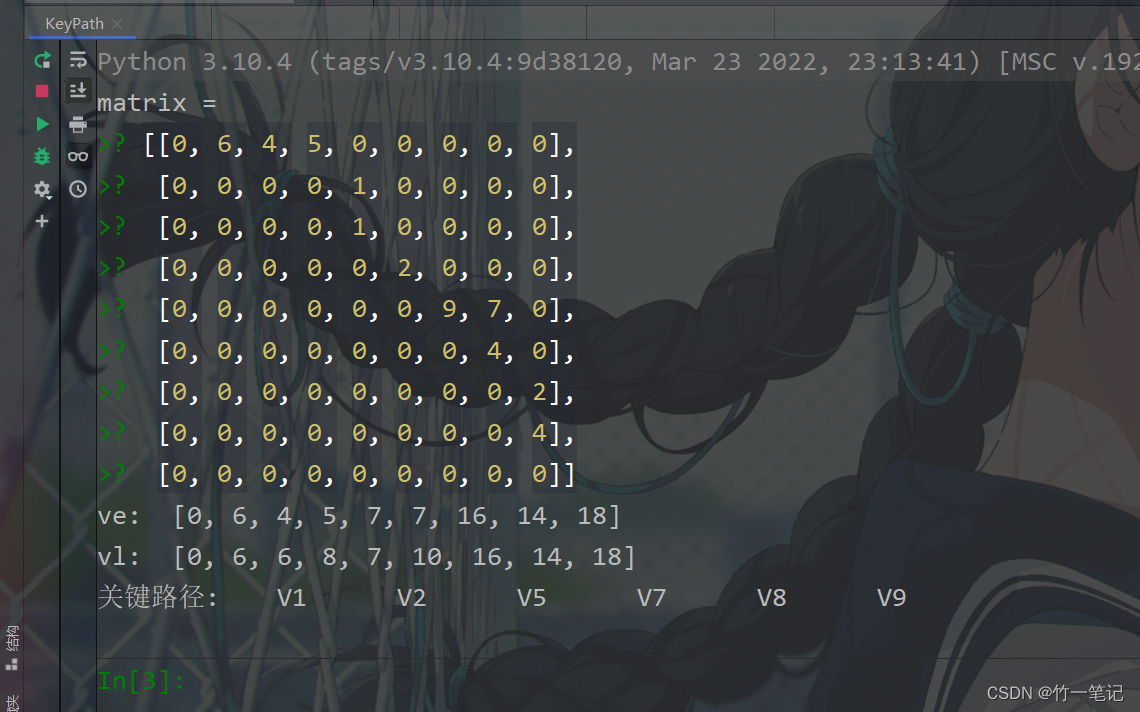
3.3 Python

import queue
import json

class KeyPath:
    def createMatrix(self)->list:
        return json.loads(input("matrix = \n"))

    def keyPath(self, matrix):
        ve = [0 for i in range(len(matrix))]

        q = queue.Queue()
        q.put(0)
        # 求 ve
        while not q.empty():
            index = q.get()
            for i in range(len(matrix)):
                if matrix[index][i]:
                    ve[i] = max(ve[i], ve[index]+matrix[index][i])
                    q.put(i)

        # 求 vl
        vl = [ve[-1] for i in range(len(matrix))]
        for i in range(len(matrix)-1, -1, -1):
            for j in range(len(matrix)):
                if matrix[i][j]:
                    vl[i] = min(vl[i], vl[j]-matrix[i][j])

		# 输出
        print("ve:\t", ve)
        print("vl:\t", vl)
        print("关键路径:", end="\t")
        for i in range(len(ve)):
            if ve[i]==vl[i]:
                print("V{}".format(i+1), end="\t\t")
        print()

    def run(self):
        matrix = self.createMatrix()
        self.keyPath(matrix)


if __name__ == '__main__':
    kp = KeyPath()
    kp.run()

3.4 运行示例

在这里插入图片描述
该图用邻接矩阵可表示为

0 6 4 5 0 0 0 0 0
0 0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0 0
0 0 0 0 0 2 0 0 0
0 0 0 0 0 0 9 7 0
0 0 0 0 0 0 0 4 0
0 0 0 0 0 0 0 0 2
0 0 0 0 0 0 0 0 4
0 0 0 0 0 0 0 0 0

数组表示
python列表：
[[0, 6, 4, 5, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 1, 0, 0, 0, 0],
 [0, 0, 0, 0, 1, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 2, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 9, 7, 0],
 [0, 0, 0, 0, 0, 0, 0, 4, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 2],
 [0, 0, 0, 0, 0, 0, 0, 0, 4],
 [0, 0, 0, 0, 0, 0, 0, 0, 0]]

size = 9

c语言：
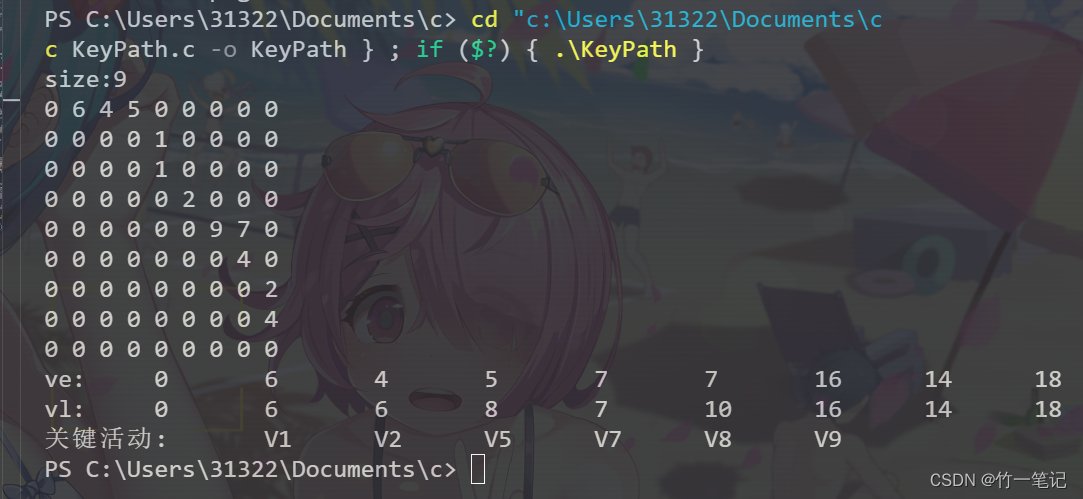
在这里插入图片描述
java:

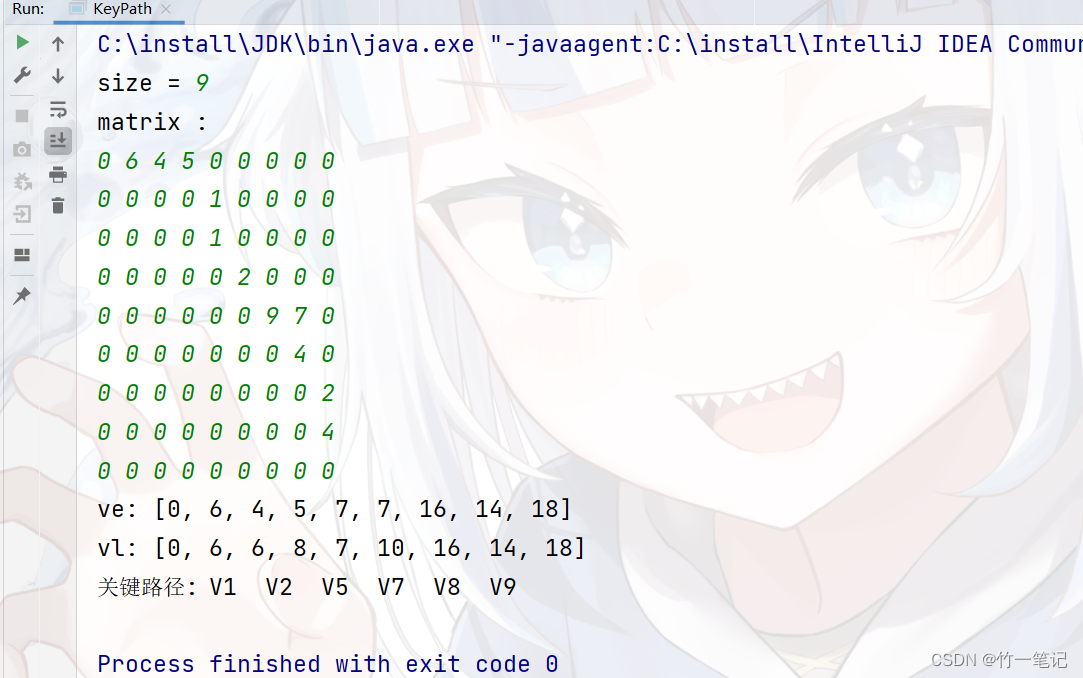
python