题目要求

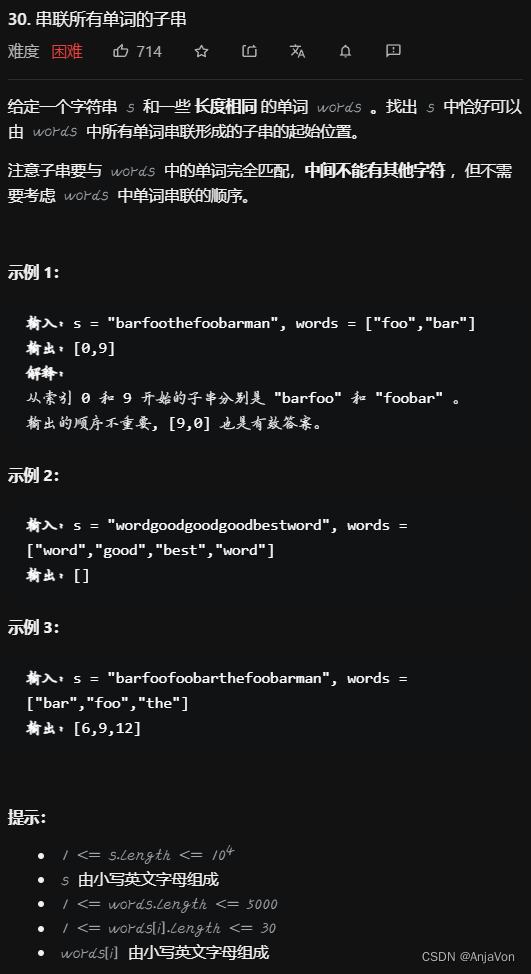
在这里插入图片描述

思路：滑动窗口

用目标子串的大小作为窗口大小，遍历整个字符串找结果；
为了便于剪枝，减少比较与开销，枚举起始点时
- 可以将起点根据当前下标与单词长度的取余结果进行分类，这样就不用频繁的建立新的哈希表和进行单词统计。
- 每次记录当前窗口内出现的单词，用于和给出的 $w o r d s$ 比较判断；
- 当长度超了窗口范围，把前面的单词丢出去维持窗口大小；
- 同时注意比较每个加入的单词是否存在于 $w o r d s$ 中，不存在直接剪枝到下一轮判断。

Java

class Solution {
    public List<Integer> findSubstring(String s, String[] words) {
        int sl = s.length(), wl = words.length, ww = words[0].length();
        Map<String, Integer> freq = new HashMap<>();
        for (String w : words) // 统计每个单词及其出现的次数
            freq.put(w, freq.getOrDefault(w, 0) + 1);
        List<Integer> res = new ArrayList<>();
        for (int i = 0; i < ww; i++) {
            Map<String, Integer> win = new HashMap<>(); // 记录当前子串中出现的单词
            for (int j = i; j + ww <= sl; j += ww) {
                String cur = s.substring(j, j + ww); // 当前单词
                win.put(cur, win.getOrDefault(cur, 0) + 1);
                if (j >= i + (wl * ww)) { // 长度超了
                    int idx = j - wl * ww;
                    String pre = s.substring(idx, idx + ww);
                    // 删掉第一个单词
                    if (win.get(pre) == 1)
                        win.remove(pre);
                    else
                        win.put(pre, win.get(pre) - 1);
                    if (!win.getOrDefault(pre, 0).equals(freq.getOrDefault(pre, 0))) // 单词不同，剪枝
                        continue;
                }
                if (!win.getOrDefault(cur, 0).equals(freq.getOrDefault(cur, 0))) // 单词不同，剪枝
                    continue;
                if (win.equals(freq)) // win与freq中单词完全相同
                    res.add(j - (wl - 1) * ww);
            }
        }
        return res;
    }
}

时间复杂度： $O(wl+ww\times sl)$ ，统计单词及出现次数复杂度为 $O (w l)$ ；枚举取余的结果（ $i$ 循环）复杂度为 $O (w w)$ ；每次循环最多处理长度为 $s l$ 的字符串。
- 由于字符串长度固定且不超过 $30$ ，假定所有哈希操作均为 $O (1)$ 的；
空间复杂度： $O(wl\times ww)$

Rust

use std::collections::HashMap;
impl Solution {
    pub fn find_substring(s: String, words: Vec<String>) -> Vec<i32> {
        let mut res = Vec::new();
        let (wl, ww, sl) = (words.len(), words[0].len(), s.len());
        if sl == 0 || wl == 0 || sl < wl * ww {
            return res;
        }
        let sb = s.as_bytes();
        let mut freq = HashMap::with_capacity(ww * 2);
        words.into_iter().for_each(|w| *freq.entry(w).or_insert(0) += 1);
        (0..=sl - wl * ww).filter(|i| {
            let mut win = HashMap::new();
            (0..wl).for_each(|j| {
                *win.entry(String::from_utf8(sb[(i + j * ww)..(i + (j + 1) * ww)].to_vec()).unwrap()).or_insert(0) += 1;
            });
            freq == win
        }).map(|i| i as i32).collect::<Vec<i32>>()        
    }
}

时间复杂度： $O(wl+ww\times sl)$ ，统计单词及出现次数复杂度为 $O (w l)$ ；枚举取余的结果（ $i$ 循环）复杂度为 $O (w w)$ ；每次循环最多处理长度为 $s l$ 的字符串。
- 由于字符串长度固定且不超过 $30$ ，假定所有哈希操作均为 $O (1)$ 的；
空间复杂度： $O(wl\times ww)$

C++

【在用例86上卡了，返回了空……没太搞懂为啥，就换了官方的思路】

记录窗口中出现的单词，并根据 $w o r d s$ 所需维护还需要的单词个数。
也就是说前面的 $w i n$ 存的是窗口内已有的单词数（所以最后应该和 $w o r d s$ 相等），而C++里的存的是还需要的单词数（所以最后应该空）。

class Solution {
public:
    vector<int> findSubstring(string s, vector<string>& words) {
        vector<int> res;
        int sl = s.size(), wl = words.size(), ww = words[0].size();
        for (int i = 0; i < ww && i + wl * ww <= sl; i++) {
            unordered_map<string, int> win;
            for (int j = 0; j < wl; j++)
                win[s.substr(i + j * ww, ww)]++; // 在窗口内
            for (string &w : words) {
                if (--win[w] == 0) // 在word内
                    win.erase(w);
            }
            for (int k = i; k < sl - wl * ww + 1; k += ww) {
                if (k != i) {
                    string cur = s.substr(k + (wl - 1) * ww, ww);
                    if (++win[cur] == 0)
                        win.erase(cur);
                    cur = s.substr(k - ww, ww);
                    if (--win[cur] == 0)
                        win.erase(cur);
                }
                if(win.empty()) // word中所有单词都在窗口中出现
                    res.emplace_back(k);
            }
        }
        return res;
    }
};