这场质量极高,可惜的是在外面(WB)打的,导致打的状态不好,也没有草稿本,只能颅内摸你😟。
PS:前两场打的心态有点炸(一场UR,一场阅读理解)没更新,之后会补上。
赛中过了A~D,E想了半个多小时没构造出来(颅内摸你太难了),然后A了F1,F2来不及写了(doge)。
A. Download More RAM(贪心/sort/摸你)
题意是有n中内存条每种最多用一次,初始有n空间,第i个内存条需要占用ai空间,可以带来bi收益,且用过的空间会回归,因此只需以ai升序贪心即可。
#include <bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
#define Ma 1000005
#define mod 1000000007
using namespace std;
struct node
{
ll a,b;
bool operator <(const node &A)const{
return a<A.a;
}
}t[Ma];
int main()
{
ll tt;
scanf("%lld",&tt);
while (tt--)
{
ll n,k;
scanf("%lld%lld",&n,&k);
for (ll i=1;i<=n;i++)
scanf("%lld",&t[i].a);
for (ll i=1;i<=n;i++)
scanf("%lld",&t[i].b);
sort(t+1,t+n+1);
ll ma=k;
for (ll i=1;i<=n;i++)
if (ma>=t[i].a)
ma+=t[i].b;
printf("%lld\n",ma);
}
return 0;
}B. GCD Arrays(思维+数学)
假设我们最终的gcd为x,我们可以发现(x>2&&len>=2,len表示[l,r]的长度),因此可以得到gcd为2时为最优解,因此只要删除[l,r]中奇数情况即可,当然需要特判下len=1时的情况。
#include <bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
#define Ma 1000005
#define mod 1000000007
using namespace std;
ll a[Ma];
int main()
{
ll tt;
scanf("%lld",&tt);
while (tt--)
{
ll a,b,k;
scanf("%lld%lld%lld",&a,&b,&k);
ll mi=b/2-(a-1)/2;
if (mi==0&&a!=1&&b!=1)
mi=1;
if (b-a+1-mi>k)
printf("NO\n");
else
printf("YES\n");
}
return 0;
}C. Meximum Array(思维+贪心)
首先题目意思是让你得出一个字典序最大的b,假设这个字典序最大的b中存在bi<bi+1,那么一定可以将bi+1合并到bi中一使b更大,因此b是非升序列。
其次我们要了解下MEX,我们可以假设bi=x,若没有x-1这个数字,那么就将bi更新至x-1,否则维护x-1的最优加入。
#include <bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
#define Ma 1000005
#define mod 1000000007
using namespace std;
ll ans[Ma];
ll add=0;
vector <ll> a[Ma];
ll tot[Ma];
int main()
{
ll tt;
scanf("%lld",&tt);
while (tt--)
{
add=0;
ll n;
scanf("%lld",&n);
for (ll i=0;i<=n;i++)
a[i].clear(),tot[i]=0;
for (ll i=1;i<=n;i++)
{
ll x;
scanf("%lld",&x);
a[x].push_back(i);
}
ans[0]=n;
ll p=0;
while (p<n)
{
ll ne=p+1;
for (ll i=ans[add];i>=0;i--)
{
while (tot[i]<a[i].size()&&a[i][tot[i]]<=p)
tot[i]++;
if (tot[i]<a[i].size())
ne=max(ne,a[i][tot[i]]);
else
ans[add]=i,ne=p+1;
}
ans[add+1]=ans[add];
add++;
p=ne;
}
printf("%lld\n",add);
for (ll i=0;i<add;i++)
printf("%lld ",ans[i]);
}
return 0;
}D. Peculiar Movie Preferences(思维+字符串+匹配)
首先我们发现若有len=1的字符串则直接输出YES,否则我们可以假设有回文串s,由于2<=len<=3,他拼接的头串和尾串也一定能组成回文串,因此拼接字符串一定<=2,即可通过匹配得出
PS:题目的字符串拼接具有先后顺序,博主因为写的太臭+没注意细节wa了2发(GG)
#include <bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
#define Ma 1000005
#define mod 1000000007
using namespace std;
ll l[26][26];
ll add[26][26][26];
int main()
{
ll tt;
scanf("%lld",&tt);
while (tt--)
{
memset(l,0,sizeof(l));
memset(add,0,sizeof(add));
ll n;
ll flag=0;
scanf("%lld",&n);
for (ll i=1;i<=n;i++)
{
string s;
cin>>s;
if (s.size()==1)
flag=1;
else if (s[0]==s[s.size()-1])
flag=1;
else if (s.size()==2)
{
ll x=s[0]-'a',y=s[1]-'a';
if (l[y][x])
flag=1;
for (ll i=0;i<26;i++)
if (add[y][x][i])
flag=1;
l[s[0]-'a'][s[1]-'a']=1;
}
else
{
ll x=s[0]-'a',y=s[1]-'a',z=s[2]-'a';
if (l[z][y])
flag=1;
if (add[z][y][x])
flag=1;
add[s[0]-'a'][s[1]-'a'][s[2]-'a']=1;
}
}
if (flag)
printf("YES\n");
else
printf("NO\n");
}
return 0;
}E. Grid Xor(思维+构造+xor)
首先这题我开始没想出来,后面想到可一个构造方法(与题目题解不同,题目题解U1S1挺离谱的,T1看的不是很懂,T2好像不能实现(好像只有在4n+2的情况下可以))。
首先我们可以发现的是红白格相互独立,并不影响,因此我们以红格为例:
?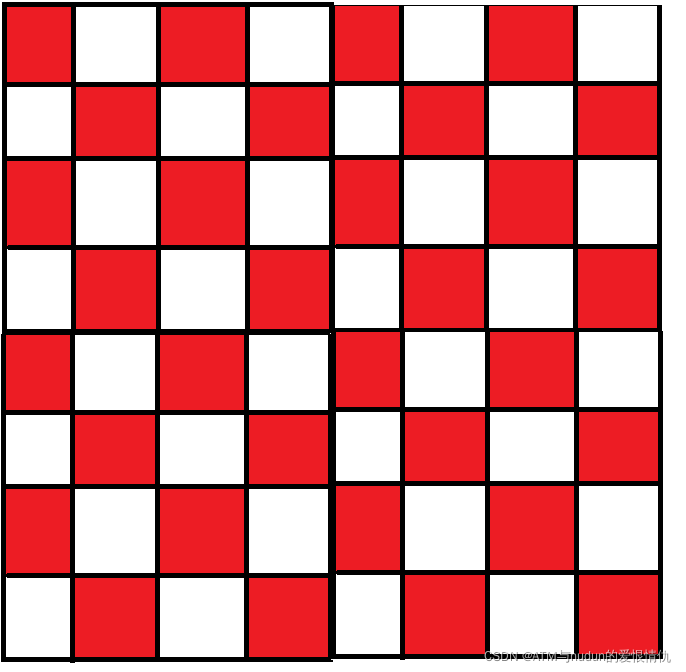
我们可以看到以下情形:
A操作可以得出1
B操作可以得出1 XOR 2
C操作可以得出2?XOR 3
.。。。。。。
因此递推即可得出所有段的值
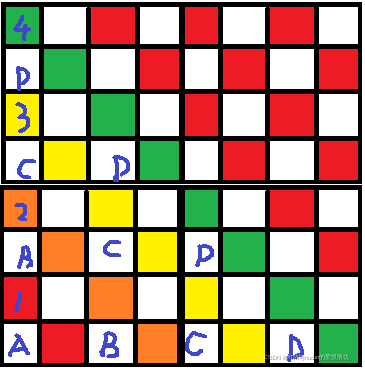
?同理,白块也可得出。
#include <bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
#define Ma 1005
#define mod 1000000007
using namespace std;
ll a[Ma][Ma];
ll n;
int main()
{
ll tt;
scanf("%lld",&tt);
while (tt--)
{
scanf("%lld",&n);
for (ll i=0;i<n;i++)
for (ll j=0;j<n;j++)
scanf("%lld",&a[i][j]);
ll ans=0,ask=0,pre=0;
for (ll i=0;i<(n-1)*2;i+=2)
{
if (i<n)
for (ll j=0;j<=i;j+=2)
ask^=a[i-j][j];
else
for (ll j=n-1;j>=0&&i-j<n;j-=2)
ask^=a[i-j][j];
ans^=pre^ask;
pre^=ask;
ask=0;
}
ask=0,pre=0;
for (ll i=(n-1);i>-(n-1);i-=2)
{
if (i>0)
for (ll j=0;j<n&&i+j<n;j+=2)
ask^=a[i+j][j];
else
for (ll j=n-1;j>=0&&i+j>=0;j-=2)
ask^=a[i+j][j];
ans^=pre^ask;
pre^=ask;
ask=0;
}
printf("%lld\n",ans);
}
return 0;
}F1. Game on Sum (Easy Version)(dp+数学+概率+博弈)
这题题目意思很简单,就是让Alice选数,让bob判断状态,bob一定不想让Alice更高,因此他指挥选择b场加分场,我们可以假设x=b为加分的场数,y=a-b为减分的场数,我们定义dp[i][j]为赢i场,输j场所得的最大分。
对于j=0,Alice一定选择k,因此dp[i][0]=k*i;
对于dp[i][j](j>0),我们假设Alice选择q为得分,则dp[i][j]=min(dp[i-1][j]+q,dp[i][j-1]-q)
而max dp[i][j]=(dp[i-1][j]+dp[i][j-1])/2,因此可用dp得出
复杂度o(n*m)
#include <bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
#define Ma 2005
#define mod 1000000007
using namespace std;
ll dp[Ma][Ma];
ll po(ll p,ll x=mod-2)
{
ll sum=1;
while (x)
{
if (x&1)
sum*=p,sum%=mod;
p*=p,p%=mod;
x>>=1;
}
return sum;
}
int main()
{
ll tt;
scanf("%lld",&tt);
dp[0][0]=0;
for (ll i=1;i<Ma;i++)
for (ll j=0;j<Ma;j++)
if (j==0)
dp[i][j]=(dp[i-1][j]+1);
else
dp[i][j]=(dp[i-1][j]+dp[i][j-1])*po(2)%mod;
while (tt--)
{
ll a,b,c;
scanf("%lld%lld%lld",&a,&b,&c);
printf("%lld\n",dp[b][a-b]);
}
return 0;
}F2. Game on Sum (Hard Version)(数学+递推)
上面我们得出了dp[i][j]=(dp[i-1][j]+dp[i][j-1])/2,对于x=4,y=2的情况我们可以写出其状态
我们发现除去i=0/j=0的情况其余都以二项分布形式展开(因为i=0/j=0时并不进行传递了)
因此我们可以用dp[i][1]的状态进行转移其分数概率,而对于我们的移动情况来说,转移至dp[i][0]的概率为dp[i][1],因此可以得出答案。

#include <bits/stdc++.h>
#define ll long long
#define ls p<<1
#define rs p<<1|1
#define Ma 2000005
#define mod 1000000007
using namespace std;
ll mul[Ma],pre[Ma];
ll mi[Ma];
ll po(ll p,ll x=mod-2)
{
ll sum=1;
while (x)
{
if (x&1)
sum*=p,sum%=mod;
p*=p,p%=mod;
x>>=1;
}
return sum;
}
void pri()
{
mul[0]=pre[0]=mi[0]=1;
for (ll i=1;i<Ma;i++)
mul[i]=mul[i-1]*i%mod,pre[i]=po(mul[i]),mi[i]=mi[i-1]*po(2)%mod;
return;
}
ll C(ll x,ll y)
{
if (x>y||x<0||y<0)
return 0;
return mul[y]*pre[x]%mod*pre[y-x]%mod;
}
int main()
{
pri();
ll tt;
scanf("%lld",&tt);
while (tt--)
{
ll a,b,c;
scanf("%lld%lld%lld",&a,&b,&c);
ll ans=0;
swap(a,b);
b-=a;
if (b==0)
ans=a;
else
for (ll i=0;i<a;i++)
ans=(ans+C(i,i+b-1)*mi[b+i]%mod*(a-i)%mod)%mod;
printf("%lld\n",ans*c%mod);
}
return 0;
}?