开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> JavaScript知识库 -> JS：二叉堆 3题、区间问题 7 题 -> 正文阅读

[JavaScript知识库]JS：二叉堆 3题、区间问题 7 题

小顶堆

其他语言可以用优先队列完成小顶堆的功能，但没有内置函数的JavaScript就要手写一个小顶堆。面试题要用，起码可以复制一个没错的数据结构。如果要求手写小顶堆，我们也可以从理解上记忆。

之前写过的 23.合并K个升序链表（困难）JS代码

小顶堆（优先队列）有两个主要 API，分别是 insert 插入一个元素和 delMin 删除最小元素。

二叉堆可用数组实现，核心是父节点与左右子节点有倍数关系。一步步构建

类的数据结构和获取节点（索引）（要熟悉JS怎么写类）

class minHeap {
    constructor(){
        this.heap = []
    }
    getParent(index) {
        return Math.trunc((index - 1) / 2)
    }
    getLeft(index) {
        return index * 2 + 1
    }
    getRight(index) {
        return index * 2 + 2
    }
}

insert：把要插入的元素添加到堆底的最后（也没位置给你插了），然后让其上浮（swim）到正确位置
swim：如果某个节点 A 比它的父节点小，那么 A 不应该做子节点，应该把父节点换下来，自己去做父节点，这就是对 A 的上浮。（错位的节点 A 可能要上浮很多次，才能到达正确的位置，恢复堆的性质。所以代码中肯定有一个 while 循环。）

swim(index) {
    // 只有一个元素
    if(index == 0) return
    // 循环调整
    let parent = this.getParent(index)
    while(this.heap[parent] && this.heap[parent] > this.heap[index]) {
        this.swap(parent, index)
        // 换下来的父节点不用管, 以它为根的子树依然大于下面节点
        index = parent
        parent = this.getParent(index)
    }
}
insert(value) {
    this.heap.push(value)
    this.swim(this.heap.length - 1)
}

pop：删除元素先把堆顶元素 A 和堆底最后的元素 B 对调，然后删除 A，最后让 B 下沉到正确位置。
sink：如果某个节点 A 比它的子节点（中的一个）大，那么 A 就不配做父节点，应该下去，下面那个更小的节点上来做父节点，这就是对 A 进行下沉。

sink(index) {
    // 下沉某个节点A，需要A和其两个子节点比较大小
    let left = this.getLeft(index)
    while(left < this.heap.length) {
        let right = this.getRight(index)
        if(this.heap[right] && this.heap[right] < this.heap[left]) left = right
        if(this.heap[left] < this.heap[index]) {
            this.swap(left, index)
            index = left
            left = this.getLeft(index)
        } else {
            break // 左右子节点都大于父节点
        }
    }
}
pop(){
    if(this.heap.length == 0) return undefined
    if(this.heap.length == 1) return this.heap.shift()
    let min = this.heap[0]
    this.heap[0] = this.heap.pop()
    this.sink(0)
    return min
}

发现我上次借鉴别人的是用递归实现上浮和下沉的，这次使用循环
其余的函数

swap(p1, p2) {
    [this.heap[p1], this.heap[p2]] = [this.heap[p2], this.heap[p1]]
}
peek() {
    return this.heap[0]
}
size() {
    return this.heap.length
}

215. 数组中的第K个最大元素（中等）

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

正常思路最大元素那肯定用大顶堆，但是pop之后就不能维持（看后面一题）。而小顶堆则不需要构建大小为N的堆。
在这里插入图片描述
代码简单，主要还是实现二叉堆

var findKthLargest = function(nums, k) {
    const proir = new MinHeap()
    for(val of nums) {
        proir.insert(val)
        if(proir.size() > k) {
            proir.pop()
        }
    }
    return proir.heap[0]
};

在这里插入图片描述

这里发现小顶堆代码有小瑕疵

295. 数据流的中位数（困难）

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。
设计一个支持以下两种操作的数据结构：
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。

参考文章，如果数据规模非常巨大，排序不太现实
在这里插入图片描述

本题的核心思路是使用两个优先级队列。
一个大顶堆或小顶堆，它的中位数都在二叉树的中间某一层。
让大顶堆管理小的那一部分，每次出的数都是（低层次）最大的。
让小顶堆管理大的那一部分，每次出的数都是（高层次）最小的。
只要保证两个堆数量相同，那么堆顶元素就是中位数。关键是保持两个堆数量相同。
想要往large里添加元素，不能直接添加，而是要先往small里添加，然后再把small的堆顶元素加到large中；向small中添加元素同理。

这里就通过变量控制小顶堆还是大顶堆

var MedianFinder = function() {
    this.minqueue = new PriorQueue('min') // 高位数
    this.maxqueue = new PriorQueue('max') // 低位数
};

/** 
 * @param {number} num
 * @return {void}
 */
MedianFinder.prototype.addNum = function(num) {
    // 优先放高位数
    if(this.minqueue.size() != this.maxqueue.size()) { // 说明低位数少
        this.minqueue.insert(num)
        this.maxqueue.insert(this.minqueue.pop())
    } else {
        this.maxqueue.insert(num)
        this.minqueue.insert(this.maxqueue.pop())
    }
    // console.log(this.minqueue.heap)
    // console.log(this.maxqueue.heap)
};

/**
 * @return {number}
 */
MedianFinder.prototype.findMedian = function() {
    if(this.minqueue.size() == this.maxqueue.size()) {
        return (this.minqueue.peek() + this.maxqueue.peek()) / 2
    } else {
        return this.minqueue.peek()
    }
};

问题所在：我还以为逻辑错误，弄了一个小时。

我一直使用this.heap[right]和this.heap[parent]来判断是否越界，可惜没考虑到，元素的值可以为0。之前没有错，是因为元素为一个对象。
再严谨一点Math.trunc((index - 1) / 2)，因为-0.5会变成0

应该改为

parent>=0
right<this.heap.length
Math.floor((index-1)/2)

在这里插入图片描述

最终的完全正确的小顶堆和大顶堆代码

class PriorQueue {
    constructor(mark) {
        this.heap = []
        this.mark = mark
    }
    getParent(index) {
        return Math.floor((index-1)/2)
    }
    getLeft(index) {
        return index * 2 + 1
    }
    getRight(index) {
        return index * 2 + 2
    }
    compare(p, cur) {
        if(this.mark=='min') {
            return p > cur
        } else {
            return p < cur
        }
    }
    swim(index) {
        if(index==0) return
        let parent = this.getParent(index)
        while(parent>=0 && this.compare(this.heap[parent], this.heap[index])) {
            this.swap(parent, index)
            index = parent
            parent = this.getParent(index)
        }
    }
    insert(val) {
        this.heap.push(val)
        this.swim(this.heap.length-1)
    }
    sink(index) {
        let left = this.getLeft(index)
        while(left < this.heap.length) {
            let right = this.getRight(index)
            if(right<this.heap.length && this.compare(this.heap[left], this.heap[right])) left = right
            if(this.compare(this.heap[index], this.heap[left])) {
                this.swap(left, index)
                index = left
                left = this.getLeft(index)
            } else {
                break
            }
        }
    }
    pop() {
        if(this.heap.length == 0) return undefined
        if(this.heap.length == 1) return this.heap.shift()
        let min = this.heap[0]
        this.heap[0] = this.heap.pop()
        this.sink(0)
        return min
    }
    swap(p1, p2) {
        [this.heap[p1], this.heap[p2]] = [this.heap[p2], this.heap[p1]]
    }
    peek() {
        return this.heap[0]
    }
    size() {
        return this.heap.length
    }
}

703. 数据流中的第 K 大元素（简单）

设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。

因为每当加入一个数后，就返回第K大的元素，说明二叉堆里面存放的是最大的K个数。使用小顶堆来维持。使用修改后的小顶堆：

var KthLargest = function(k, nums) {
    this.k = k
    this.minqueue = new PriorQueue('min')
    for (val of nums) this.minqueue.insert(val)
};

/** 
 * @param {number} val
 * @return {number}
 */
KthLargest.prototype.add = function(val) {
    this.minqueue.insert(val)
    while(this.minqueue.size() > this.k) this.minqueue.pop()
    return this.minqueue.peek()
};

区间问题

在这里插入图片描述

主要有两个技巧：
在这里插入图片描述
排序的思想：应用在了信封嵌套问题

1288. 删除被覆盖区间（中等）fail

给你一个区间列表，请你删除列表中被其他区间所覆盖的区间。
只有当 c <= a 且 b <= d 时，我们才认为区间 [a,b) 被区间 [c,d) 覆盖。
在完成所有删除操作后，请你返回列表中剩余区间的数目。

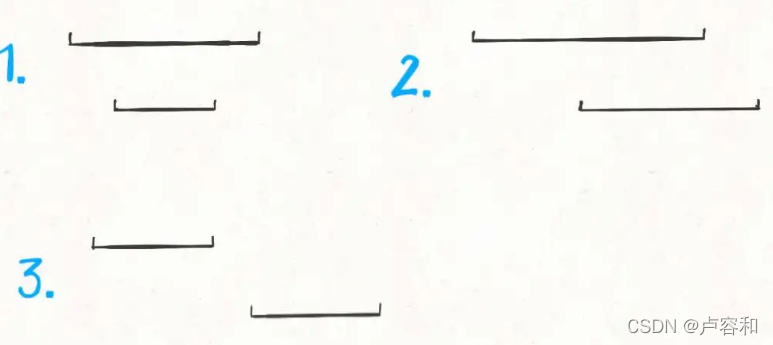
在这里插入图片描述

在这里插入图片描述
文章列举了三种情况，但实际只需考虑两种：覆盖和不能覆盖。
因为起点是递增的，考虑完当前元素，下一个肯定是往右开始的。如果不覆盖，我们需要的是更大的终点，而起点只是顺带的。

var removeCoveredIntervals = function(intervals) {
    intervals.sort((a, b) => {return a[0]==b[0] ? b[1]-a[1] : a[0] - b[0] })
    let st = intervals[0][0], en = intervals[0][1], count = 0
    for (let i = 1; i < intervals.length; i++) {
        if(st <= intervals[i][0] && en >= intervals[i][1]) {
            count++
        } else {
            st = intervals[i][0]
            en = intervals[i][1]
        }
    }
    return intervals.length - count;
};

难度还是：为什么要对终点降序排列
对于这两个起点相同的区间，我们需要保证长的那个区间在上面（按照终点降序），这样才会被判定为第一个覆盖第二个。否则会被错误地判定为相交（不覆盖），然后更新终点

var removeCoveredIntervals = function(intervals) {
    intervals.sort((a, b) => {return a[0]==b[0] ? b[1]-a[1] : a[0] - b[0] })
    let en = intervals[0][1], count = 0
    for (let i = 1; i < intervals.length; i++) {
        if(en >= intervals[i][1]) {
            count++
        } else {
            en = intervals[i][1]
        }
    }
    return intervals.length - count;
};

56. 合并区间（中等）

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

还是排序操作
这题就要考虑相交情况了。

var merge = function(intervals) {
    intervals.sort((a, b) => {return a[0]==b[0] ? b[1]-a[1] : a[0]-b[0] })
    let st = intervals[0][0], en = intervals[0][1], ans = []
    for(let i=1; i<intervals.length; i++) {
        // 内含
        if(st<=intervals[i][0] && en>=intervals[i][1]) continue
        // 相交
        if(en>=intervals[i][0] && en<=intervals[i][1]) {
            en = intervals[i][1]
        }
        // 不相交
        if(en < intervals[i][0]) {
            ans.push([st, en])
            st = intervals[i][0]
            en = intervals[i][1]
        }
    }
    // 还剩一组
    ans.push([st, en])
    return ans;
};

文章这里只对起点排序，因为它合并了覆盖和相交这两种情况。
只有重叠和不相交。（en >= intervals[i][0]和en < intervals[i][0]）

57. 插入区间（中等） fail

给你一个无重叠的，按照区间起始端点排序的区间列表。
在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

把每个区间与新区间比较
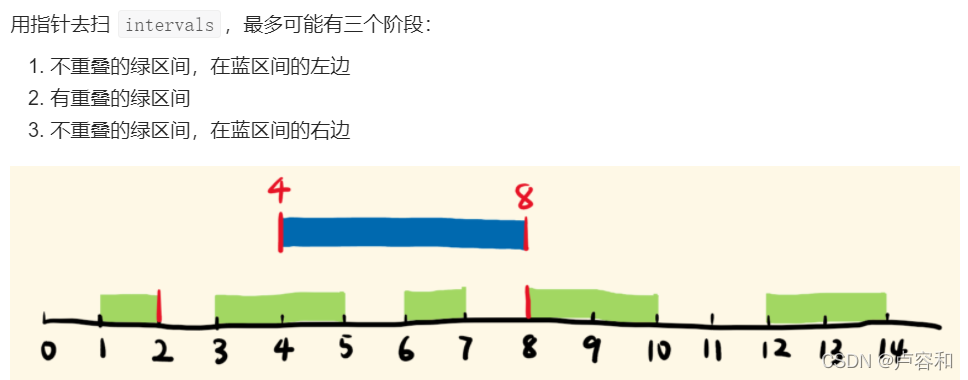
在这里插入图片描述

能做对，关键是要明白绿色新区间从进入蓝色区间到出来蓝色区间的条件。而我只盯着蓝色区间的两端，并没有一个滑动的概念。
在这里插入图片描述

var insert = function(intervals, newInterval) {
    let res = [], i = 0, len = intervals.length
    // 新区间的左侧
    while(i < len && intervals[i][1]<newInterval[0]) {
        res.push(intervals[i])
        i++
    }
    // 相交或内含
    while(i<len && intervals[i][0]<=newInterval[1]) {
        newInterval[0] = Math.min(intervals[i][0], newInterval[0])
        newInterval[1] = Math.max(intervals[i][1], newInterval[1])
        i++
    }
    res.push(newInterval)
    while(i<len) {
        res.push(intervals[i])
        i++
    }
    return res;
};

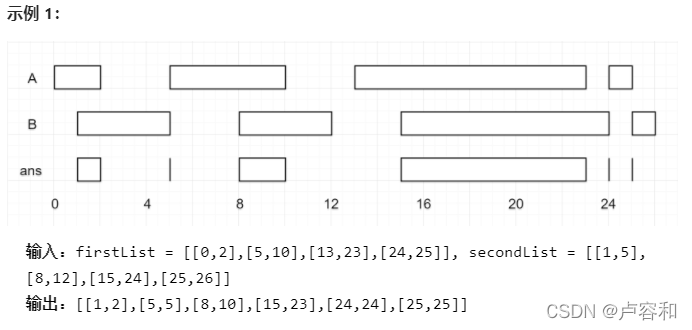
986. 区间列表的交集（中等）

虽然在数组里做过，但明显是知道要考虑什么情况下才会做。所以再独立做一次。

两个闭区间的交集是一组实数，要么为空集，要么为闭区间。例如，[1, 3] 和 [2, 4] 的交集为 [2, 3] 。

相交的情况：4种
不相交情况：2种
比较完，移动谁？看终点，较前的，比较完，就用不着了。

var intervalIntersection = function(firstList, secondList) {
    let i = 0, j = 0, res = [];
    while (i<firstList.length && j<secondList.length) {
        let [a1, a2] = firstList[i], [b1, b2] = secondList[j]
        // 没有交集
        if(a2 < b1 || a1 > b2) {
            a2 < b2 ? i++ : j++
            continue
        }
        // 有交集
        if(a2 >= b1 && a1 <= b2) {
            res.push([Math.max(a1, b1), Math.min(a2, b2)])
        }
        // 保留更远的
        a2 < b2 ? i++ : j++
    }
    return res
};

区间调度问题（贪心算法）

在这里插入图片描述

435. 无重叠区间（中等）

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回需要移除区间的最小数量，使剩余区间互不重叠。

至少需要移除几个区间？反过来说就是区间中最多有几个互不相交的区间。

var eraseOverlapIntervals = function(intervals) {
    if(intervals.length == 0) return 0
    intervals.sort((a, b) => {return a[1] - b[1]})
    let i = 1, end = intervals[0][1], count = 1
    for(; i<intervals.length; i++) {
        if(intervals[i][0] < end) continue
        count++
        end = intervals[i][1]
    }
    return intervals.length - count
};

452. 用最少数量的箭引爆气球（中等）

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend，且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。
给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

这题就是找重叠最多。其实稍微思考一下，这个问题和区间调度算法一模一样。——如果最多有 n 个不重叠的区间，那么就至少需要 n 个箭头穿透所有区间
在这里插入图片描述
把>=换成>

var findMinArrowShots = function(points) {
    points.sort((a, b) => {return a[1] - b[1]})
    let count = 1, i = 1, end = points[0][1]
    for(; i < points.length; i++) {
        if(points[i][0] > end) {
            // 找到下一个选择的区间了
            count++
            end = points[i][1]
        }
    }
    return count
};

1024. 视频拼接（中等）fail

使用数组 clips 描述所有的视频片段，其中 clips[i] = [starti, endi] 表示：某个视频片段开始于 starti 并于 endi 结束。
甚至可以对这些片段自由地再剪辑：
例如，片段 [0, 7] 可以剪切成 [0, 1] + [1, 3] + [3, 7] 三部分。
我们需要将这些片段进行再剪辑，并将剪辑后的内容拼接成覆盖整个运动过程的片段（[0, time]）。返回所需片段的最小数目，如果无法完成该任务，则返回 -1 。

给定一个目标区间和若干小区间，如何通过裁剪和组合小区间拼凑出目标区间？最少需要几个小区间？

在这里插入图片描述
重点：因为视频不能断开，只能从重叠中选出终点最长的区间
为什么要逆序，因为第一个区间一定要选最长的

我是预选选择了第一个区间作为开始

var videoStitching = function(clips, time) {
    clips.sort((a, b) => { return a[0]==b[0] ? b[1]-a[1] : a[0]-b[0]})
    if(clips[0][0] != 0) return -1
    if(clips[0][1] >= time) return 1
    let res = 1, i = 1, curEnd = clips[0][1], nextEnd = 0
    while(i < clips.length && clips[i][0] <= curEnd) {
        while(i < clips.length && clips[i][0] <= curEnd) {
            nextEnd = Math.max(nextEnd, clips[i][1])
            i++
        }
        // 下一个区间不重叠
        res++
        // 使用重叠且最远的区间
        curEnd = nextEnd
        if(curEnd >= time) return res
    }
    // 重叠最远的区间达不到
    return -1
};

也可以通过初始化curEnd = 0，即要求第一个区间一定要<=curEnd=0
这样只要保证选择下一个区间的终点是最远就不需要逆序排列。（第二个while循环的作用）

var videoStitching = function(clips, time) {
    clips.sort((a, b) => { return a[0]-b[0]})
    let res = 0, i = 0, curEnd = 0, nextEnd = 0
    while(i < clips.length && clips[i][0] <= curEnd) {
        while(i < clips.length && clips[i][0] <= curEnd) {
            nextEnd = Math.max(nextEnd, clips[i][1])
            i++
        }
        // 下一个区间不重叠
        res++
        // 使用重叠且最远的区间
        curEnd = nextEnd
        if(curEnd >= time) return res
    }
    // 重叠最远的区间达不到
    return -1
};