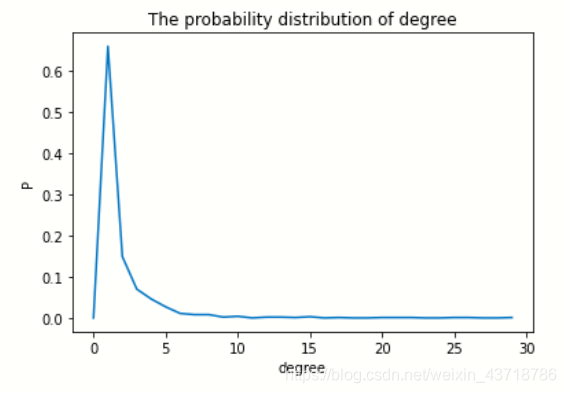
用简洁的python代码生成无标度网络,并绘制网络度的分布
假设有如下一个简单网络
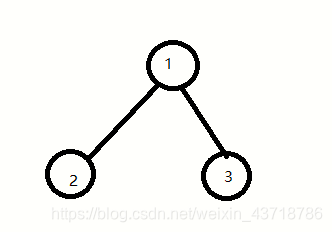
网络的邻接矩阵和度数如下
| ------- | node 1 | node 2 | node 3 | degree |
|---|---|---|---|---|
| node 1 | -------- | 1 | 1 | 2 |
| node 2 | 1 | ----- | 0 | 1 |
| node 3 | 1 | 0 | 0 | 1 |
假设一个新的点4要和这三个点进行连接
- 和点1、2、3连接的概率分别是: 3 3 + 2 + 2 \frac{3}{3+2+2} 3+2+23?、 2 3 + 2 + 2 \frac{2}{3+2+2} 3+2+22?、 2 3 + 2 + 2 \frac{2}{3+2+2} 3+2+22?
- 把这三个概率加在一起为1
- 那可以使用一个随机数,看落在三段的那一段里,来判断和对应的哪个点发生连接
思路是嵌套循环+随机数+if条件判断
- 第一层循环,每次循环代表一个新生成的点
- 第二层循环(内层),每次循环代表判断是否和这个点产生连接
生成一个平均度为 2 n ? 1 2 \frac{2n-1}{2} 22n?1?的网络,具体代码如下
import numpy as np
nodes_degree = []
N = 1000 # 生成1000个点
link = []
for i in range(N):
link.append([])
for i in range(N): # i为每一个点,进行连接
nodes_degree = [int(np.sum(node))+1 for node in link]
p = np.random.randint(np.sum(nodes_degree))
degree_control = 0
for j, degree in enumerate(nodes_degree):
if p < degree_control:
link[i].append(j)
link[j].append(i)
break
else:
degree_control += degree
绘制网络度的分布
import matplotlib.pyplot as plt
mxdeg=0
for i in range(N):
mxdeg=max(mxdeg,link[i].__len__())
mxdeg+=1
deg=[0]*mxdeg
for i in range(N):
deg[link[i].__len__()]+=1
for i in range(mxdeg):
deg[i]/=1.0*N
plt.plot(np.linspace(0,mxdeg-1,mxdeg),deg)
plt.xlabel('degree')
plt.ylabel('P')
plt.title('The probability distribution of degree')
plt.show()
度的分布: