递归

文章目录

递归

何为递归？

递归是一种解决问题的方法，将问题分解为更小的子问题，直到得到一个足够小的问题可以被很简单的解决。

通常递归涉及函数调用自身。

递归允许我们编写优雅的解决方案，解决可能很难编程的问题。

初探递归：列表求和问题 1 + 3 + 5 + 7 + 9

1：我们的常规思路

((((1 + 3) + 5) + 7) + 9)

2：当然可以变换一下思维

(1 + (3 + (5 + (7 + 9))))

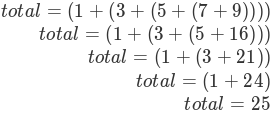
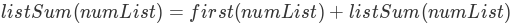
3：自然而然就形成了递归公式在这里插入图片描述

在这里插入图片描述

# 将问题分解为更小的子问题，直到得到一个足够小的问题可以被很简单的解决。
# 通常递归涉及函数调用自身。
# 递归允许我们编写优雅的解决方案，解决可能很难编程的问题。

# 计算整数列表和，一般方法
def get_sum(list_number):
    answer = 0
    for i in list_number:
        answer = answer + i
    return answer

# 计算整数列表和，递归方法
def get_sum2(list_number):
    # 特殊情况的终止
    if len(list_number) == 0:
        return -1
    # 终止条件，只剩下一个的时候
    if len(list_number) == 1:
        return list_number[0]
    # get_sum2(list_number) = list_number[0] + get_sum2(list_number[1: ])
    else:
        return list_number[0] + get_sum2(list_number[1: ]) # 递归调用


if __name__ == "__main__":
    test_list_number = [1, 3, 5, 7, 9]
    print(get_sum(test_list_number))
    print(get_sum2(test_list_number))

递归三部曲：斐波那契数列到思考三部曲

假设一对刚出生的小兔一个月后就能长成大兔，再过一个月就能生下一对小兔，并且此后每个月都生一对小兔，一年内没有发生死亡，那么一对刚出生的兔子，在一年内繁殖成多少对兔子?

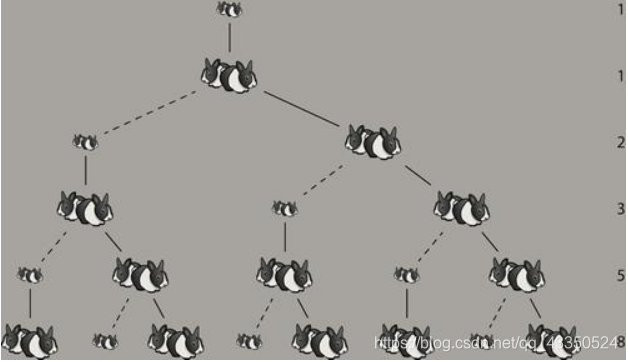
在这里插入图片描述

第一步：递归函数的功能是什么

# 假设函数的功能是求n个月后兔子的数量
def getRabbit(month):

第二步：找出递归的结束条件

# 显然 month = 1时为1对兔子，month = 2时为1对兔子
def getRabbit(month):
    if month <= 2:
        return 1

第三步：找出函数的等价关系式

这一步是最为重要，也是最为复杂的一步。

分析一下：

本月的兔子的个数 = 本月的大兔子个数 + 本月的小兔子个数

而

? 本月的大兔子个数 = 上月的小兔子的个数 + 上月的大兔子个数【上月大兔子不死】= 上月的所有的兔子

? 本月的小兔子个数 = 上月大兔子新生的 = 上上月的小兔子的个数 + 上上月的大兔子个数【不死且生新的】= 上上月的所有的兔子

∴ 本月的兔子个数 = 上月的兔子的个数 + 上上月的兔子个数【F(n) = F(n - 1) + F(n - 2)】

# getrRabbit(month) = getRabbit(month - 1) + getRabbit(month - 2)
def getRabbit(month):
    if month <= 2:
        return 1
    else:
        return getRabbit(month - 1) + getRabbit(month - 2)

为什么上述结束条件找的是两个月，而不是一个月，三个月?

结束条件的个数问题就要从函数的等价关系式中找到答案了：就是等价关系式和几个”前世“有关系 = 几个结束条件的个数

如斐波那契数列中等价关系式为：F(n) = F(n - 1) + F(n - 2)，和上一个和上上一个有关，所以最少需要两个月作为结束条件才可以，否则，如果只以month == 1时作为结束条件，则F(2) = F(2 - 1) + F(2 - 2)你的通式就不成立了，而如果将month == 3时的结果也作为结束条件的一部分，就是浪费了：因为F(3) = F(3 - 1) + F(3 - 2) = F(2) + F(1)是完全可以计算的，多写只会徒增工作，有时还会算错

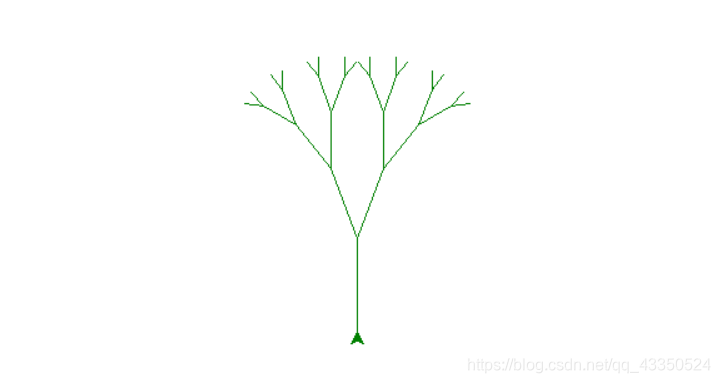
可视化递归：海龟turtle

import turtle
def tree(branchLen,t):
    if branchLen > 5:
        t.forward(branchLen)
        t.right(20)
        tree(branchLen-15,t) # 右转15%执行递归
        t.left(40)
        tree(branchLen-15,t) # 右转15%执行递归
        t.right(20)
        t.backward(branchLen)
def main():
    t = turtle.Turtle()
    myWin = turtle.Screen()
    t.left(90)
    t.up()
    t.backward(100)
    t.down()
    t.color("green")
    tree(75,t)
    myWin.exitonclick()
main()

在这里插入图片描述

更高级一些的：艾宾浩斯三角形

阐明了三路递归算法。用手绘制谢尔宾斯基三角形的过程很简单。

1：从一个大三角形开始。通过连接每一边的中点，将这个大三角形分成四个新的三角形。

2：忽略刚刚创建的中间三角形，对三个小三角形中的每一个应用相同的过程。

3：每次创建一组新的三角形时，都会将此过程递归应用于三个较小的角三角形。

import turtle
def drawTriangle(points,color,myTurtle):
    myTurtle.fillcolor(color)
    myTurtle.up()
    myTurtle.goto(points[0][0],points[0][1])
    myTurtle.down()
    myTurtle.begin_fill()
    myTurtle.goto(points[1][0],points[1][1])
    myTurtle.goto(points[2][0],points[2][1])
    myTurtle.goto(points[0][0],points[0][1])
    myTurtle.end_fill()
def getMid(p1,p2):
    return ( (p1[0]+p2[0]) / 2, (p1[1] + p2[1]) / 2)
def sierpinski(points,degree,myTurtle):
    colormap = ['blue','red','green','white','yellow',
                'violet','orange']
    drawTriangle(points,colormap[degree],myTurtle)
    if degree > 0:
        sierpinski([points[0],
                        getMid(points[0], points[1]),
                        getMid(points[0], points[2])],
                   degree-1, myTurtle)
        sierpinski([points[1],
                        getMid(points[0], points[1]),
                        getMid(points[1], points[2])],
                   degree-1, myTurtle)
        sierpinski([points[2],
                        getMid(points[2], points[1]),
                        getMid(points[0], points[2])],
                   degree-1, myTurtle)
def main():
   myTurtle = turtle.Turtle()
   myWin = turtle.Screen()
   myPoints = [[-100,-50],[0,100],[100,-50]]
   sierpinski(myPoints,3,myTurtle)
   myWin.exitonclick()
main()

在这里插入图片描述

其他例子

青蛙跳台阶

普通青蛙

一只青蛙一次可以跳一级台阶，也可以一次跳两级台阶，现在有 n 级台阶，问青蛙一共有多少种跳法？

解题思路

我们先令 f(n) 为 n 级台阶的总跳法数，那么第一次如果选择跳一级的话，那么剩下的 n-1 级台阶的跳法数就为 f(n-1)，如果第一次跳两级的话，那么剩下的 n-2 级台阶的跳法就是 f(n-2)，然后再回到题目中要求来看，青蛙一次只能挑一级或两级，也就是说刚刚列举的这两种情况的和就是青蛙一共有多少种跳法，所以 f(n) = f(n-1) + f(n-2) = 斐波那契数列算法通式。

def jumpCount(steps):
    if steps <= 2:
        return steps # 1阶 = 1种跳法, 2阶 = 2种跳法
    else:
        return jumpCount(steps - 1) + jump(step - 2)

变态青蛙

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

解题思路

首次跳1阶,方式即为剩下的n-1阶f(n-1)；首次跳2阶，方式即为f(n-2)；首次3阶方式为f(n-3)，依次…即：

f(n) = f(n-1) + f(n-2) + f(n-3) + …f(2) + f(1);

而同理：

f(n-1) = f(n-2) + f(n-3) + …f(2) + f(1)

代入上式即得：
f(n) = 2 * f(n-1) = 2^(n - 1)

可以看成每一个台阶都有两种可能，跳或者不跳，所以是2 的N 次方，但是最后一个台阶是必须跳的，所以是2的n-1次方

class Solution:
    def jumpFloor2(self, number):
        # write code here
        sum = pow(2,(number-1))
        return sum

汉诺塔

一块黄铜板上插着三根宝石针。印度教的主神在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

解决思路

如果A柱子只剩一个盘子，那么直接移动到C柱子即可
把 n-1 号盘子移动到缓冲区
把1号从起点移到终点
然后把缓冲区的n-1号盘子也移到终点

def moveTower(height,fromPole, toPole, withPole):
    if height >= 1:
        moveTower(height-1,fromPole,withPole,toPole)
        moveDisk(fromPole,toPole)
        moveTower(height-1,withPole,toPole,fromPole)