[Python知识库]向量的三重积公式及其证明（附python代码）

向量的三重积公式是经常会在向量代数中使用到的恒等式，它的表达形式如下所示：$$a\times \left(b\times c\right)=\left(a?c\right)b?\left(a?b\right)c$$

我们可以使用以下python代码来进行证明（我们对上式稍微变形一下证明这个恒等式即可）$$a\times \left(b\times c\right)?\left(a?c\right)b+\left(a?b\right)c=0$$

import sympy as sym
from sympy import sin,cos,diff

x_a,y_a,z_a,x_b,y_b,z_b,x_c,y_c,z_c = sym.symbols('x_a,y_a,z_a,x_b,y_b,z_b,x_c,y_c,z_c')
a = sym.Matrix([x_a,y_a,z_a])
b = sym.Matrix([x_b,y_b,z_b])
c = sym.Matrix([x_c,y_c,z_c])

A = a.cross(b.cross(c))
B = a.dot(c)*b
C = a.dot(b)*c

print(sym.simplify(A-B+C))

输出的结果为：

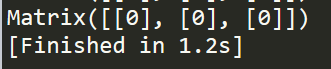
可见，这个恒等式是成立的。
当然，我们也可以手动计算，计算量稍微大一点，需要耐心和仔细。

利用三重积公式，我们可以得到另外一个有趣的恒等式，即：
$$a\times \left(b\times c\right)+b\times \left(c\times a\right)+c\times \left(a\times b\right)=0$$

我们也可以直接使用python程序进行证明：

import sympy as sym
from sympy import sin,cos,diff

x_a,y_a,z_a,x_b,y_b,z_b,x_c,y_c,z_c = sym.symbols('x_a,y_a,z_a,x_b,y_b,z_b,x_c,y_c,z_c')
a = sym.Matrix([x_a,y_a,z_a])
b = sym.Matrix([x_b,y_b,z_b])
c = sym.Matrix([x_c,y_c,z_c])

A = a.cross(b.cross(c))
B = b.cross(c.cross(a))
C = c.cross(a.cross(b))

print(sym.simplify(A+B+C))

输出的结果为：

可见，这个恒等式是成立的。
当然，我们也可以手动计算，直接利用三重积公式展开然后合并同类项即可。