[Python知识库]【数据挖掘】通过两点的经纬度高效计算实际的地球球面距离

由于地球是存在弧度的，所以在已知两点经纬度的情况下直接计算直线距离在一些场景下并不可取的，在计算过程中需要考虑到地球赤道半径等参数，从而得到真实的地球球面距离。在这里将一些计算方法记录下来，方便之后作为工具直接调用。

1. 仅使用math库进行距离计算直线距离

def get_distance_function(latA, lonA, latB, lonB):
    ra = 6378140  # 赤道半径
    rb = 6356755  # 极半径
    flatten = (ra - rb) / ra  # Partial rate of the earth
    # change angle to radians
    radLatA = math.radians(latA)
    radLonA = math.radians(lonA)
    radLatB = math.radians(latB)
    radLonB = math.radians(lonB)

    pA = math.atan(rb / ra * math.tan(radLatA))
    pB = math.atan(rb / ra * math.tan(radLatB))
    x = math.acos(math.sin(pA) * math.sin(pB) + math.cos(pA) * math.cos(pB) * math.cos(radLonA - radLonB))
    c1 = (math.sin(x) - x) * (math.sin(pA) + math.sin(pB)) ** 2 / math.cos(x / 2) ** 2
    c2 = (math.sin(x) + x) * (math.sin(pA) - math.sin(pB)) ** 2 / math.sin(x / 2) ** 2
    dr = flatten / 8 * (c1 - c2)
    distance = ra * (x + dr)
    distance = round(distance / 1000, 4)
    # return f'{distance}km'
    return distance

2. 调用geopy库进行直线距离计算

from geopy.distance import geodesic

print(geodesic((latA, lonA), (latB, lonB)).m)
print(geodesic((latA, lonA), (latB, lonB)).km)

3. 调用geopy库进行球面距离计算

from geopy.distance import great_circle

print(great_circle((latA, lonA), (latB, lonB)).km)

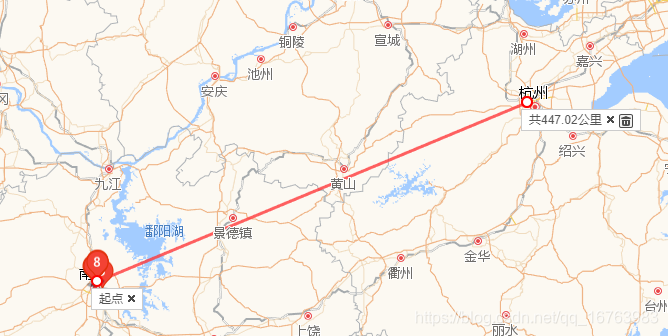
最后对不同的计算方法进行实际数值测试并验证正确性：

latA = 30.28708
lonA = 120.12802999999997
latB = 28.7427
lonB = 115.86572000000001

print(get_distance_function(latA, lonA, latB, lonB))

print(geodesic((latA, lonA), (latB, lonB)).km)

print(great_circle((latA, lonA), (latB, lonB)).km)

得到的结果分别是：

447.2498
447.2497993542003
446.72135807011483

除此之外，geopy还有其他实用功能，概括如下（之后再开拓）：

• 地理编码：将字符串转换为地理位置
• 逆地理编码：用于将地理坐标转换为具体地址
• 计算两个点的距离：经纬度距离和球面距离

有关geopy的安装，这里不再赘述，方法和安装其他库是一样的，总的来说就是conda/pip+可能会换镜像源。如果都不能成功安装，那就直接使用万能的方法，在Unofficial Windows Binaries for Python Extension Packages中搜索下载，然后在本地pip install即可。需要注意的是确定好平台支持版本（pip debug --verbose可查看），参考我之前写的一篇文章：如何下载安装whl轮子以及确定Python适配版本

参考资料：

• 根据经纬度坐标计算距离-python
• geopy在python中的使用
• Python经纬度坐标转换为距离及角度的实现