学习目标
理解偏差与方差
学会运用学习曲线找到最好的模型
1,拟合数据
首先,我们将所有的数据分成三部分,训练集(60%),测试集(20%)和交叉验证集(20%)。
import scipy.io as scio
import numpy as np
import scipy.optimize as opt
import matplotlib.pyplot as plt
def load_data():
d = scio.loadmat('ex5data1.mat')
return map(np.ravel, [d['X'], d['y'], d['Xval'], d['yval'], d['Xtest'], d['ytest']])
X, y, Xval, yval, Xtest, ytest = load_data()
def cost(theta, X, y):
m = X.shape[0] # m=12
inner = X @ theta - y # R(m*1),X(12,2),theta(2,1)
square_sum = inner.T @ inner
cost = square_sum / (2 * m)
return cost
def gradient(theta, X, y): # 梯度,cost的导数
m = X.shape[0] # 12
inner = X.T @ (X @ theta - y) # (m,n).T @ (m, 1) -> (n, 1)
return inner / m
def regularized_gradient(theta, X, y, l=1):
m = X.shape[0]
regularized_term = theta.copy() # 直接赋值会让两个变量指向一个值
regularized_term[0] = 0 # don't regularize intercept theta
regularized_term = (l / m) * regularized_term
return gradient(theta, X, y) + regularized_term
def regularized_cost(theta, X, y, l=1):
m = X.shape[0]
regularized_term = (l / (2 * m)) * np.power(theta[1:], 2).sum()
return cost(theta, X, y) + regularized_term
def linear_regression_np(X, y, l=1):
theta = np.ones(X.shape[1])
res = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient,
options={'disp': True})
return res
theta = np.ones(X.shape[1])
final_theta = linear_regression_np(X, y, l=0).get('x')
b = final_theta[0] # intercept
m = final_theta[1] # slope
plt.scatter(X[:,1], y, label="Training data")
plt.plot(X[:, 1], X[:, 1]*m + b, label="Prediction")
plt.legend(loc=2)
plt.show()
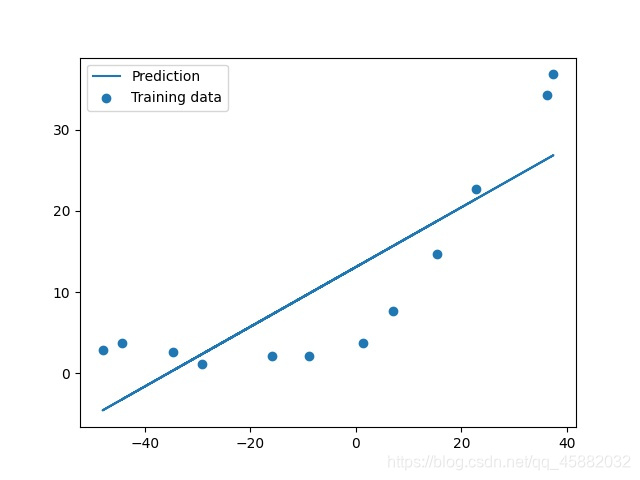
显然用直线拟合数据效果并不好,我们看一下训练数据从1到12的损失函数和交叉损失。
training_cost, cv_cost = [], []
m = X.shape[0] # m =12
for i in range(1, m + 1):
res = linear_regression_np(X[:i, :], y[:i], l=0)
tc = regularized_cost(res.x, X[:i, :], y[:i], l=0)
cv = regularized_cost(res.x, Xval, yval, l=0)
training_cost.append(tc)
cv_cost.append(cv)
plt.plot(np.arange(1, m+1), training_cost, label='training cost')
plt.plot(np.arange(1, m+1), cv_cost, label='cv cost')
plt.legend(loc=1)
plt.show()
2,画出学习曲线
在i=1时,只用一个数据来计算tc(training cost)和cv(cross validation),显然由于只有一个数据点tc应该为0。i = 2,时由于两点确定一条直线,所以tc也为0.当数据越来越多时,直线并不能很好的拟合即欠拟合了。
具体情况如图:
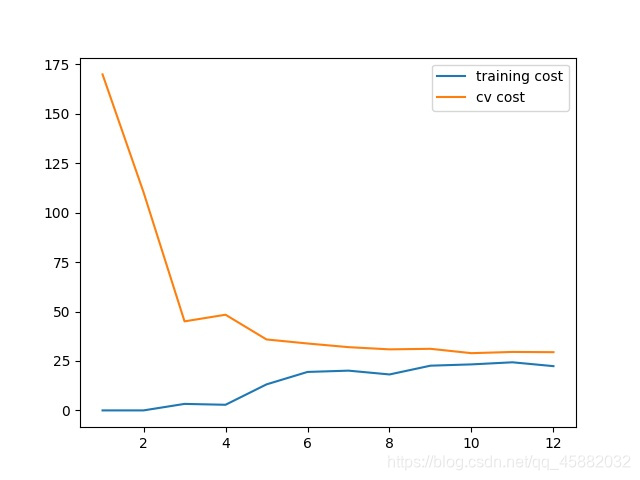
显然用直线并不能很好的拟合数据,用老办法,我们将数据映射到高维。(创建多项式特征)
def poly_features(x, power, as_ndarray=False):
data = {'f{}'.format(i): np.power(x, i) for i in range(1, power + 1)} # 将x拓展为x,x^2,x^3
df = pd.DataFrame(data)
return df.values if as_ndarray else df
当然映射到高维会使数据差距巨大,特征缩放必然是少不了的。
def normalize_feature(df): # 特征缩放
return df.apply(lambda column: (column - column.mean()) / column.std()) # lambda函数:前为输入,:后为输出
最后整合一下这两个函数
def prepare_poly_data(*args, power):
def prepare(x):
# expand feature
df = poly_features(x, power=power) # 将特征向高维拓展
# normalization
ndarr = normalize_feature(df).values
# add intercept term
return np.insert(ndarr, 0, np.ones(ndarr.shape[0]), axis=1)
return [prepare(x) for x in args]
现在可以再次画出学习曲线了。
X_poly, Xval_poly, Xtest_poly = prepare_poly_data(X, Xval, Xtest, power=8) # 所有数据集拓展
plot_learning_curve(X_poly, y, Xval_poly, yval, l=0)
plt.show()

看起来还可以,但训练集的损失函数一直为0,或许有些过拟合。
3,找到最佳的𝜆
要想找到最佳的λ,就是要找到交叉验证集的损失最小的模型。通常情况下我们为你让lambda=[0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]来寻找最优解
l_candidate = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
training_cost, cv_cost = [], []
for l in l_candidate:
res = linear_regression_np(X_poly, y, l)
tc = cost(res.x, X_poly, y)
cv = cost(res.x, Xval_poly, yval)
training_cost.append(tc)
cv_cost.append(cv)
plt.plot(l_candidate, training_cost, label='training')
plt.plot(l_candidate, cv_cost, label='cross validation')
plt.legend(loc=2)
plt.xlabel('lambda')
plt.ylabel('cost')
plt.show()

显而易见,λ的值等于1时交叉验证集的损失函数最小(也可使用l_candidate[np.argmin(cv_cost)],输出结果为1),最后我们找到了最佳的λ值。