前言
我先吐槽一下,学习这个库使用的难点有很多,这是个用的很少的库,资料很少,只能看官方文档(cvxpy库的官方文档),而官方文档是全英文,给同学们造成了很大的困扰!首先,安装它就是个挺费劲的事情,我当时装了1天(cvxpy库的安装),我自己写了个安装的方法。其次,函数看不懂,不知道在干啥,资料又查不到,所以我在学了1天,有了个浅显的了解之后,便写了这篇文章
在了解这个库如何使用之前,必须必须要了解pandas,numpy的数组的操作,否则你也看不懂!
一、运输问题
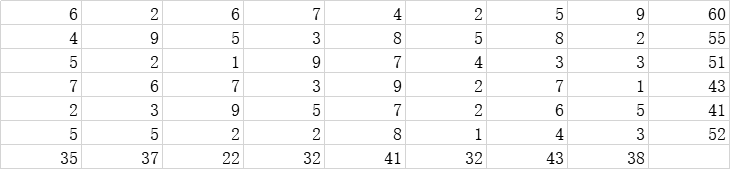
已知某种商品6个仓库的存货量,8个客户对该商品的需求量,单位商品运价如表所示,试确定6个仓库到8个客户的商品调运数量,使总的运输费用最小
import cvxpy as cp
import numpy as np
import pandas as pd
d1=pd.read_excel("C:\\Users\\86189\\Desktop\\technology\\python执行文件\\数学建模\\线性规划\\单位商品运价.xlsx",header=None)#读excel
d2=d1.values#将读取到的数据转化为数组的形式
c=d2[:-1,:-1]#-1是最后一个元素的索引值,end=-1意思就是除了最后一个元素不包含,其他都包含
d=d2[-1,:-1].reshape(1,-1)
#意思:从行来看,最后一行;从列来看,除了最后一列不取其他都取
#reshape表明转变为1行,-1的意思是列数自己计算
e=d2[:-1,-1].reshape(-1,1)#与上面同理
x=cp.Variable([6,8])#生成6行8列的变量
obj=cp.Minimize(cp.sum(cp.multiply(c,x)))
#构造目标函数obj。字面意思理解,multiply是两个矩阵相乘,sum是求和,minimize就是最小值
con=[cp.sum(x,axis=1,keepdims=True)<=e,cp.sum(x,axis=0,keepdims=True)==d,x>=0]
#三个约束条件,关于sum的使用我放在下面
prob=cp.Problem(obj,con)
prob.solve(solver='GLPK_MI',verbose=True)
#用GLPKMI解决问题,verbose=True表明显示具体求解信息
print('最优值为:',prob.value)
print('最优解为:\n',x.value)
1.首先要先自己创建excel表格,明白c,d,e的意思;
x=cp.Variable([6,8])意思是生成6行8列的变量,注意,是变量!相当于说,创建一个矩阵,里面全是变量的矩阵,我们所求的就是这个矩阵里的所有变量!
2.区别:实际上在numpy中也有sum,multiply函数,
一位博主做的关于numpy.sum的使用,类比cvxpy库即可
但是与cvxpy最大的不同是,numpy中的函数是需要知道矩阵的具体信息的;而cvxpy的函数可以包含矩阵未知量,求解未知量。
就好比小学时候学的方程求解:
对于numpy:6*3=18
对于cvxpy:6x=18解得x=3
就是这两个库同名函数的区别所在
3.详细注释已经打在上面了,如果没明白的话可以讨论讨论
求解结果:
D:\Anaconda\python.exe "C:/Users/86189/Desktop/technology/python执行文件/数学建模/线性规划/运输问题模型 司守奎例5.2.3.py"
===============================================================================
CVXPY
v1.1.13
===============================================================================
(CVXPY) Jul 16 10:40:12 PM: Your problem has 48 variables, 3 constraints, and 0 parameters.
(CVXPY) Jul 16 10:40:12 PM: It is compliant with the following grammars: DCP, DQCP
(CVXPY) Jul 16 10:40:12 PM: (If you need to solve this problem multiple times, but with different data, consider using parameters.)
(CVXPY) Jul 16 10:40:12 PM: CVXPY will first compile your problem; then, it will invoke a numerical solver to obtain a solution.
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
(CVXPY) Jul 16 10:40:12 PM: Compiling problem (target solver=GLPK_MI).
(CVXPY) Jul 16 10:40:12 PM: Reduction chain: Dcp2Cone -> CvxAttr2Constr -> ConeMatrixStuffing -> GLPK_MI
(CVXPY) Jul 16 10:40:12 PM: Applying reduction Dcp2Cone
(CVXPY) Jul 16 10:40:12 PM: Applying reduction CvxAttr2Constr
(CVXPY) Jul 16 10:40:12 PM: Applying reduction ConeMatrixStuffing
(CVXPY) Jul 16 10:40:12 PM: Applying reduction GLPK_MI
(CVXPY) Jul 16 10:40:12 PM: Finished problem compilation (took 6.321e-03 seconds).
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
(CVXPY) Jul 16 10:40:12 PM: Invoking solver GLPK_MI to obtain a solution.
0: obj = 1.114000000e+03 inf = 2.280e+02 (1)
13: obj = 1.347000000e+03 inf = 0.000e+00 (0)
* 31: obj = 6.640000000e+02 inf = 0.000e+00 (0)
Long-step dual simplex will be used
+ 31: mip = not found yet >= -inf (1; 0)
+ 31: >>>>> 6.640000000e+02 >= 6.640000000e+02 0.0% (1; 0)
+ 31: mip = 6.640000000e+02 >= tree is empty 0.0% (0; 1)
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
(CVXPY) Jul 16 10:40:12 PM: Problem status: optimal
(CVXPY) Jul 16 10:40:12 PM: Optimal value: 6.640e+02
(CVXPY) Jul 16 10:40:12 PM: Compilation took 6.321e-03 seconds
(CVXPY) Jul 16 10:40:12 PM: Solver (including time spent in interface) took 9.589e-04 seconds
最优值为: 664.0
最优解为:
[[-0. 19. -0. -0. 41. -0. -0. -0.]
[-0. -0. -0. 32. -0. -0. -0. 1.]
[-0. 12. 22. -0. -0. -0. 17. -0.]
[-0. -0. -0. -0. -0. 6. -0. 37.]
[35. 6. -0. -0. -0. -0. -0. -0.]
[-0. -0. -0. -0. -0. 26. 26. -0.]]
Process finished with exit code 0