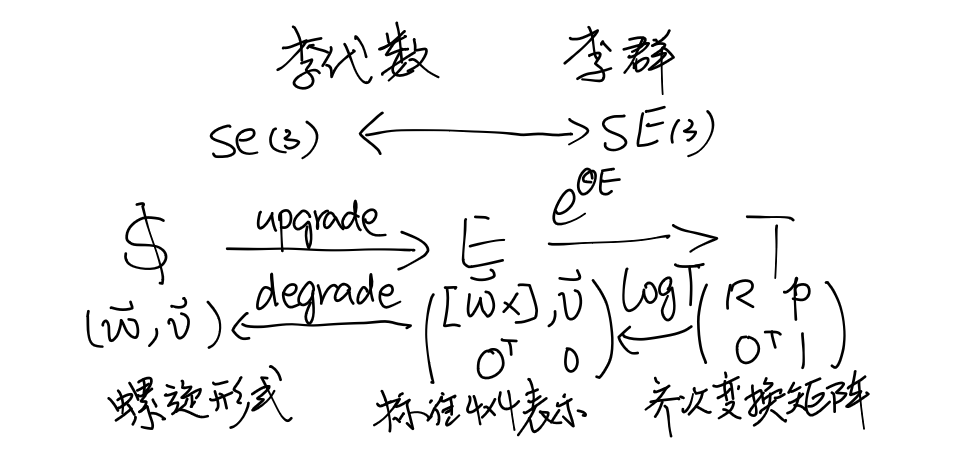
SE(3)李群和se(3)李代数元素之间存在着指对数的映射关系(矩阵指数、对数运算关系),对于se(3)李代数,存在着向量形式(六维螺旋向量S)和4×4标准矩阵(E矩阵)两种表达,他们之间可以相互转换,我们把从S转换成E的过程称为升维(upgrade),把E转换为S的过程称为降维(upgrade),那么我们可以简单地得到以下的转换关系示意图:
李代数se(3)的螺旋向向量形式和标准4×4表示之间的转换关系比较简单,只需要对其中的角速度向量做一个伴随(反对称)变换即可,然后反对称矩阵和速度向量进行拼接,然后最后一行拼上全零向量就可以得到一个4×4的矩阵E。从E到T,我们可以用多种方法,比如采用罗德里格斯公式、引入G变换、直接使用logm等,这里使用最简单的logm函数进行数值计算进行验证。我们可以看到,从S到E再到T,然后从T回到E和S,最终的计算结果形成了一个闭环,说明我们的程序和理论都是正确的。
import numpy as np
from scipy.linalg import expm,logm
from numpy import pi,sin,cos,tan,arccos,matmul
from numpy.linalg import norm
# from robotools import Euler_Rodrigues,SE3tose3
np.set_printoptions(precision=3,suppress=True)
deg = pi/180
def vec2sM(vec):
return np.array([
[0,-vec[2],vec[1]],
[vec[2],0,-vec[0]],
[-vec[1],vec[0],0]
])
def sM2vec(sM):
return np.array([sM[2][1],sM[0][2],sM[1][0]])
def upgradeStoE(Screw):
'''
规定:Screw=(S,S0),单位旋量screw=(s,s0),Screw=theta*screw
规定:omg为三维的单位向量,OMG = theta*omg,
把运动旋量Screw∈se(3),转换(升维)成T的矩阵对数E矩阵
#E=Eu*theta,其中theta为转角,Eu为单位螺旋对应的矩阵对数
'''
theta = norm(Screw[:3])
screw = Screw.reshape((6,1))/theta
omg,vel = screw[:3],screw[-3:]
sMomg = vec2sM(omg)
bottom = np.array([[0,0,0,0]])
Eu = np.r_[np.c_[sMomg,vel],bottom]
return Eu.astype(float)*theta
def degradeEtoS(Ematrix):
'''
输入:李代数的4×4标准表示E矩阵
输出:对应的李代数向量形式Screw
'''
sMOMG = Ematrix[:3,:3]
VEL = Ematrix[:3,3].reshape(3,1)
OMG = sM2vec(sMOMG).reshape(3,1)
theta = np.linalg.norm(OMG)
omg = OMG/theta
vel = VEL/theta
screw = np.vstack((omg,vel))
# sMomg = sMOMG/theta
# Ginv = 1/theta*I-1/2*sMomg+(1/theta-0.5/tan(theta/2))*np.matmul(sMomg,sMomg)
return (screw*theta).reshape(1,6)
s = np.array([0,0,1,3.37,-3.37,0])
theta = pi/6
Twist = s*theta
E = upgradeStoE(Twist)
T = expm(E)
EM = logm(T)
Screw = degradeEtoS(EM)
print(f"Twist={Twist}")
print(f"E={E}")
print(f"T={T}")
print(f"EM ={EM}")
print(f"Screw={Screw}")