对策论

简介：对策论亦称竞赛论或博弈论。参加斗争或竞争的各方各自具有不同的目标和利益。为了达到各自的目标和利益，各方必须考虑对手的各种可能的行动方案，并力图选取对自己最为有利或最为合理的方案。对策论就是研究对策行为中斗争各方是否存在着最合理的行动方案，以及如何找到这个合理的行动方案的数学理论和方法。

对策的基本要素

（i）局中人:在一个对策行为（或一局对策）中，有权决定自己行动方案的对策参加者，称为局中人。
（ii）策略集：一局对策中，可供局中人选择的一个实际可行的完整的行动方案称为一个策略。一般，每一局中人的策略集中至少应包括两个策略。
（iii）赢得函数（支付函数）：在一局对策中，各局中人所选定的策略形成的策略组称为一个局势。

零和对策（矩阵对策）

零和对策：零和对策是一类特殊的对策问题。在这类对策中，只有两名局中人，每个局中人都只有有限个策略可供选择。在任一纯局势下，两个局中人的赢得之和总是等于零，即双方的利益是激烈对抗的。
在这里插入图片描述
求解思想：由于两个人的对策是权衡的，所以一个人的决策对自己越有利，则对另一个人越有害，两个人都在寻找一个中心策略，使两个人都不会坏到极致，所以只需要考虑自己做的每种决策中，自己选的决策下对面最优解（即自己最差解）的情况视为选择该策略的最差结果，然后得到的每种策略下的最差结果中最优解为对自己最有利的选择。
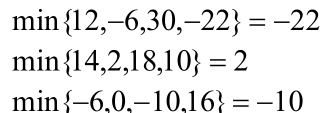
在这里插入图片描述

零和矩阵最后所得的数一定是所在行和所在列中，最大和最小的数，若在所在行最大，则在所在列最小。反之亦然。