[Python知识库]python手写光线追踪（不使用图形学API）——第三期

本文未经允许禁止转载
B站：https://space.bilibili.com/455965619
作者：Heskey0 / 赫斯基皇

三.lambertian材质的半球采样

因为lambertian材质涉及到的知识比较多，所以单独用一章进行讲解
在本章中，我会讲解漫反射的一部分知识：

1.cosine hemisphere sampling

2.计算lambertian材质的漫反射法线方向和pdf

我们要实现对球面的uniform sampling，可以先在圆盘中采样

1. 在一个正方形中采样
2. 将点转换到一个圆，并且用极坐标表示
3. 将圆上的点映射到半球

(1) concentric sample

我们先对正方形进行均匀采样

    x = ti.random() * 2.0 - 1.0
    y = ti.random() * 2.0 - 1.0

在上述代码中，x和y均为 -1 ~ 1，这样采样到的点是连续的。

然后，我们使用concentric sample的方式将(x,y)从笛卡尔坐标系中的正方形映射到极坐标系中的圆
即：(x,y) => (r,θ)

我们具体代码的实现：

    if x != 0 or y != 0:
        if abs(x) > abs(y):
            r = x
            theta = np.pi / 4 * (y / x)
        else:
            r = y
            theta = np.pi / 4 * (2 - x / y)

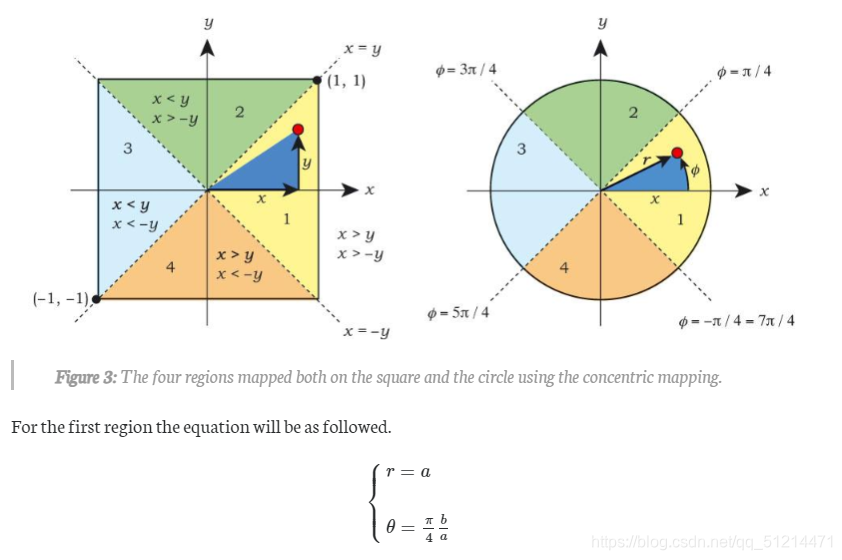
那么，为何不直接使用高中学的 坐标变换公式

即：
$$\{\begin{array}{l}r=\sqrt{x^2+y^2}\\ \theta =arctan(\frac{y}{x})\end{array}$$

注意： 我们的目的是uniform sampling，而平方，开方，$arctan()$ 破坏了(x,y)的线性关系。
（$\theta =\frac{\pi }{4}?\frac{b}{a}$虽然使用了除法，但当a不变时，$\theta$依然是连续的）

(2) Malley’s method

然后，我们需要将点(r,φ)（即上面的(r,θ)）从极坐标系映射到球坐标系
即： (r,φ) => (θ,φ)

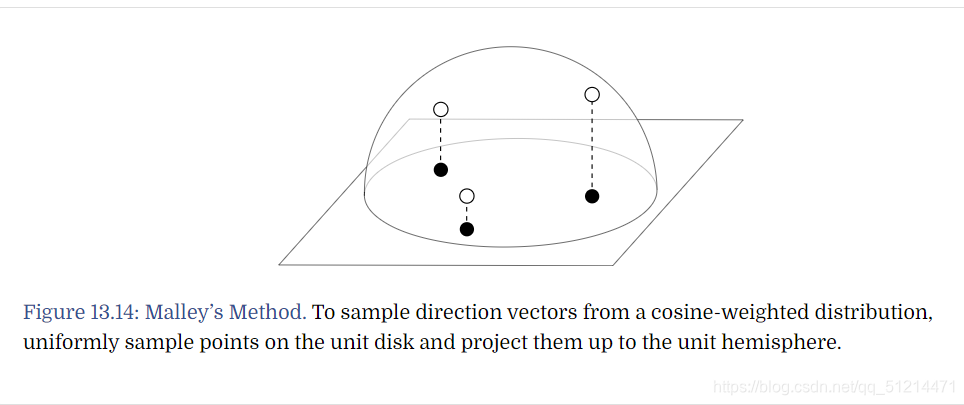
原理有些复杂，我们先看代码：

    # 1
    u = ti.Vector([1.0, 0.0, 0.0])
    if abs(normal[1]) < 1 - eps:
        u = normal.cross(ti.Vector([0.0, 1.0, 0.0]))
    v = normal.cross(u)
	# 2
    xy = r*ti.cos(phi)*u + r*ti.sin(phi)*v
    zlen = ti.sqrt(max(0.0, 1.0 - xy.dot(xy)))

    return xy + zlen * normal       # 反射光的方向

我们先看u和v的作用

1. 不需要关心normal和vector.up的关系，vector.up的引入是为了 辅助建立起坐标系 (u,v,normal)
2. 从计算中可以看出：u,v垂直, 长度均为sin(phi), 均 在微平面上
3. 由 normal为中心轴 , u和v为水平轴 建立笛卡尔坐标系

这里插一句：要表示一个法线(x,y,z)的方向，我们只需要两个数据：(x,y)。因为，我们可以通过 $z=\sqrt{1?x^2?y^2}$ 计算出z的值。

代码中的xy其实就是在(u,v)平面中的一个向量，我们根据 $z=\sqrt{1?x^2?y^2}$ 求出z的长度值。注意：我们的运算不是在(x,y,z)坐标系中进行的，而是在(u,v,normal)坐标系中。所以，我们的求出的z长度值还要乘以normal向量。

返回值为漫反射材质表面的法线（u）

最后，根据此法线（u），可以求出pdf的值

	pdf = max(0.0001, normal.dot(u) / np.pi)

normal为垂直于材质表面的法线，u为计算出漫反射的法线
注意：normal和u均为单位向量，上面代码等价于：
$pdf=\frac{\cos (?)}{\pi }$ [$?$为u与normal的夹角]