[Python知识库]【Python】DS的基础学习笔记10：Numpy库

Numpy库

10.1 为什么要用Numpy

10.1.1 低效的Python for循环

【例】求100万个数的倒数

def compute_reciprocals(values):
    res = []
    for value in values:  # 每遍历一个元素，就要判断其类型，并查找适用于该数据类型的正确函数
        res.append(1/value)
    return res


values = list(range(1, 1000000))
%timeit compute_reciprocals(values)

145ms ± 13.7ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

%timeit：ipython中统计运行时间的魔术方法（多次运行取平均值）

import numpy as np

values = np.arange(1, 1000000)
%timeit 1/values

5.99 ms ± 33.9 $\mu$s per loop (mean ± std. dev. of 7 runs, 100 loops each)

实现相同计算，Numpy的运行速度是Python循环的25倍，产生了质的飞跃

10.1.2 Numpy为什么如此高效

Numpy 是由C语言编写的

1. 编译型语言 VS 解释型语言
   C语言执行时，对代码进行整体编译，速度更快

2. 连续单一类型存储 VS 分散多变类型存储
   （1）Numpy数组内的数据类型必须是统一的，如全部是浮点型，而Python列表支持任意类型数据的填充
   （2）Numpy数组内的数据连续存储在内存中，而Python列表的数据分散在内存中
   这种存储结构与一些更加高效的底层处理方式更加契合

3. 多线程 VS 线程锁
   Python语言执行时有线程锁，无法实现多线程并行，而C语言可以

10.1.3 什么时候用Numpy

在数据处理的过程中，遇到使用“Python for循环”实现一些向量化、矩阵化操作的时候，要优先考虑Numpy

如：1.两个向量点乘
　　2.矩阵乘法

10.2 Numpy数组的创建

10.2.1 从列表开始创建

import numpy as np

x = np.array([1, 2, 3, 4, 5])
print(x)
print(type(x))
print(x.shape)

[1 2 3 4 5]
<class ‘numpy.ndarray’>
(5,)

• 设置数组的数据类型

x = np.array([1, 2, 3, 4, 5], dtype="float32")
print(x)
print(type(x[0]))

[1. 2. 3. 4. 5.]
<class ‘numpy.float32’>

• 二维数组

x = np.array([[1, 2, 3],
             [4, 5, 6],
             [7, 8, 9]])
print(x)
print(x.shape)

[[1 2 3]
[4 5 6]
[7 8 9]]
(3, 3)

10.2.2 从头创建数组

1. 创建长度为5的数组，值都为0

x = np.zeros(5, dtype=int)
print(x)

[0 0 0 0 0]

2. 创建一个2*4的浮点型数组，值都为1

x = np.ones((2, 4), dtype=float)
print(x)

[[1. 1. 1. 1.]
[1. 1. 1. 1.]]

3. 创建一个3*5的数组，值都为8.8

x = np.full((3, 5), 8.8)
print(x)

[[8.8 8.8 8.8 8.8 8.8]
[8.8 8.8 8.8 8.8 8.8]
[8.8 8.8 8.8 8.8 8.8]]

4. 创建一个3*3的单位矩阵

x = np.eye(3)
print(x)

[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]

5. 创建一个线性序列数组，从1开始，到15结束，步长为2

x = np.arange(1, 15, 2)
print(x)

[ 1 3 5 7 9 11 13]

6. 创建一个4个元素的数组，这四个数均匀的分配到0~1

x = np.linspace(0, 1, 4)
print(x)

[0. 0.33333333 0.66666667 1. ]

7. 创建一个10个元素的数组，形成1~10^9的等比数列

x = np.logspace(0, 9, 10)
print(x)

[1.e+00 1.e+01 1.e+02 1.e+03 1.e+04 1.e+05 1.e+06 1.e+07 1.e+08 1.e+09]

8. 创建一个3*3的，在0~1之间均匀分布的随机数构成的数组

x = np.random.random((3, 3))
print(x)

[[0.24071227 0.07969712 0.63823522]
[0.35498076 0.9118258 0.15769803]
[0.99262848 0.4967521 0.83731092]]

9. 创建一个3*3的，均值为0，标准差为1的正态分布随机数构成的数组

x = np.random.normal(0, 1, (3, 3))
print(x)

[[-0.72929168 2.17232632 0.14290452]
[-0.40683984 -1.13513294 -1.99699889]
[ 1.10233893 -2.028775 1.31215984]]

10. 创建一个3*3的，在[0, 10]之间随机整数构成的数组

x = np.random.randint(0, 10, (3, 3))
print(x)

[[9 8 6]
[5 2 3]
[4 3 6]]

11. 随机重排列

x = np.array([10, 20, 30, 40])
y = np.random.permutation(x)  # 生产新列表
print(y)
print(x)  # 并没有修改原列表
np.random.shuffle(x)  # 修改原列表
print(x)

[40 30 20 10]
[10 20 30 40]
[10 40 30 20]

12. 随机采样

• 按指定形状采样

x = np.arange(10, 25, dtype=float)
print(x)

[10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24.]

x = np.arange(10, 25, dtype=float)
y = np.random.choice(x, size=(4, 3))
print(y)

[[19. 12. 17.]
[12. 18. 13.]
[15. 21. 20.]
[16. 21. 12.]]

• 按概率采样

y = np.random.choice(x, size=(4, 3), p=x/np.sum(x))
print(y)

[[11. 20. 18.]
[13. 24. 11.]
[15. 10. 14.]
[22. 21. 20.]]

10.3 Numpy数组的性质

10.3.1 数组的属性

x = np.random.randint(10, size=(3, 4))
print(x)

[[1 7 5 2]
[7 8 0 4]
[0 0 5 5]]

1 数组的形状 shape

print(x.shape)

(3, 4)

2 数组的维度 ndim

print(x.ndim)

2

y = np.arange(10)
print(y.ndim)

1

3 数组的大小 size

print(x.size)

12

4 数组的数据类型 dtype

print(x.dtype)

int32

10.3.2 数组的索引

1 一维数组的索引

x1 = np.arange(10)
print(x1)
print(x1[0])
print(x1[5])
print(x1[-1])

[0 1 2 3 4 5 6 7 8 9]
0
5
9

2 多维数组的索引——以二维为例

x2 = np.random.randint(0, 20, (2, 3))
print(x2)
print(x2[0, 0])
print(x2[1][1])

[[ 2 2 11]
[ 9 6 11]]
2
6

注意：Numpy数组的数据类型是固定的，向一个整型数组插入一个浮点值，浮点值会向下进行取整

x2[1, 2] = 1.618
print(x2[1, 2])

1

10.3.3 数组的切片

1 一维数组——和列表一样

x1 = np.arange(10)
print(x1)
print(x1[:3])
print(x1[3:])
print(x1[::-1])

[0 1 2 3 4 5 6 7 8 9]
[0 1 2]
[3 4 5 6 7 8 9]
[9 8 7 6 5 4 3 2 1 0]

2 多维数组——以二维为例

x2 = np.random.randint(20, size=(3, 4))
print(x2)
print(x2[:2, :3])  # 前两行，前三列
print(x2[:2, 0:3:2])  # 前两行，前三列（每隔一列）
print(x2[::-1, ::-1])

[[ 8 19 6 4]
[ 7 1 5 4]
[12 0 9 7]]
[[ 8 19 6]
[ 7 1 5]]
[[8 6]
[7 5]]
[[ 7 9 0 12]
[ 4 5 1 7]
[ 4 6 19 8]]

3 获取数组的行和列

x3 = np.random.randint(20, size=(3, 4))
print(x3)
print(x3[1, :])  # 第一行，从0开始计数
print(x3[1])  # 第一行缩写
print(x3[:, 2])  # 第二列，从0开始计数

[[ 2 4 2 8]
[13 12 7 5]
[ 9 4 18 19]]
[13 12 7 5]
[13 12 7 5]
[ 2 7 18]

4 切片获取的是视图，而非副本

x4 = np.random.randint(20, size=(3, 4))
print(x4)
x5 = x4[:2, :2]
print(x5)
x5[0, 0] = 0  # 视图元素发生修改，原数组亦发生相应修改
print(x4)
print(x5)

[[ 5 16 9 8]
[13 19 4 5]
[13 11 17 12]]
[[ 5 16]
[13 19]]
[[ 0 16 9 8]
[13 19 4 5]
[13 11 17 12]]
[[ 0 16]
[13 19]]

注意：视图元素发生修改，则原数组亦发生相应修改

修改切片的安全方式：copy

x4 = np.random.randint(20, size=(3, 4))
print(x4)
x6 = x4[:2, :2].copy()  # 切片安全模式
print(x6)
x6[0, 0] = 0
print(x4)  # 原数组并未变化
print(x6)

[[ 4 10 19 5]
[16 2 2 5]
[17 7 14 13]]
[[ 4 10]
[16 2]]
[[ 4 10 19 5]
[16 2 2 5]
[17 7 14 13]]
[[ 0 10]
[16 2]]

10.3.4 数组的变形

x5 = np.random.randint(0, 10, (12,))
print(x5)
print(x5.shape)

[9 3 4 2 0 3 4 9 1 3 0 1]
(12,)

x6 = x5.reshape(3, 4)
print(x6)

[[9 3 4 2]
[0 3 4 9]
[1 3 0 1]]

注意：reshape返回的是视图，而非副本

x6[0, 0] = 0
print(x5)

[0 3 4 2 0 3 4 9 1 3 0 1]

一维向量转行向量

x7 = x5.reshape(1, x5.shape[0])
print(x7)

[[9 3 4 2 0 3 4 9 1 3 0 1]]

x8 = x5[np.newaxis, :]
print(x8)

[[9 3 4 2 0 3 4 9 1 3 0 1]]

一维向量转列向量

x7 = x5.reshape(x5.shape[0], 1)
print(x7)

[[9]
[3]
[4]
[2]
[0]
[3]
[4]
[9]
[1]
[3]
[0]
[1]]

x8 = x5[:, np.newaxis]
print(x8)

[[9]
[3]
[4]
[2]
[0]
[3]
[4]
[9]
[1]
[3]
[0]
[1]]

多维向量转一维向量

x6 = np.random.randint(0, 10, (3, 4))
print(x6)

[[3 5 0 9]
[9 6 1 2]
[2 4 1 2]]

flatten返回的是副本

x9 = x6.flatten()
print(x9)

[3 5 0 9 9 6 1 2 2 4 1 2]

x9[0] = 0
print(x6)

[[3 5 0 9]
[9 6 1 2]
[2 4 1 2]]

x6并未发生变化

ravel返回的是视图

x10 = x6.ravel()
print(x10)
x10[0] = 0
print(x6)

[3 5 0 9 9 6 1 2 2 4 1 2]
[[0 5 0 9]
[9 6 1 2]
[2 4 1 2]]

reshape返回的是视图

x11 = x6.reshape(-1)
print(x11)
x11[0] = 0
print(x6)

[3 5 0 9 9 6 1 2 2 4 1 2]
[[0 5 0 9]
[9 6 1 2]
[2 4 1 2]]

10.3.5 数组的拼接

x1 = np.array([[1, 2, 3], 
               [4, 5, 6]])
x2 = np.array([[7, 8, 9],
               [0, 1, 2]])

1 水平拼接——非视图

x3 = np.hstack([x1, x2])
print(x3)

[[1 2 3 7 8 9]
[4 5 6 0 1 2]]

注意为非视图，对x3的修改对原数组无变化，是一个副本

x3[0][0] = 0
print(x1)

[[1 2 3]
[4 5 6]]

另外一种方法为np.c_[ ]

x4 = np.c_[x1, x2]
print(x4)

[[1 2 3 7 8 9]
[4 5 6 0 1 2]]

同样地，该x4也是一个副本，对此修改对原数组无影响

x4[0][0] = 0
print(x1)

[[1 2 3]
[4 5 6]]

2 垂直拼接——非视图

x1 = np.array([[1, 2, 3],
               [4, 5, 6]])
x2 = np.array([[7, 8, 9],
               [0, 1, 2]])

x5 = np.vstack([x1, x2])
print(x5)

[[1 2 3]
[4 5 6]
[7 8 9]
[0 1 2]]

x6 = np.r_[x1, x2]
print(x6)

[[1 2 3]
[4 5 6]
[7 8 9]
[0 1 2]]

10.3.6 数组的分裂

1 split的用法

x6 = np.arange(10)
print(x6)

[0 1 2 3 4 5 6 7 8 9]

x1, x2, x3 = np.split(x6, [2, 7])  # 参数的列表为从第2个元素与第7个元素处分裂
print(x1, x2, x3)

[0 1] [2 3 4 5 6] [7 8 9]

2 hsplit的用法

x7 = np.arange(1, 26).reshape(5, 5)
print(x7)

[[ 1 2 3 4 5]
[ 6 7 8 9 10]
[11 12 13 14 15]
[16 17 18 19 20]
[21 22 23 24 25]]

left, middle, right = np.hsplit(x7, [2, 4])
print("left:\n", left)  # 第0~1列
print("middle:\n", middle)  # 第2~3列
print("right:\n", right)  # 第4列

left:
[[ 1 2]
[ 6 7]
[11 12]
[16 17]
[21 22]]
middle:
[[ 3 4]
[ 8 9]
[13 14]
[18 19]
[23 24]]
right:
[[ 5]
[10]
[15]
[20]
[25]]

3 vsplit的用法

x7 = np.arange(1, 26).reshape(5, 5)
upper, middle, lower = np.vsplit(x7, [2, 4])
print("upper:\n", upper)  # 第0~1行
print("middle:\n", middle)  # 第2~3行
print("lower:\n", lower)  # 第4行

upper:
[[ 1 2 3 4 5]
[ 6 7 8 9 10]]
middle:
[[11 12 13 14 15]
[16 17 18 19 20]]
lower:
[[21 22 23 24 25]]

10.4 Numpy四大运算

10.4.1 向量化运算

1 与数字的加减乘除等

x1 = np.arange(1, 6)
print(x1)

[1 2 3 4 5]

print("x1+5", x1+5)
print("x1-5", x1-5)
print("x1*5", x1*5)
print("x1/5", x1/5)

x1+5 [ 6 7 8 9 10]
x1-5 [-4 -3 -2 -1 0]
x1*5 [ 5 10 15 20 25]
x1/5 [0.2 0.4 0.6 0.8 1. ]

print("-x1", -x1)
print("x1**2", x1**2)
print("x1//2", x1//2)
print("x1%2", x1%2)

-x1 [-1 -2 -3 -4 -5]
x1**2 [ 1 4 9 16 25]
x1//2 [0 1 1 2 2]
x1%2 [1 0 1 0 1]

2 绝对值、三角函数、指数、对数

（1）绝对值

x2 = np.array([1, -1, 2, -2, 0])
print(abs(x2))
print(np.abs(x2))

[1 1 2 2 0]
[1 1 2 2 0]

（2）三角函数

theta = np.linspace(0, np.pi, 3)
print(theta)

[0. 1.57079633 3.14159265]

print("sin(theta)", np.sin(theta))
print("cos(theta)", np.cos(theta))
print("tan(theta)", np.tan(theta))

sin(theta) [0.0000000e+00 1.0000000e+00 1.2246468e-16]
cos(theta) [ 1.000000e+00 6.123234e-17 -1.000000e+00]
tan(theta) [ 0.00000000e+00 1.63312394e+16 -1.22464680e-16]

x = [1, 0, -1]
print("arcsin(x)", np.arcsin(x))
print("arccos(x)", np.arccos(x))
print("arctan(x)", np.arctan(x))

arcsin(x) [ 1.57079633 0. -1.57079633]
arccos(x) [0. 1.57079633 3.14159265]
arctan(x) [ 0.78539816 0. -0.78539816]

（3）指数运算

x = np.arange(3)
print(np.exp(x))

[1. 2.71828183 7.3890561 ]

（4）对数运算

x = np.array([1, 2, 4, 8, 10])
print("ln(x)", np.log(x))
print("log2(x)", np.log2(x))
print("log10(x)", np.log10(x))

ln(x) [0. 0.69314718 1.38629436 2.07944154 2.30258509]
log2(x) [0. 1. 2. 3. 3.32192809]
log10(x) [0. 0.30103 0.60205999 0.90308999 1. ]

3 两个数组的运算

x1 = np.arange(1, 6)
x2 = np.arange(6, 11)
print("x1+x2:", x1+x2)
print("x1-x2:", x1-x2)
print("x1*x2:", x1*x2)
print("x1/x2:", x1/x2)

x1+x2: [ 7 9 11 13 15]
x1-x2: [-5 -5 -5 -5 -5]
x1*x2: [ 6 14 24 36 50]
x1/x2: [0.16666667 0.28571429 0.375 0.44444444 0.5 ]

10.4.2 矩阵运算

x = np.arange(9).reshape(3, 3)
print(x)

[[0 1 2]
[3 4 5]
[6 7 8]]

• 矩阵的转置

y = x.T
print(y)

[[0 3 6]
[1 4 7]
[2 5 8]]

• 矩阵乘法

x = np.array([[1, 0],
             [1, 1]])
y = np.array([[0, 1],
             [1, 1]])

print(x.dot(y))
print(np.dot(x, y))

[[0 1]
[1 2]]
[[0 1]
[1 2]]

print(y.dot(x))
print(np.dot(y, x))

[[1 1]
[2 1]]
[[1 1]
[2 1]]

注意与x*y的区别

print(x*y)

[[0 0]
[1 1]]

对应元素相乘

10.4.3 广播运算

x = np.arange(3).reshape(1, 3)
print(x)
print(x+5)

[[0 1 2]]
[[5 6 7]]

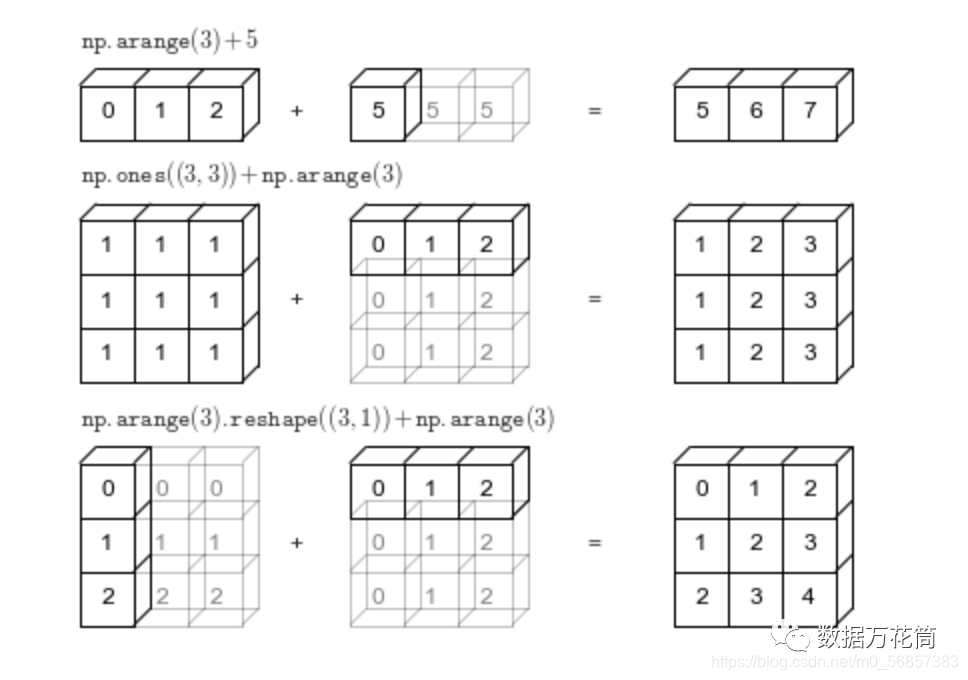
规则
如果两个数组的形状在维度上不匹配
那么数组的形式会沿着维度为1的维度进行扩展以匹配另一个数组的形状

x1 = np.ones((3, 3))
print(x1)
x2 = np.arange(3).reshape(1, 3)
print(x2)
print(x1+x2)

[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
[[0 1 2]]
[[1. 2. 3.]
[1. 2. 3.]
[1. 2. 3.]]

x3 = np.logspace(1, 10, 10, base=2).reshape(2, 5)
print(x3)
x4 = np.array([[1, 2, 4, 8, 16]])
print(x4)
print(x3/x4)

[[ 2. 4. 8. 16. 32.]
[ 64. 128. 256. 512. 1024.]]
[[ 1 2 4 8 16]]
[[ 2. 2. 2. 2. 2.]
[64. 64. 64. 64. 64.]]

x5 = np.arange(3).reshape(3, 1)
print(x5)
x6 = np.arange(3).reshape(1, 3)
print(x6)
print(x5+x6)

[[0]
[1]
[2]]
[[0 1 2]]
[[0 1 2]
[1 2 3]
[2 3 4]]

10.4.4 比较运算和掩码

1 比较运算

x1 = np.random.randint(100, size=(10, 10))
print(x1)

[[20 25 74 42 23 83 77 27 20 4]
[35 8 15 29 89 21 96 85 94 81]
[ 2 0 90 9 30 85 54 23 6 37]
[52 57 74 72 80 98 55 47 66 71]
[13 97 52 60 71 43 79 26 11 58]
[71 79 38 70 65 60 1 39 89 27]
[60 8 39 3 75 73 69 62 55 83]
[81 89 9 51 11 79 93 3 65 49]
[70 35 28 35 65 24 87 76 67 93]
[77 32 21 30 42 7 61 43 59 63]]

print(x1 > 50)

[[False False True False False True True False False False]
[False False False False True False True True True True]
[False False True False False True True False False False]
[ True True True True True True True False True True]
[False True True True True False True False False True]
[ True True False True True True False False True False]
[ True False False False True True True True True True]
[ True True False True False True True False True False]
[ True False False False True False True True True True]
[ True False False False False False True False True True]]

2 操作布尔数组

x2 = np.random.randint(10, size=(3, 4))
print(x2)

[[2 5 8 6]
[7 9 0 0]
[6 5 9 2]]

print(x2 > 5)
print(np.sum(x2 > 5))

[[False False True True]
[ True True False False]
[ True False True False]]
6

print(np.all(x2 > 0))
print(np.any(x2 == 6))
print(np.all(x2 < 8, axis=1))  # 按行进行判断，列则为0
print((x2 < 9) & (x2 > 5))
print(np.sum((x2 < 9) & (x2 > 5)))

False
True
[False False False]
[[False False True True]
[ True False False False]
[ True False False False]]
4

3 将布尔数组作为掩码

print(x2[x2 > 5])

[8 6 7 9 6 9]

通过这些布尔数组，我们很容易对数据进行处理与统计

10.4.5 花哨的索引

1 一维数组

x = np.random.randint(100, size=10)
print(x)

[82 83 93 10 16 68 38 23 38 9]

注意：结果的形状与索引数组ind一致

ind = [2, 6, 9]
print(x[ind])

[93 38 9]

ind = np.array([[1, 0],
                [2, 3]])
print(x[ind])

[[83 82]
[93 10]]

2 多维数组

x = np.arange(12).reshape(3, 4)
print(x)

[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]

row = np.array([0, 1, 2])
col = np.array([1, 3, 0])
print(x[row, col])  # x(0, 1) x(1, 3) x(2, 0)

[1 7 8]

print(row[:, np.newaxis])  # 列向量
print(x[row[:, np.newaxis], col])  # 广播机制

[[0]
[1]
[2]]
[[ 1 3 0]
[ 5 7 4]
[ 9 11 8]]

10.5 其他Numpy通用函数

10.5.1 数值排序

x = np.random.randint(20, 50, size=10)
print(x)

[44 45 37 48 47 48 48 42 30 20]

• 产生新的排序数组

print(np.sort(x))  # 产生新的排序数列
print(x)  # 不改变原数列

[20 30 37 42 44 45 47 48 48 48]
[44 45 37 48 47 48 48 42 30 20]

• 替换原数组

x.sort()  # 替换原数列
print(x)  # 改变原数列

[20 30 37 42 44 45 47 48 48 48]

• 获得排序索引

x = np.random.randint(20, 50, size=10)
print(x)
i = np.argsort(x)
print(i)

[39 23 31 48 32 30 41 47 21 24]
[8 1 9 5 2 4 0 6 7 3]

10.5.2 最大最小值

x = np.random.randint(20, 50, size=10)
print(x)
print("max:", np.max(x))
print("min:", np.min(x))
print("max_index:", np.argmax(x))
print("min_index:", np.argmin(x))

[47 33 33 39 43 33 30 24 27 40]
max: 47
min: 24
max_index: 0
min_index: 7

10.5.3 数值求和、求积

x = np.arange(1, 6)
print(x)

[1 2 3 4 5]

print(x.sum())
print(np.sum(x))

15
15

x1 = np.arange(6).reshape(2, 3)
print(x1)

[[0 1 2]
[3 4 5]]

• 按行求和

x1 = np.arange(6).reshape(2, 3)
print(np.sum(x1, axis=1))

[ 3 12]

• 按列求和

x1 = np.arange(6).reshape(2, 3)
print(np.sum(x1, axis=0))

[3 5 7]

• 求积

x = np.arange(1, 6)
print(x.prod())
print(np.prod(x))

120
120

10.5.4 中位数、均值、方差、标准差

x = np.random.normal(0, 1, size=10000)

import matplotlib.pyplot as plt


plt.hist(x, bins=50)
plt.show()

• 中位数

print(np.median(x))

-0.0038701241780846373

• 均值

print(x.mean())
print(np.mean(x))

-0.006245420694499232
-0.006245420694499232

• 方差

print(x.var())

1.0063598610872493

以上，便是第十节深入探索内容，包含Numpy的简单介绍、数组创建、数组性质、四大运算、其他函数等。
下一节将深入理解pandas库。