[Python知识库]利用Python进行数据分析笔记（随机漫步）

• 首先，让我们考虑一个简单的随机漫步，从0开始，步进为1和-1，且两种步进发生的概率相等。
• 以下是使用内建random模块利用纯Python实现的一个1000步的随机漫步：
• 以下结果是在jupyter中实现的；

import random
import matplotlib.pyplot as plt
position = 0
walk = [position]
steps = 1000
for i in range(steps):
    step = 1 if random.randint(0,1) else -1
    position += step
    walk.append(position)

• 下图是对上面随机漫步的前100步的可视化：

plt.plot(walk[:100])

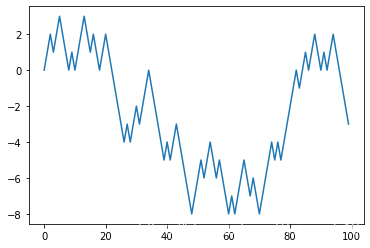
• 你可能会观察到walk只是对随机步进的累积，并且可以通过一个数组表达式实现。因此，我使用np.random模块一次性抽取1000次投掷硬币的结果，每次投掷的结果为1或-1，然后计算累计值：

nsteps = 1000
draws = np.random.randint(0,2,size=nsteps)
steps = np.where(draws > 0,1,-1)
walk = steps.cumsum()

• 由此我们开始从漫步轨道上提取一些统计数据，比如最大值、最小值等：

walk.min()
-36
walk.max()
-1

• 更复杂的统计是第一次穿越时间，即随机漫步的某一部达到了某个特定值。这里假设我们想要知道漫步中是何时连续朝某个方向连续走了10步。np.abs(walk)>=10给我们一个布尔值数组，用于表明漫步是否连续在同一方向走了十步，但是我们想要的是第一次走了10步或-10步的位置。我们可以使用argmax来计算，该函数可以返回布尔值数组中最大值的第一个位置（True就是最大值）:

(np.abs(walk) >= 10).argmax()
27

• 请注意，这里使用argmax效率并不高，因为它总是完整地扫描整个数组。在这个特殊的示例中，一旦True被发现，我们就知道最大值了。

一次性模拟多次随机漫步

• 如果你的目标是模拟多次随机漫步，比如说5000步。你可以稍微地修改下之前的代码来生成所有的随机步。如果传入一个2个元素的元组，numpy.random中的函数可以生成一个二维的抽取数组，并且我们可以一次性地跨行计算出全部5000个随机步的累积和：

nwalks = 5000
nsteps = 1000
draws = np.random.randint(0,2,size=(nwalks,nsteps)) # 0或1 详见https://blog.csdn.net/u012474716/article/details/80256530
steps = np.where(draws > 0,1,-1)
walks = steps.cumsum(1)
walks
array([[ -1,   0,  -1, ..., -36, -35, -36],
       [ -1,  -2,  -1, ...,  44,  45,  44],
       [ -1,   0,   1, ...,  24,  23,  22],
       ...,
       [  1,   0,   1, ...,  42,  41,  42],
       [ -1,   0,  -1, ..., -16, -17, -18],
       [ -1,   0,  -1, ..., -56, -57, -58]], dtype=int32)

• 这样我们可以计算出这些随机步的最大值和最小值了：

walks.max()
118

walks.min()
-117

• 让我们在这些随机步中计算出30或-30的最小穿越时间。这有点棘手，因为不是所有的5000个都达到了30。我们可以用any方法来检查：

hists30 = (np.abs(walks) >= 30).any(1)
hists30
#array([ True,  True,  True, ...,  True, False,  True])
hists30.sum() # 达到30或-30的数字
#3396

• 我们可以使用布尔值数组来选出绝对步数超过30步所在的行，并使用argmax从轴向1上获取穿越时间：

crossing_times = (np.abs(walks[hists30]) >= 30).argmax(1)
crossing_times
# array([637, 957, 711, ..., 311, 333, 375], dtype=int32)

• 利用其他分布而不是等概率的掷硬币实验来随机漫步也是很容易的。你只需要使用一个不同的随机数生成函数，比如normal,再根据特定的均值和标准差即可生成正态分布下的随机步：

steps = np.random.normal(loc=0,scale=0.25,size=(nwalks,nsteps))