文章目录
一、Numpy数据类型与常用数组
1.1 构建ndarray
import numpy as np
维度看最外层方括号数量，一个方括号是一维，两个方括号是二维…
如果类型不匹配，NumPy 将会向上转换（字符串>浮点数>整数）
1.2 指定类型创建
1.3 查看类型ndarray.dtype
ndarray.dtype用来显示当前ndarray对象的数据属于什么类型：
1.4 类型转换ndarray.astype()
- 第一种方式： ndarray.astype(“数据类型名”)
- 第二种方式： ndarray.astype(np.数据类型名)
1.5 常用的数组
1.5.1 np.arange()
和普通数组创建语法一样
1.5.2 np.linspace()
np.linspace(start, stop, num=50, endpoint=True)
- 在指定的间隔内返回均匀间隔的数字，用作相同间隔采样。
- start：标量,序列的起始值。
- stop：标量,除非"endpoint"设置为False，否则为序列的结束值。
- num：int，可选。要生成的样本数。默认值为50.必须为非负数。
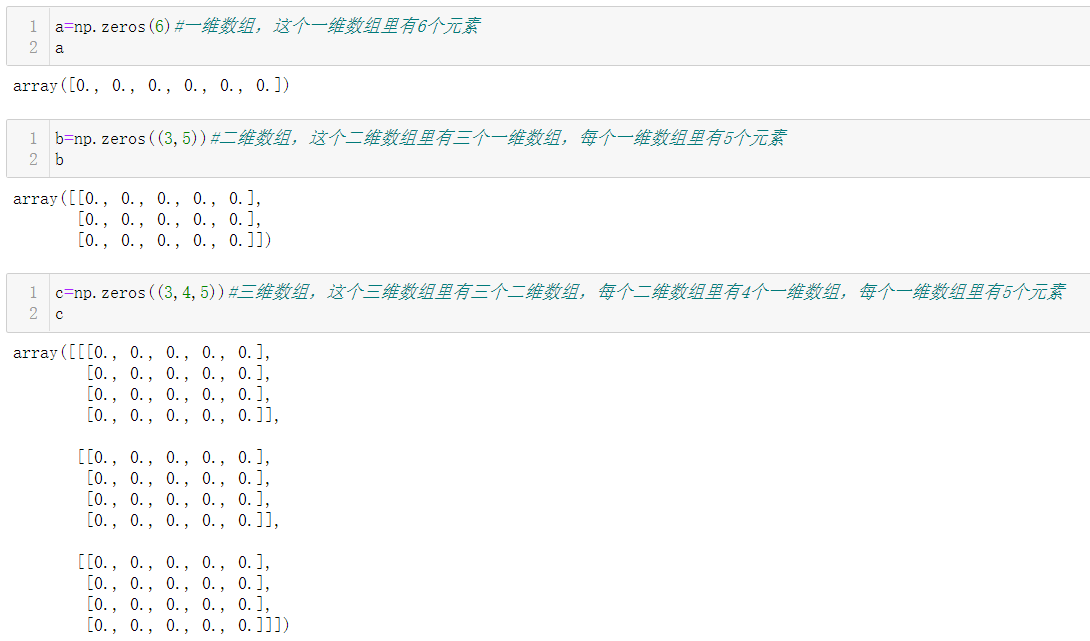
1.5.3 np.zeros()
1.5.4 np.ones()
1.5.5 np.eye()
返回一个二维数组，其中对角线为1，零点为零的二维数组。（单位矩阵）
1.5.6 np.full()
返回给定形状和类型的新数组，填充fill_value
- np.full（shape，fill_value，dtype = None）
- shape：int或int的序列新数组的形状，例如（2,3）或2。
- fill_value：标量填充值。
- dtype：数据类型，可选数组所需的数据类型默认值为"None"。
1.5.7 设置空值
np中缺失值用np.nan表示，其他ndarry对象与之运算的结果都为缺失值，运算结果数组的形状与参与运算的数组的形状 一致。
1.5.8 随机数组
1.5.8.1 np.random.randint()
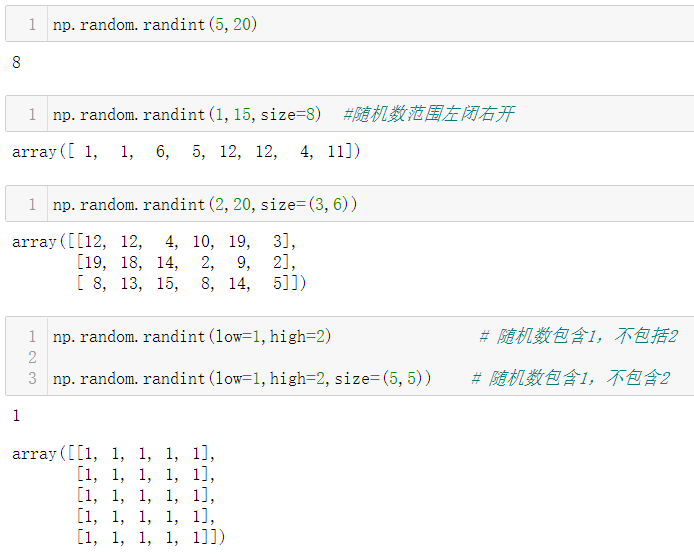
1.5.8.2 np.random.random()
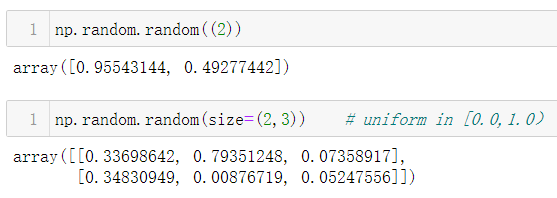
1.5.8.3 np.random.uniform()
- 语法：np.random.uniform(low=0.0, high=1.0, size=None)
- 返回随机浮点数，在半开区间[a,b)中。
1.5.8.4 np.random.randn()
- 语法：np.random.randn(形状)
- 从“标准正态”分布中返回一个样本（或样本）。
1.5.8.5 np.random.normal()
- 语法：normal（平均值，标准偏差，形状）
- 作用：从正态分布中抽取随机样本。
- 如果平均值和标准差为0和1，或者不写这两个参数，就等同于
- np.random.randn()
1.5.8.6 np.random.choice()
1.5.8.7 np.random.shuffle()
通过混洗其内容来就地修改序列。此功能仅沿a的第一轴洗牌。
-
np.random.shuffle(x)
- x：array_like（要洗牌的数组或列表）。
-
对于一维数组，打乱的对象是一个个元素的顺序
-
对于二维数组，打乱的对象是一个个一维数组
-
对于三维数组，打乱的对象是一个个二维数组
二、Numpy属性、索引和切片
2.1 ndarray常用属性
2.1.1 np.random.seed()
若不设定随机数种子，那么每次运行后产生的随机数都不一样，设定了后产生的随机数不会自动改变
2.1.2 ndarray.shape
查看数组的形状
2.1.3 ndarray.ndim
查看数组的维度
2.1.4 ndarray.size
查看数组元素个数
2.2 数组的索引和切片
单元素索引和切片操作和普通数组一样
2.2.1 多维数组索引
注意：行和列的索引位置用逗号隔开
也可以按照以往嵌套列表元素的方法，一层一层取。但是推荐用上面那种方法
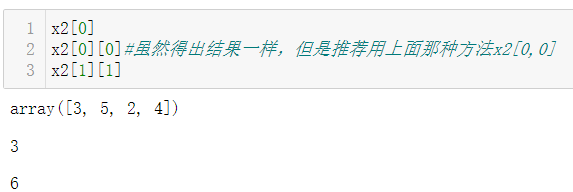例如想取红框内元素
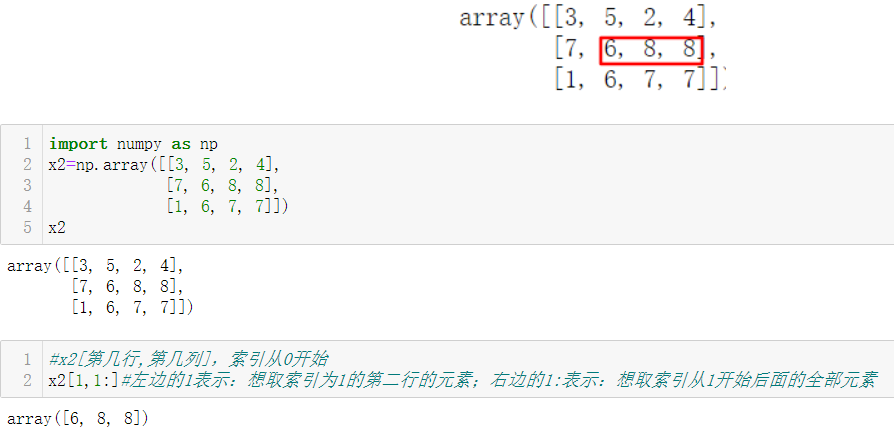
2.2.2 修改数组元素值
2.2.3 二维切片
切片语法没有任何变化
x[start:stop:step]
注意，二维数组切片的取法，下面两种方法的差异：
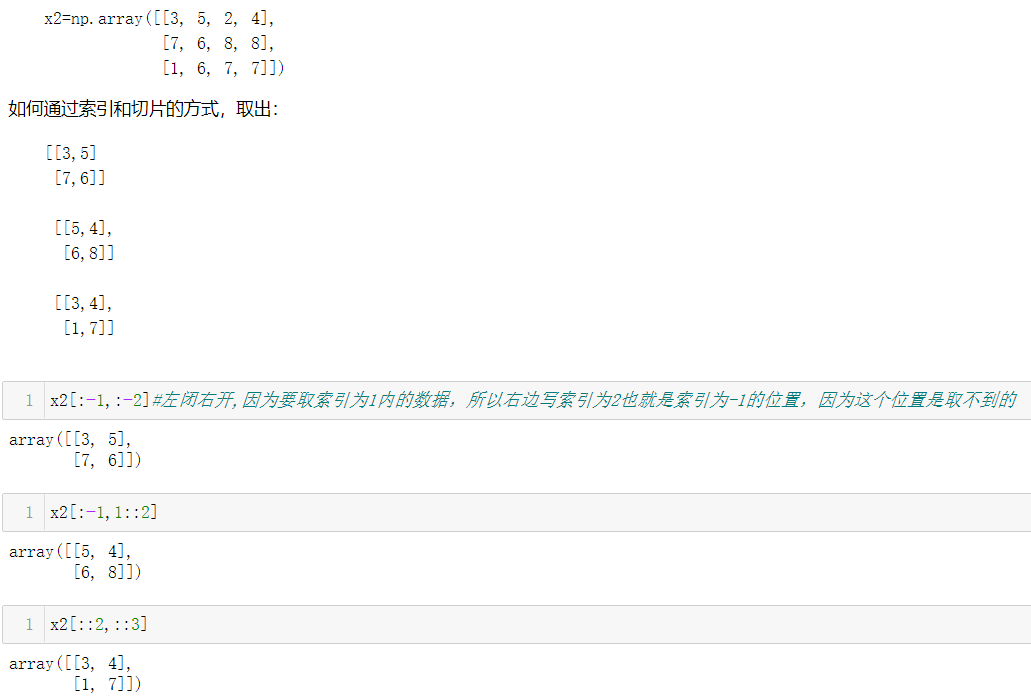
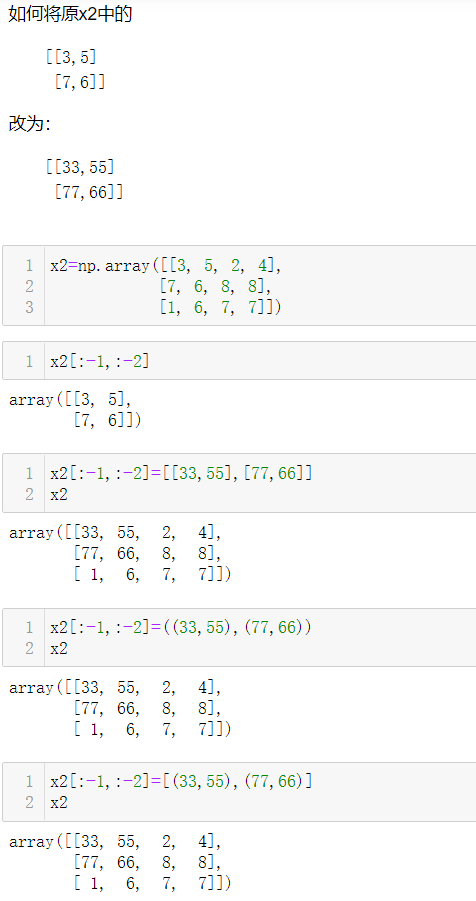
三、Numpy的变形、拼接和分裂
import numpy as np
3.1 数组的变形
3.1.1 ndarray.reshape
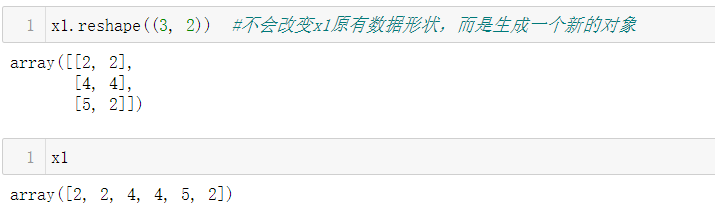
同样地，可以对3维数组进行变形，此时注意数组中元素的总和即可：
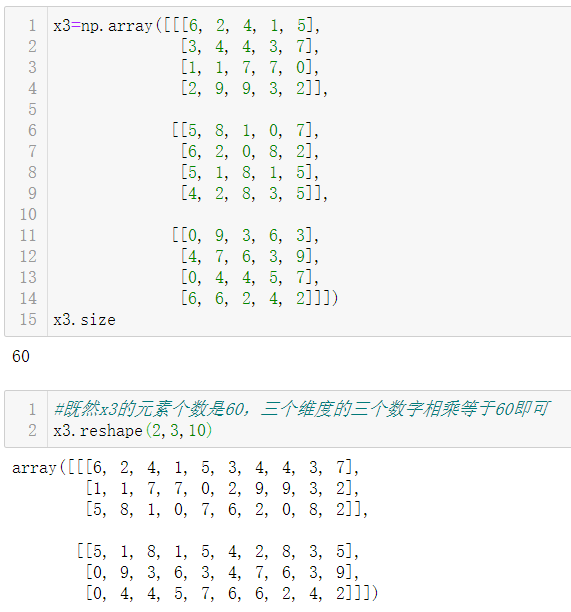
技巧：在使用 reshape 时，可以将其中的一个维度指定为 -1，Numpy 会自动计算出它的真实值
注意：只能出现一个-1
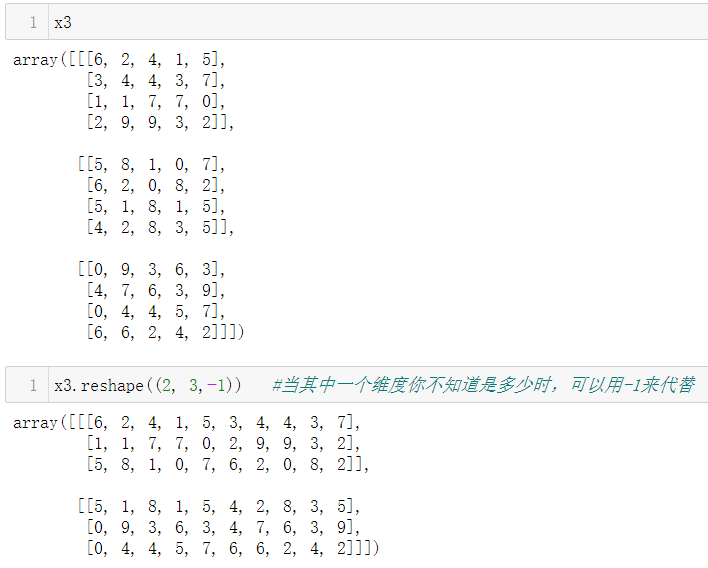
3.1.2 ndarray.shape
使用ndarray.shape有两种场景：
第一种是查看数组形状：
第二种是改变数组形状
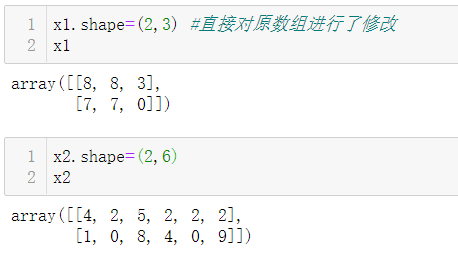
3.1.3 ndarray.resize()
使用 resize 方法可以直接修改数组本身
作用和shape改变数组形状是一样的，即改变数组本身。
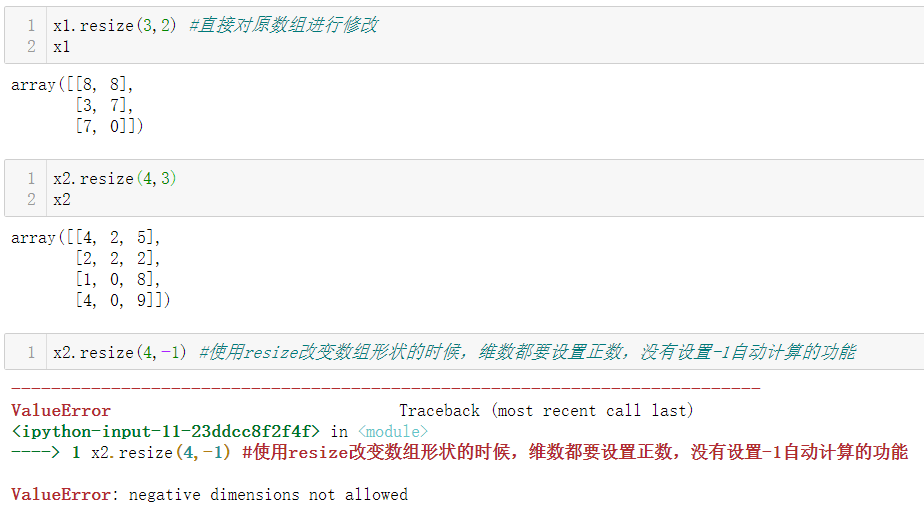
3.1.4 ndarray.ravel()
数组的平铺。
不管多少维，全部铺开变成一维。
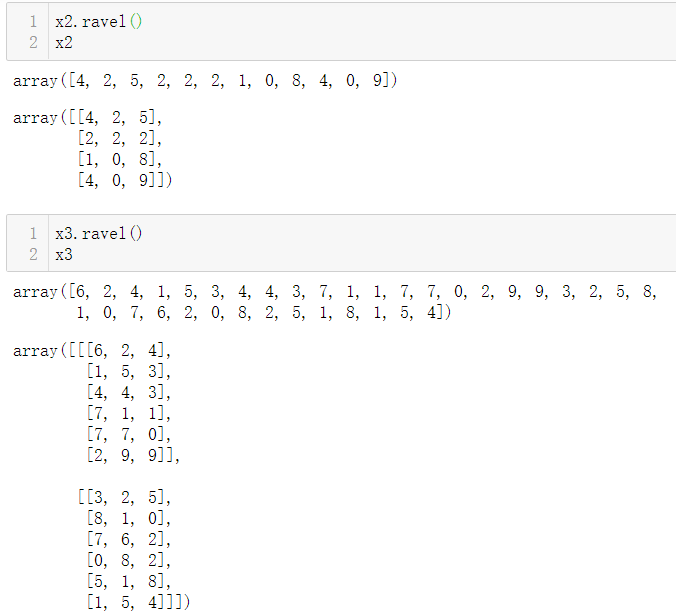
3.1.5 ndarray.T
注：无论是ravel、reshape、T，它们都不会更改原有的数组形状，都是返回一个新的数组
3.2 数组的拼接
- 一维数组只有一个轴
- axis=0 基本操作单位是一维数组里的一个个元素
- 二维数组有两个轴
- axis=0 基本操作单位是二维数组里的一个个一维数组
- axis=1 基本操作单位是一维数组里的一个个元素
- 三维数组有三个轴
- axis=0 基本操作单位是三维数组里的一个个二维数组
- axis=1 基本操作单位是二维数组里的一个个一维数组
- axis=2 基本操作单位是一维数组里的一个个元素
3.2.1 np.concatenate()
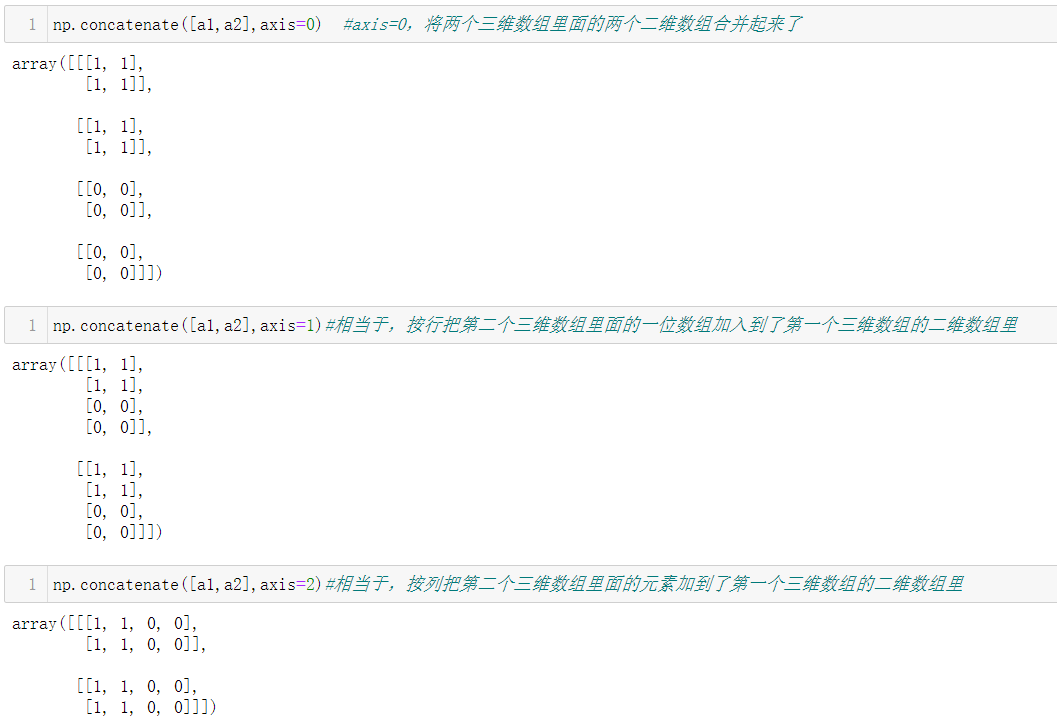
同样地,我们观察一下三维数组合并规律:
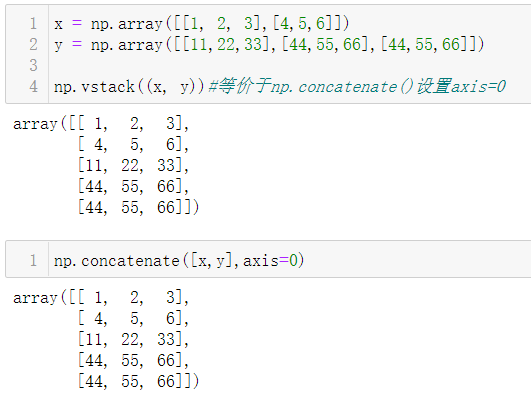
3.2.2 np.vstack()
垂直堆叠数组
3.2.3 np.hstack()
水平堆叠数组
3.3 数组的分裂
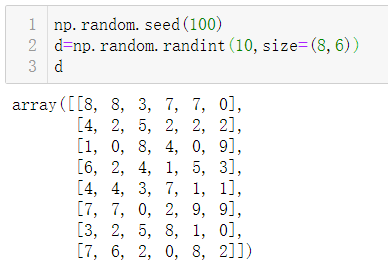
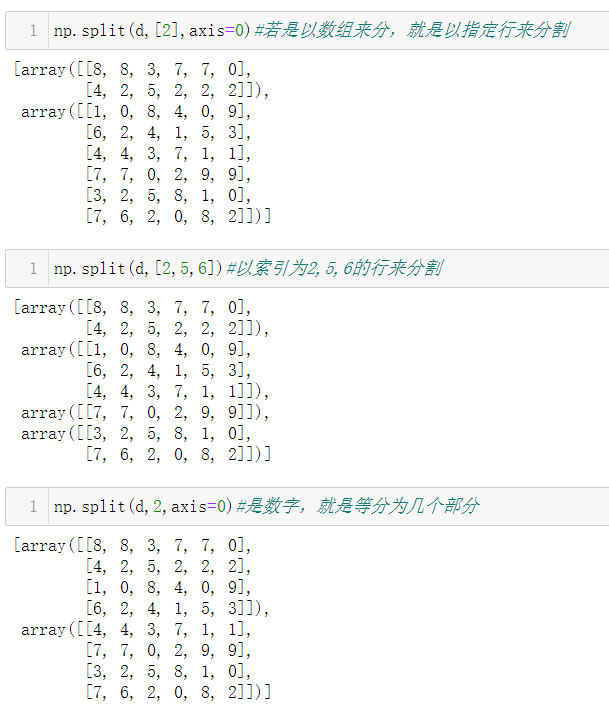
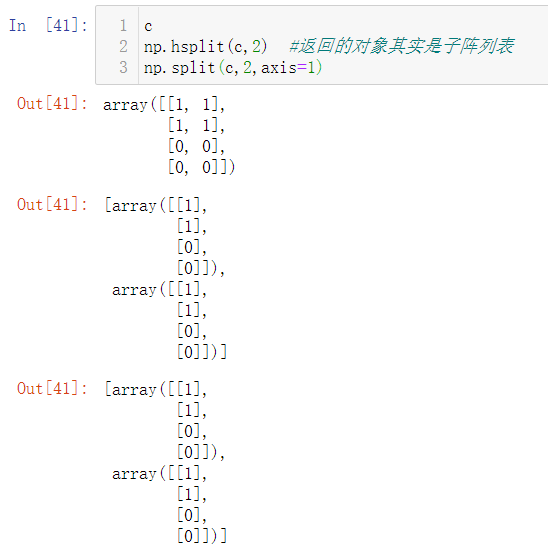
3.3.1 np.split()
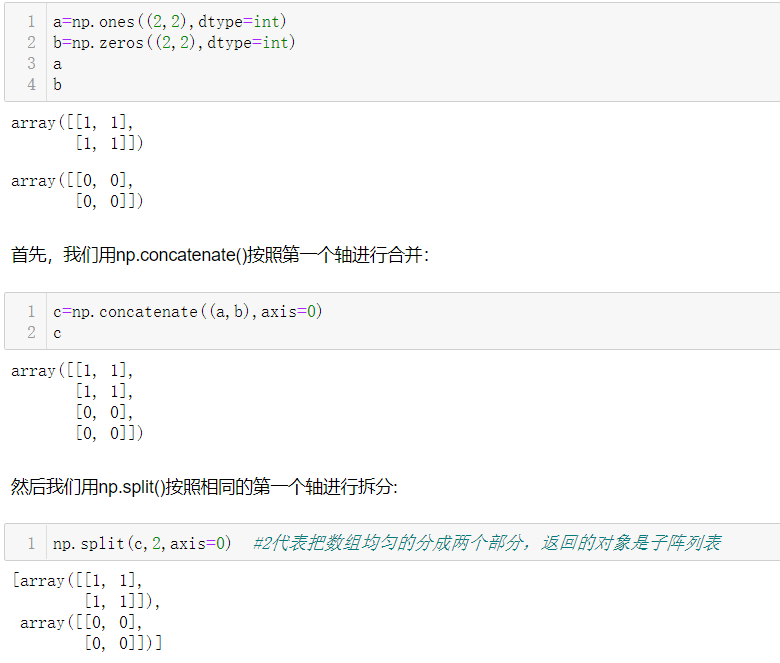因为返回的对象是子阵列表，因此是可以进行索引操作的：
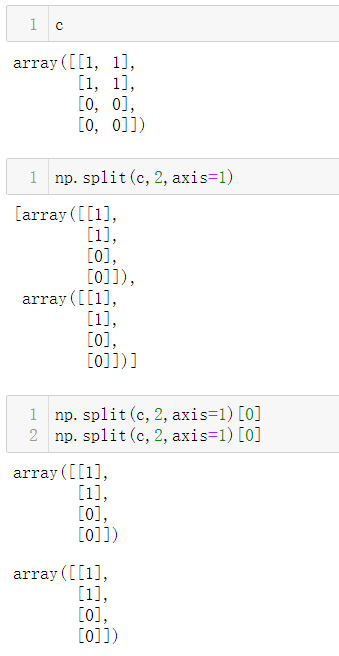
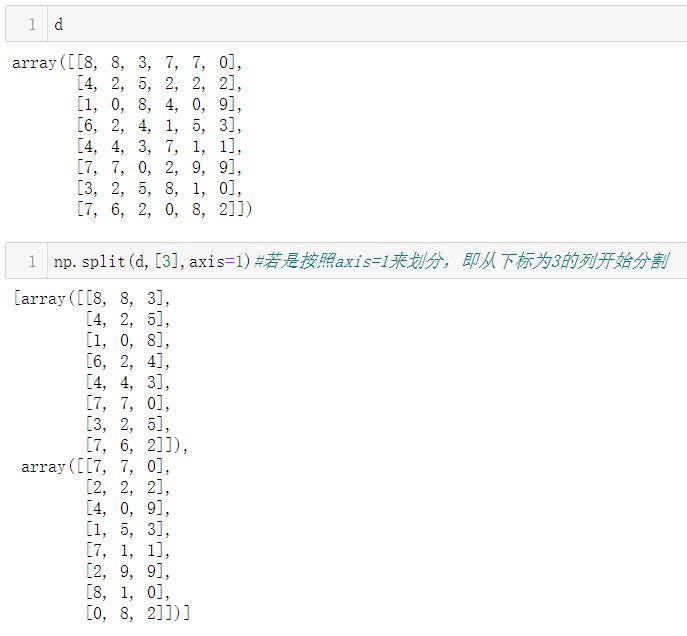
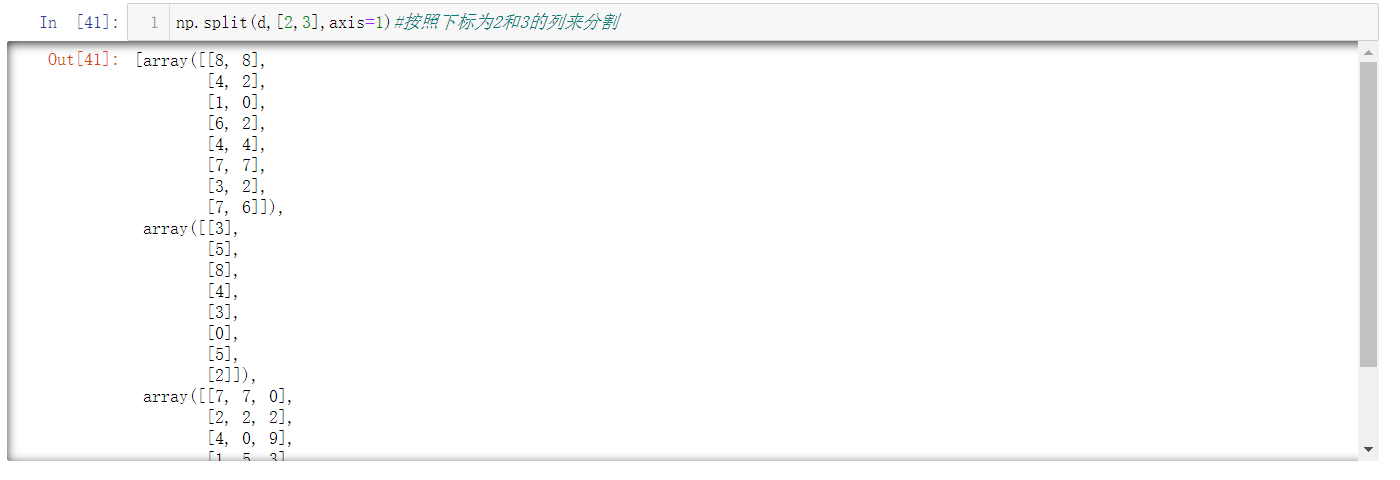
按照axis=1来划分
3.3.2 np.vsplit()
‘vsplit’相当于’split’用’axis = 0’来’拆分’
3.3.3 np.hsplit()
‘hsplit’相当于’split’用’axis = 1’来’拆分’
四、Numpy的运算与排序
常用运算基本操作和普通数组一样
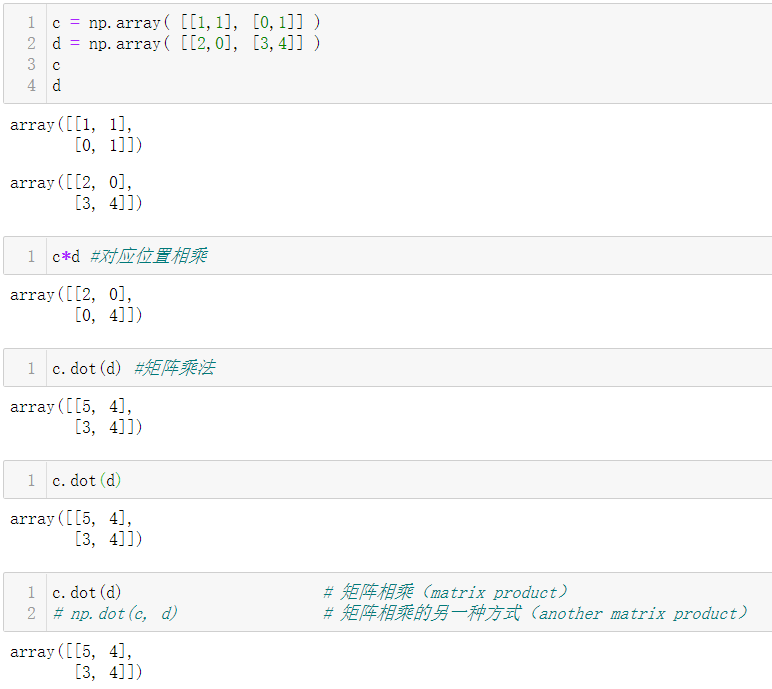
4.1 矩阵运算
- 需要注意的是，乘法运算符*的运算在NumPy数组中也是元素级别的。
- 如果想要执行矩阵乘积，可以使用dot函数：
- dot(a, b, out=None)
- 如果’a’和’b’都是1-D数组，它就是向量的内积。
- 如果’a’和’b’都是二维数组，那就是矩阵乘法。
- 如果’a’或’b’是0-D（标量），它相当于’numpy.multiply（a，b）'或’a * b’是首选。
- 如果’a’是N-D数组而’b’是1-D数组，则它是和的乘积’a’和’b’的最后一个轴。
如果a和b都是一位数组，就是求向量的内积
如果c和d都是二维数组，就是求矩阵乘法
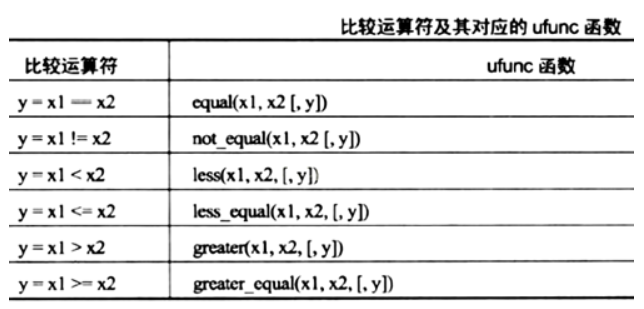
4.2 判断符的妙用
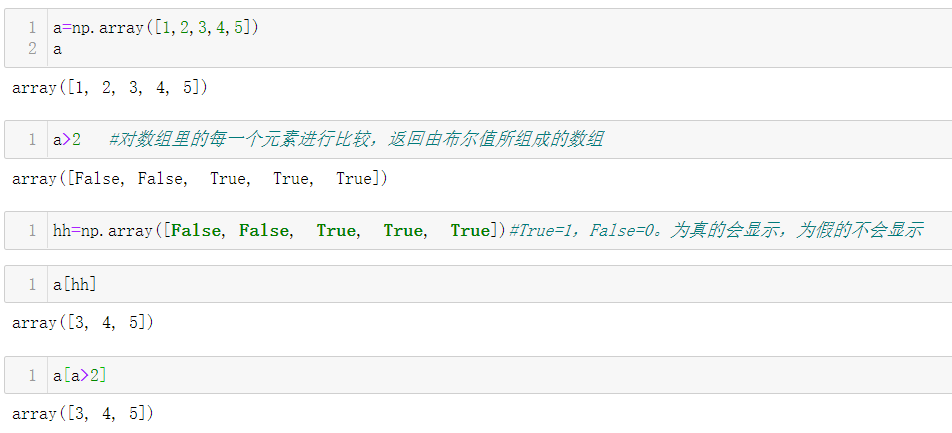
如果想要将数组a中奇数元素删除：
4.3 聚合函数
4.3.1 常用聚合函数
| 函数 | 说明 |
|---|---|
| sum | 对数组中全部或某轴向的元素。零长度的数组sum为0 |
| mean | 算数平均数。零长度的数组mean为nan |
| std、var | 标准差、方差 |
| min、max | 最大值、最小值 |
| argmin、argmax | 最大和最小元素的索引 |
| cumsum、cumprod | 累计和、累计积 |
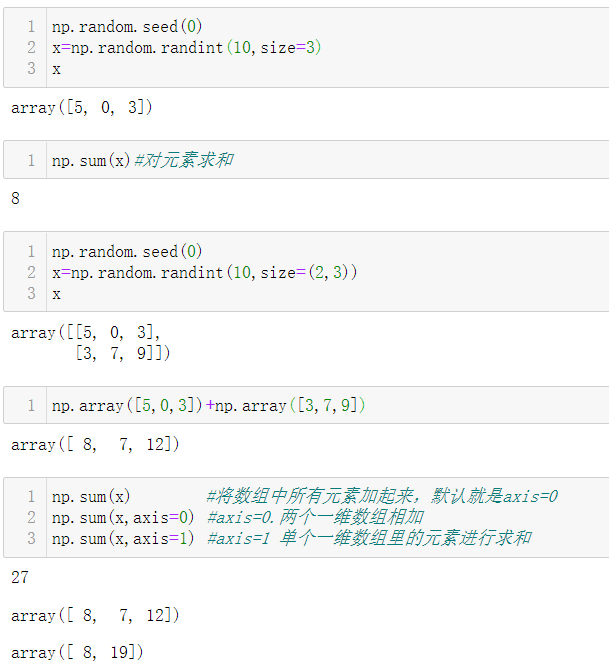上面的求和方式可以通过数组对象来调用.sum()函数：
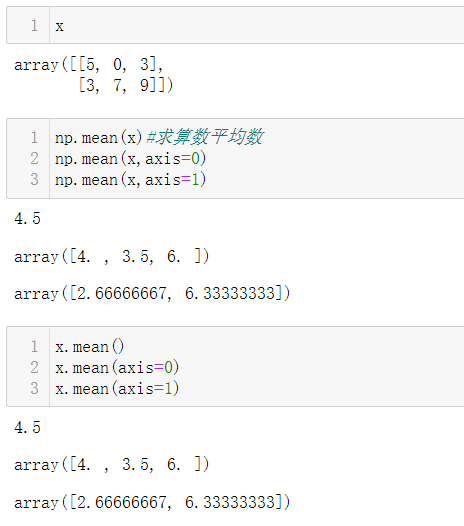
对于二维数组的操作，如果是axis=0
- 操作的对象就是一维数组之间的操作
对于二维数组的操作，如果是axis=1
- 操作的对象就是一维数组内部的一个个元素
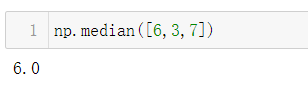
中位数
第一步：先对序列升序排列
第二步：取中间的值
如果中间的值有两个，则去中间两个值的均值
- 6、3、7由小到大排列，变成：3、6、7
- 3、6、7中间的数6就是这个序列的中位数
[6,3,7,8]
- 排序：3、6、7、8
- 取中间两个数的均值(6+7)/2=6.5
如果序列数值中，有一些过大或过小的数值，[6,3,7,8,8888]–>3,6,7,8,8888–>中位数就是7
中位数：体现序列数值的集中程度，使用中位数来描述集中程度的好处是：可以避免过大或者过小的数值的干扰
- 均值：如果用均值来描述数据的集中程度，缺点：容易受异常值干扰
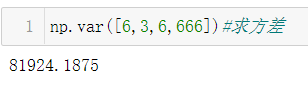
方差怎么求？
- 第一步：求出序列的均值5
- 第二步：序列中每个数值减去均值5（本意在于：求出每个数和均值之间的距离）
- 第三步：每个差值分别求平方
- 第四步：所有平方结果求和
- 第五步：求和结果除以序列中数值的数量3
标准差为方差的开方
cumsum（累计和）、cumprod（累计积）
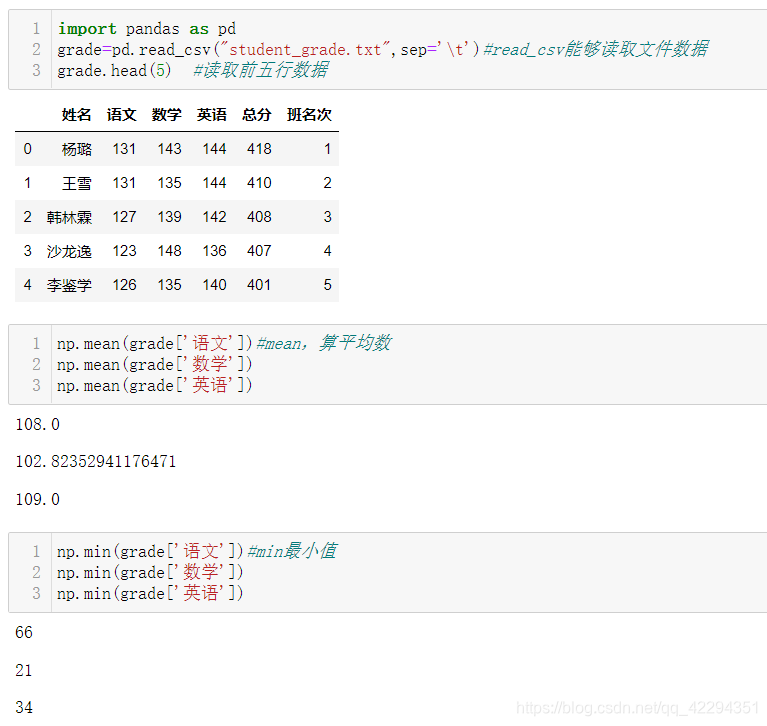
4.3.2 Numpy聚合函数使用场景
student_grade.txt文档内容如下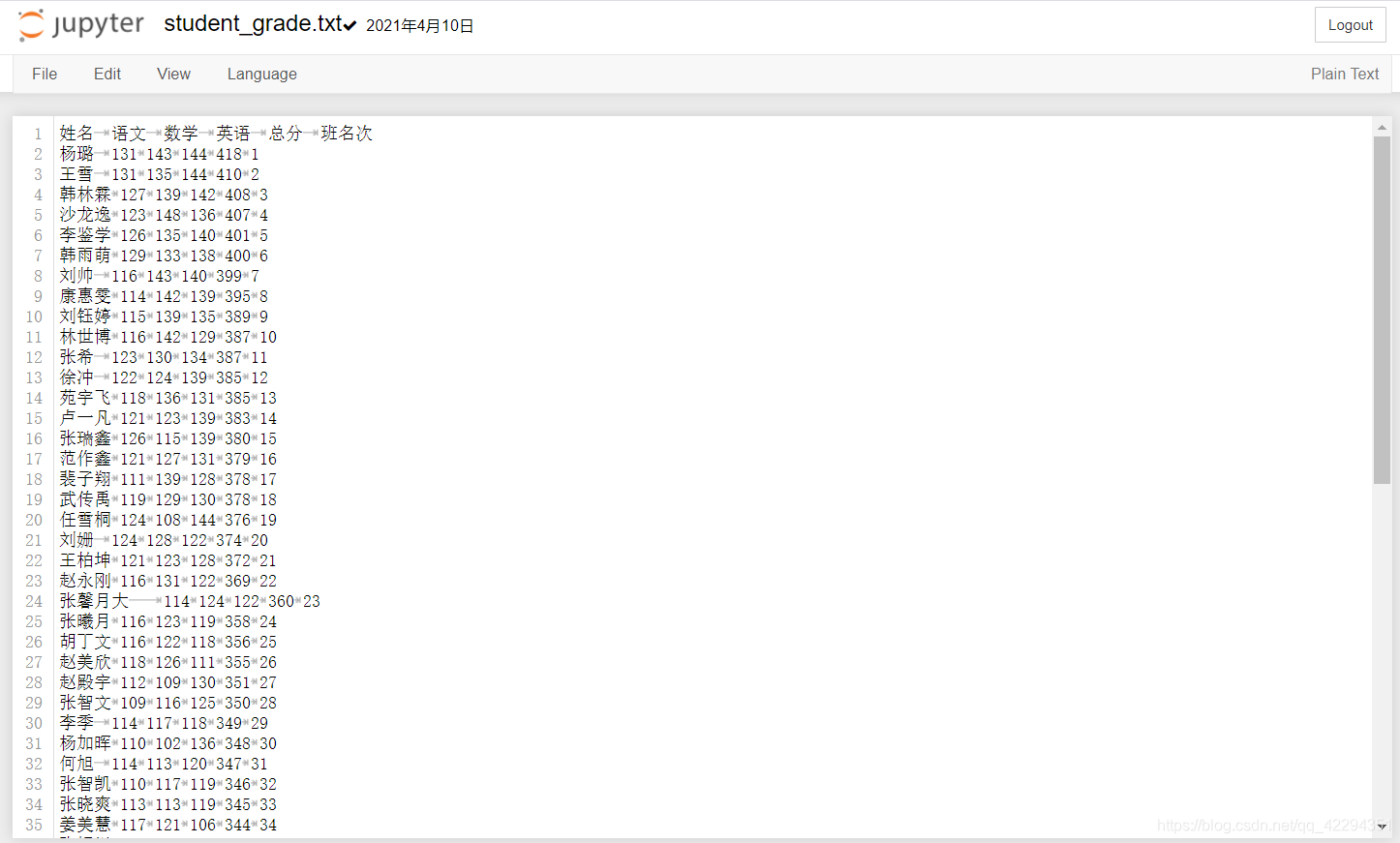
4.4 Numpy的快速排序
4.4.1 np.sort()
4.5 唯一化和集合逻辑
| 方法 | 说明 |
|---|---|
| unique(x) | 计算x中的唯一元素，并返回有序结果。 |
| intersect1d(x,y) | 计算x和y的公共元素，并返回有序结果。 |
| union1d（x,y） | 计算x和y的并集，并返回有序结果。 |
| in1d(x,y) | 得到一个表示“x的元素是否包含于y”的布尔型数组。 |
| setdiff1d(x,y) | 集合的差，即元素在x中且不在y中。 |
| setxor1d(x,y) | 集合的对称性，即存在于一个数组中但不同时存在于两个数组中的元素。 |
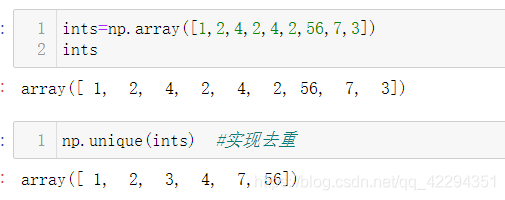
4.5.1 唯一化
np.unique()#去重
4.5.2 交集
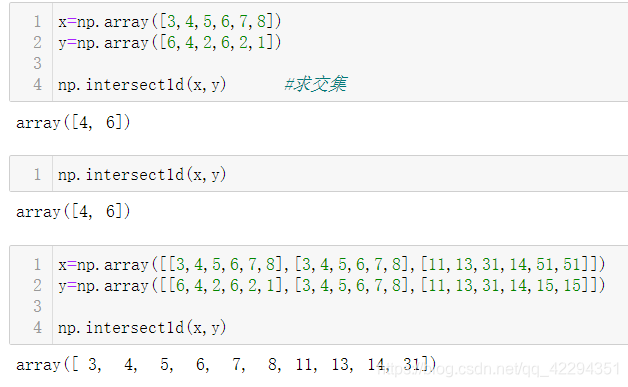
4.5.3 并集（去重）
4.5.4 差集
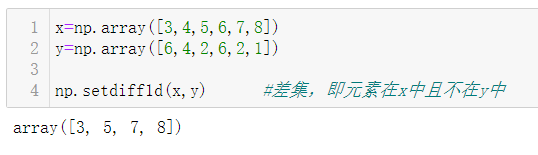
4.5.5 补集
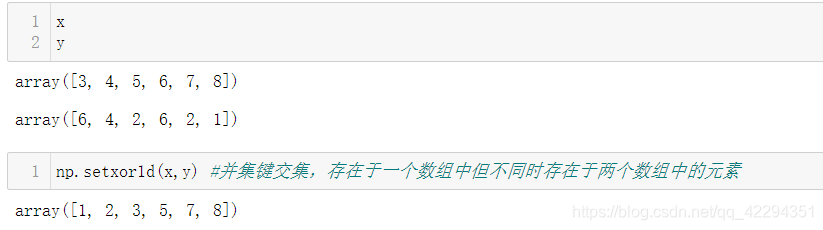
五、Numpy数组拉伸和函数向量化
5.1 数组拉伸
5.1.1 列表推导式
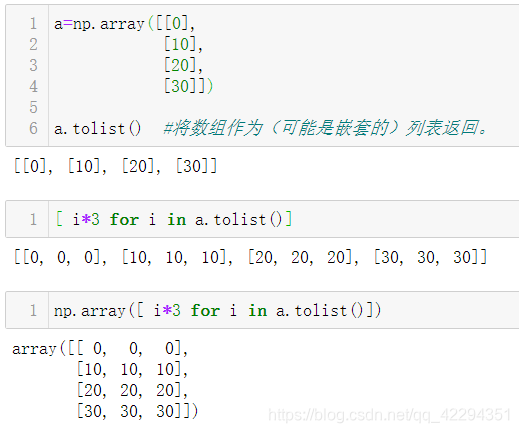
5.2 函数的向量化
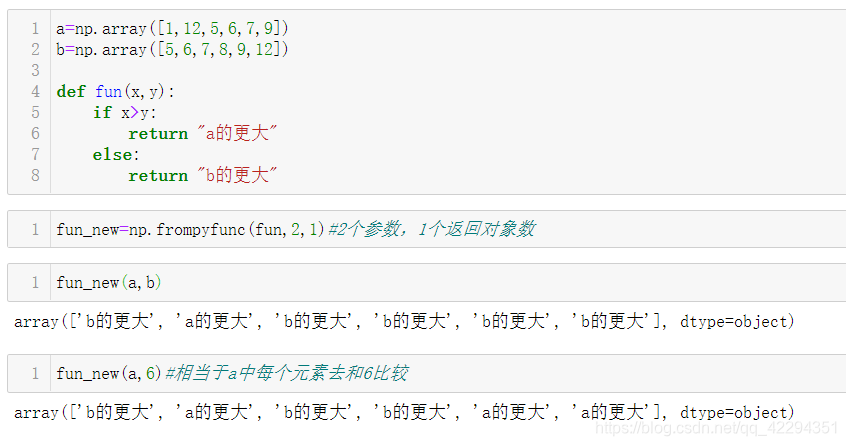
5.2.1 frompyfunc 函数
frompyfunc（func，nin，nout）
- 采用任意Python函数并返回NumPy ufunc。
- 例如，可以用于向内置Python添加广播功能。
- 参数
- func：Python函数对象，任意Python函数。
- nin：int，输入参数的数量。
- nout：int，'func’返回的对象数。（NumPy通用函数（ufunc）对象。）
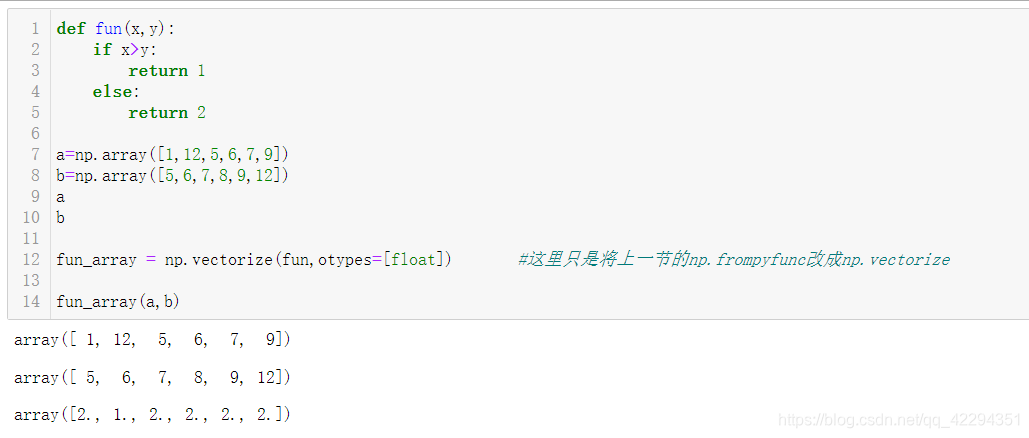
5.2.2 vectorize 函数
np.vectorize([‘pyfunc’，‘otypes = None’）
- 定义一个矢量化函数，它接受一组嵌套的对象或numpy数组作为输入并返回单个numpy数组或元组输出。
- pyfunc：可调用python函数或方法。
- otypes：str或dtypes列表，可选输出数据类型。必须将其指定为字符串typecode字符或数据类型说明符列表。应该是每个输出的一个数据类型说明符。
需要注意的是，vectorize函数主要作用是提供便利，而不是性能。它的实现本质上是for循环。
