开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> Python知识库 -> Python程序设计作业2 -> 正文阅读

[Python知识库]Python程序设计作业2

1. 完成课程讲义中状态机的实现：

在这里插入图片描述

(1) 累加器 Accumulator

例子：列表[-1, 2, 3, -2, 5, 6]中的数字相加，我们得到和是 13。
output = Accumulator().transduce([-1,2,3,-2,5,6]) #output=[-1, 1, 4, 2, 7, 13]

(2) 二进制相加 Binary_Addition

例子：011 和 001 相加我们得到 100。
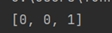
output = Binary_Addition().transduce([(1,1),(1,0),(0,0)]) #output=[0, 0, 1]

(3) 反向器 Reverser

实现一个反向器，逆向输出一个序列。输入的形式如下：
sequence1 + [‘end’] + sequence2
其中 sequence1 是字符串列表，‘end’表示 sequence1 的终结，sequence2 为任意序列。反向器的作用如下：当 sequence1 里的每个元素输入时，反向器输出 None。当[‘end’]和 sequence2 的每个元素输入时，反向器依次反向输出 sequence1 中的元素；当没有元素输出时，则输出 None。

例子：
output = Reverser().transduce([‘foo’,’ ', ‘bar’] + [‘end’] + list(range(5))) #output = [None, None, None, ‘bar’, ’ ', ‘foo’, None, None, None]
解释：输出中前三个 None 为输入 sequence1 时输出。从输入‘end’开始，sequence1 中的元素开始反向输出。sequence1 输出完毕后，继续输出 None。（即输入 list(range(5))中的 2，3，4 时）。

更多测试例子：

①output=Reverser().transduce([‘foo’, ’ ', ‘bar’] + [‘end’] + [‘end’]*3+list(range(2)))
#output = [None, None, None, ‘bar’, ’ ', ‘foo’, None, None, None]

②output = Reverser().transduce(list(‘the’) + [‘end’] + list(range(3)))
#output = [None, None, None, ‘e’, ‘h’, ‘t’, None]

③output=Reverser().transduce([] + [‘end’] + list(range(5)))
#output = [None, None, None, None, None, None]

④output=output=Reverser().transduce(list(‘nehznehS evol I’) + [‘end’]+ list(range(15)))
#output = [None, None, None, None, None, None, None, None, None, None, None, None, None, None, None, ‘I’, ’ ', ‘l’, ‘o’, ‘v’, ‘e’, ’ ', ‘S’, ‘h’, ‘e’, ‘n’, ‘z’, ‘h’, ‘e’, ‘n’, None]

实现要求：
（1）不同的状态机子类继承父类 SM；
（2）补充父类的 transduce 函数，子类不能重写 transduce 函数；
（3）补充每个子类的 transition_fn 和 output_fn 函数，其中累加器的实现代码如下：

class Accumulator(SM): 
    start_state = 0
    def transition_fn(self, s, x): 
        return s + x
    def output_fn(self, s): 
        return s

建议：利用累加器的代码实现父类的 transduce 函数，再实现二进制相加和反向器的 transition_fn 和 output_fn 函数。

【解题思路】
①定义状态机：
首先定义一个状态机，设置初始状态用于传递运行状态。然后定义初始状态转移函数与输出函数。只在父类中定义基本的方法即可，并只需实现状态转移的transduce方法即可，其他方法在子类中实现即可。

②定义累加器类：
累加器类是继承于状态机类的子类。对于累加器类，可以根据下一状态都等于上一状态加上传入的参数的特性编写状态转移函数。对于输出函数，只需直接返回累加完的当前状态表示结果即可。

③定义二进制加法类：
二进制加法类是继承于状态机类的子类。对于二进制加法类，采取一个元组表示当前状态值，元组的第一个元素表示进位值，即记录低一位是否产生进位。元组的第二个元素表示已经计算的当前结果，由于二进制是逆序存储的，故对于每次加法，只需将计算出来的结果append到列表的结尾即可。
对于每次加法，一共有4种可能情况，穷举4种情况，依次进行判断即可。
最后的输出函数，需要再对最终是否产生进位进行一次判断，如果不产生进位，则直接返回元组的第二个参数即可；如果产生进位，则先执行append(1)后，再返回元组的第二个元素即可。

④定义反相器：
反相器类是继承于状态机类的子类。对于反相器类，采取的方法是记录‘end’的位置，最后统一进行计算的方法。状态值是一个四元元组分别表示是否结束，len的位置，seq1的长度和已经输入的列表。在输出中直接处理即可。

【编程实现】

# 定义状态机
class StateMachine:
    def __init__(self):
        self.start_state = None  # default start state

    def transition_fn(self, s, x):
        pass

    def output_fn(self, s):
        pass

    def transduce(self, input_seq):
        for i in range(len(input_seq)):
            self.start_state = self.transition_fn(self, self.start_state, input_seq[i])
        print(self.output_fn(self, self.start_state))


# 定义累加器
class Accumulator(StateMachine):
    start_state = 0

    def transition_fn(self, s, x):
        return s + x

    def output_fn(self, s):
        return s


# 定义二进制相加器
class Binary_Addition(StateMachine):
    start_state = (0, [])  # (carry,digit)

    def transition_fn(self, s, x):
        temp = s[1]
        # 分情况判断进位
        if s[0] + x[0] + x[1] == 3:
            temp.append(1)
            s = (1, temp)

        elif s[0] + x[0] + x[1] == 2:
            temp.append(0)
            s = (1, temp)

        elif s[0] + x[0] + x[1] == 1:
            temp.append(1)
            s = (0, temp)

        else:
            temp.append(0)
            s = (0, temp)

        return s

    def output_fn(self, s):
        # 判断最高位进位
        if s[0] == 1:
            s[1].append(1)
        return s[1]


# 定义反相器
class Reverser(StateMachine):
    start_state = (0, 0, 0, [])  # isEnd,len(seq1),total lenth

    def transition_fn(self, s, x):
        # 不断刷新state中的值
        temp = s[3]
        temp.append(x)
        if s[0] == 1:
            return 1, s[1], s[2] + 1, temp
        if x == 'end':
            return 1, s[1], s[2] + 1, temp
        else:
            return 0, s[1] + 1, s[2] + 1, temp

    def output_fn(self, s):
        # 循环获取输出
        res = []
        for i in range(s[2]):
            if i < s[1]:
                res.append(None)
            elif s[1] <= i <= 2 * s[1] - 1:
                res.append(s[3][2 * s[1] - 1 - i])
            else:
                res.append(None)

        return res

首先定义状态机父类，定义构造函数，输出函数，状态转换函数，以及transduce函数。通过仔细观察几个输入样例，不难发现，输入的list中的项数跟需要操作的次数相同，因此可以直接使用循环循环插传入list的长度，然后调用输出函数即可。
累加器类是继承于状态机类的子类。对于累加器类，可以根据下一状态都等于上一状态加上传入的参数的特性编写状态转移函数。对于输出函数，只需直接返回累加完的当前状态表示结果即可。
二进制加法类是继承于状态机类的子类。对于二进制加法类，采取一个元组表示当前状态值，元组的第一个元素表示进位值，即记录低一位是否产生进位。元组的第二个元素表示已经计算的当前结果，由于二进制是逆序存储的，故对于每次加法，只需将计算出来的结果append到列表的结尾即可。对于每次加法，一共有4种可能情况，即产生进位与否，当前位是0还是1。依次进行判断即可。最后的输出函数，需要再对最终是否产生进位进行一次判断，如果不产生进位，则直接返回元组的第二个参数即可；如果产生进位，则先执行append(1)后，再返回元组的第二个元素即可。
反相器类是继承于状态机类的子类。对于反相器类，采取的方法是记录‘end’的位置，最后统一进行计算的方法。状态值是一个四元元组分别表示是否结束，len的位置，seq1的长度和已经输入的列表。在输出中直接处理即可。最后输出时，只需首先输出seq1的长度个None，然后依次进行反向输出，最后再补齐None即可。

【测试结果】
（1）累加器：
输入：
在这里插入图片描述

输出：
在这里插入图片描述
（2）二进制加法器：
输入：

输出：
在这里插入图片描述

（3）反相器：
①
输入：
在这里插入图片描述

输出：
在这里插入图片描述

②
输入：
在这里插入图片描述
输出：

③
输入：
在这里插入图片描述

输出：
在这里插入图片描述

④
输入：
在这里插入图片描述

输出：
在这里插入图片描述

[None, None, None, None, None, None, None, None, None, None, None, None, None, None, None, ‘I’, ’ ', ‘l’, ‘o’, ‘v’, ‘e’, ’ ', ‘S’, ‘h’, ‘e’, ‘n’, ‘z’, ‘h’, ‘e’, ‘n’, None]

2. 纸牌游戏：

本次作业我们将设计和实现一个扑克牌游戏。游戏规则如下：

游戏开始时，扑克牌在两名玩家中平分（扑克牌总共 52 张，每位玩家分 26张）。
在每个回合中，两个玩家都会展示手中的第一张牌。扑克牌等级较高的玩家将同时获得这两张牌，并添加到自己的牌组中。然后玩家们重新调整手牌。
若（2）中两位玩家的扑克牌等级一样（即打平），玩家们将展示手中的第二张牌。如果不再有平局，扑克牌等级较高的玩家将同时获得这四张牌；如果继续平局，玩家们将展示手中的第三、四、……张牌，直到平局被打破。
游戏持续到一个玩家收集完所有 52 张牌为止。若（3）中平局持续到一方无牌，则还有手牌的玩家获胜；若两个玩家都没有牌了，则打平。

想一想，为了实现上面这个游戏，我们需要什么类和方法？我们知道每张扑克牌都有一个花色和一个等级，如红桃 K。因此，创建一个“扑克牌”（Card）的类，并包含这两个“属性”是有意义的。此外，在我们的游戏中，“大”的扑克牌是指等级较高的牌；“打平”的牌是指等级相同的牌（不管两张牌的花色）。所以我们需要自定义一些规则来衡量“大”、“小”、“相等”的牌。

每位玩家都有一“手”牌（Hand），是扑克牌的集合，我们也可以将它写成一个类，可以从一“手”牌中取出牌、或者洗牌。一“手”牌中如果包含所有的 52 张扑克牌，叫牌堆（Deck）。每位玩家（Player）有一“手”牌和名字。
最后我们需要一个类叫 Game，实现游戏的逻辑。

作业任务：
补充提供的文件 card_game.py 中 Card，Hand，Deck，Player，Game 类的实现（标注“补充代码”处）。测试代码以验证正确性。

【解题思路与补全代码】
1、补全类的比较函数：
首先观察到第28行到第34行中的比较函数全部留空，需要补充，因此，只需在此补全对类的大于小于以及等于函数进行补充即可。
在这里插入图片描述
代码补充如下：

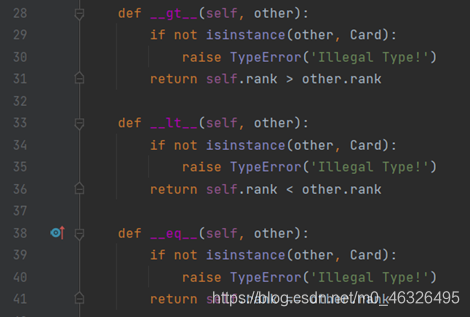
首先判断是否也为Card类，如果不为Card类，则抛出格式异常；如果也为Card类，则直接返回卡片中rank的大小即可

2、补充收到多张卡片的函数：
在这里插入图片描述
当收到多张卡片时，直接将收到的卡片列表补充在当前player的手牌列表中即可。

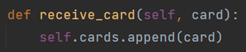
3、补充收到单张卡片的函数：

当收到一张卡片时，直接append在当前player的手牌列表中即可。
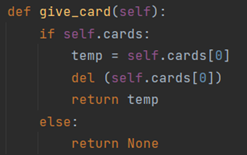
在这里插入图片描述
4、补充给出单张卡片的函数：

首先进行判空，如果为空则直接返回None，若不为空，则将第一个卡片删除，并将删除的卡片返回。

5、补充给出多张卡片的函数：

直接将该玩家的手牌全部清空，并返回即可。
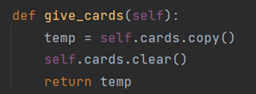
在这里插入图片描述
6、补充分配52张牌的代码：

若给牌堆分配52张一整副扑克牌，只需利用循环先遍历花色，再遍历点数并依次加入到牌堆中即可。

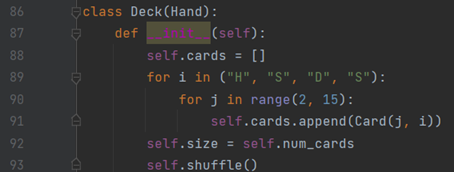
7、补充玩家类的初始化构造函数

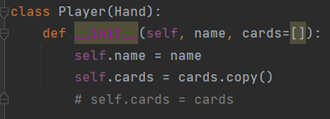
此处只需对Player的名字以及手牌进行初始化即可。要注意，此处对列表的拷贝，不能采用等号进行浅拷贝，而必须使用copy函数进行深拷贝。
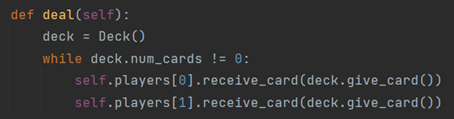
在这里插入图片描述
8、补充发牌函数：

根据注释的要求，需要实现两个人的轮流取牌，因此只需让牌堆轮流给两个人一张牌即可，直至牌堆为空。

9、补充每轮游戏代码：

首先不妨考虑两种最后的可能情况，第一种即，最后取完扑克牌后胜负已分，且牌少的输了之后正好没有牌。第二种即，一直平手，到最后一方没有牌，而输掉，因此，需要将情况分开讨论。首先对于每轮游戏，如果两个人都有牌，则可以直接一直循环游戏下去直至一方的牌为0。
为了方便进行牌的转移，不妨设置一中间变量temp
在这里插入图片描述
使用temp来完成每次牌的比较与转移。

当两方牌数量一直大于零时，可以一直进入循环，当得到胜者，先将temp中的所有牌给到胜者，并直接返回，如果未得到结果，则进行下一次的比较。
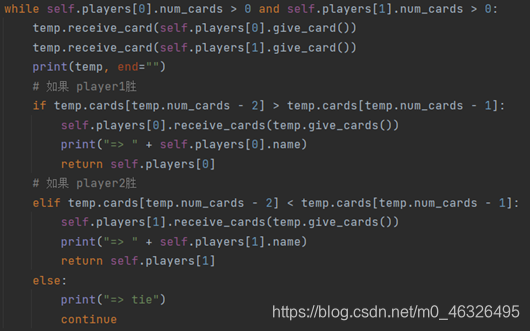
在这里插入图片描述
此外，如果在取牌过程中，尽管当前为平局，但一方的牌被取空，则被取空的一方输；若两方都同时被取空，则为平局。

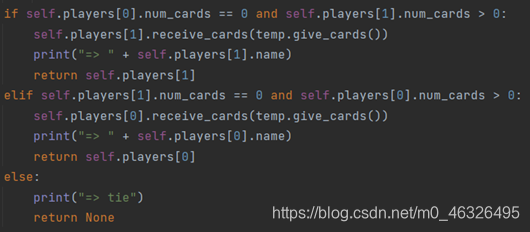
10、开始游戏的代码：
开始游戏时首先开始发牌，发牌后，则使用while循环判断两方的牌的数量并记录下最后一轮的获胜者。最终获胜者即为最后一轮的获胜者，将结果输出即可。此外，每一轮过程中由于需要重新调整两方手牌，需要对手牌进行随机排列。
在这里插入图片描述
【测试结果】
1、test_Card()

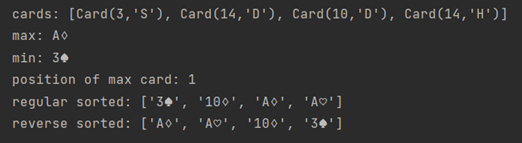
2、test_Hand()

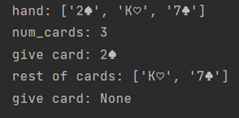
3、test_Deck()
在这里插入图片描述

4、test_Player()
在这里插入图片描述

5、test_Game()（即正式运行游戏）：
将依次输出中间过程：
非平局情况：
在这里插入图片描述
出现平局的情况：

最后结果：

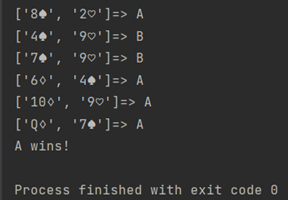
实验结论：

注意append没有返回值：在第一题的编程过程中，我使用了如下代码：

Temp = b.append(1)

本想获取列表b加了元素1后的列表，结果发现不论怎么处理，temp均为空，通过查阅资料，发现这是由于append没有返回值造成的。因此如果想获取表b加了元素1后的列表可以待完成append后再进行操作。

通过仔细观察获得状态机的通用状态转移函数：
在第一题中，需要编写一个适用于三个继承子类的状态转移函数，通过仔细观察，我发现每次处理的次数与传入数据的长度相等。因此，我通过循环完成了传入数据长度的循环，从而完成了转态转移函数的编写。
在第二题的编程过程中，我发现一个问题，不论怎么操作Player1，另一个Player2均有相同的操作，两Player的手牌列表时刻保持一致。通过上网查阅资料，我发现，这是由于我使用的a=b进行赋值产生的问题。即对于列表使用等号，表示的是一种浅拷贝，即只传地址不传值，实际上是共用了一个列表。因此若想解决这个问题，可以采用列表的copy方法，即：