[Python知识库]Python 科学计算4：SciPy 图论

1. Dijkstra

Dijkstra算法：求有向图一个顶点到另一顶点的最短路径。

from scipy.sparse.csgraph import dijkstra

例1：求1点到9点的最短路径。

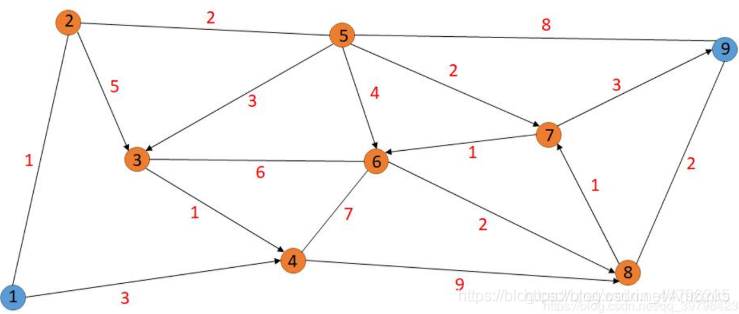
import numpy as np
from scipy.sparse.csgraph import dijkstra

inf = np.inf  # 不连通值
mtx_graph = [[0, 1, inf, 3, inf, inf, inf, inf, inf],
             [1, 0, 5, inf, 2, inf, inf, inf, inf],
             [inf, inf, 0, 1, inf, 6, inf, inf, inf],
             [inf, inf, inf, 0, inf, 7, inf, 9, inf],
             [inf, 2, 3, inf, 0, 4, 2, inf, 8],
             [inf, inf, 6, 7, inf, 0, inf, 2, inf],
             [inf, inf, inf, inf, inf, 1, 0, inf, 3],
             [inf, inf, inf, inf, inf, inf, 1, 0, 2],
             [inf, inf, inf, inf, 8, inf, 3, 2, 0]]
print(dijkstra(mtx_graph)[0][8])

输出：

8.0

2. Floyd

Floyd算法通过动态规划解决任意两点间的最短路径（多源最短路径）的问题，可以正确处理负权的最短路径问题。

import numpy as np
from scipy.sparse.csgraph import shortest_path
from scipy.sparse import csr_matrix

inf = np.inf  # 不连通值
mtx_graph = [[0, 1, inf, 3, inf, inf, inf, inf, inf],
             [1, 0, 5, inf, 2, inf, inf, inf, inf],
             [inf, inf, 0, 1, inf, 6, inf, inf, inf],
             [inf, inf, inf, 0, inf, 7, inf, 9, inf],
             [inf, 2, 3, inf, 0, 4, 2, inf, 8],
             [inf, inf, 6, 7, inf, 0, inf, 2, inf],
             [inf, inf, inf, inf, inf, 1, 0, inf, 3],
             [inf, inf, inf, inf, inf, inf, 1, 0, 2],
             [inf, inf, inf, inf, 8, inf, 3, 2, 0]]
graph = csr_matrix(mtx_graph)
print(shortest_path(csgraph=graph, method="FW")[0][8])

输出：

8.0