文章福利:Python学习精选书籍10本
最大似然估计(Maximum Likelihood Estimation,MLE)是一个很成熟的估计模型参数的技术手段。早在1821年,高斯就提出了这种思想,但在一个世纪后,1922年才被发表在《关于数理统计的数学基础》上,此时发表人并不是高斯,而是现代统计科学的天才、英国统计学家?罗纳德国·费雪。

如何理解最大似然估计呢?
字面意思上看:
Maximum?最大、极大,Likelihood?看起来像,Maximum Likelihood?就可以理解为:看起来最像.. 优雅的叫法就是:极大似然。
生活小案例方面看:
暑假里,还是学生的你难得清闲,打开手机

不一会儿,你阿妈叫你吃饭,推开门后发现你在打游戏,什么也没说,然后就去吃饭了。
吃完饭后一直到晚上10点,这一整天中,你阿妈随机性的一共推门10次,其中发现你有8次在打游戏,于是你阿爸回来后就告诉你阿爸,这娃整天都在打游戏,收拾他。

?在上述这个案例中,你阿妈通过观察?‘推门看到你打游戏的次数占据总推门次数’的频率,判断总结出你这一天最大可能性的是在打游戏这个结论。这个最大可能性的推理估计的过程就可以理解为?最大似然估计。
细品一下,上述这个最大似然估计的过程很符合文章 概率和统计是一回事么? 中讨论的统计范畴,其实本质上就是统计学思想,通过数据归纳后极大程度上判断出你的行为(打游戏的概率)
上述整个推理过程如何以量化的结果来看呢?
当你阿爸听后,面部逐渐严肃,逐渐闭上眼,内心在纠结,揍还是不揍。最后还是忍了忍,文化人嘛,凡是要讲证据,决定要亲自算一算阿妈说的这件事(8次在打游戏)的最大似然估计。

?基本的一些假设:
- 那一天所干的事情分为两种,打游戏(0)和其他(1);
- 那一天所做的事中,打游戏的概率p,干其他事情的概率为1-p;
- 阿妈是随机推门的。
基于以上假设,整个事件可看做相互独立且服从同一分布:二项分布
二项分布概率函数
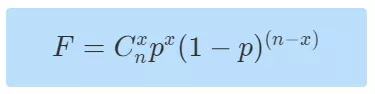
?此时请注意此概率函数与似然函数是一个模板公式,似然函数与概率函数的模型是一样的,区别只在于将谁看作变量,将谁看作参数。
概率函数:p 已知,我们可以很轻易地计算出任一事件(8次打游戏,2次其他)发生的概率。因为概率p是已知的,所以有时候为了清楚的描述一个模型,上述二项分布模型会写成下面这个形式:
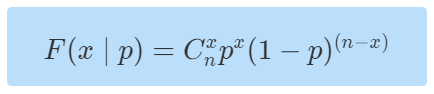
?意思是?F?在已知参数?p?的情况下,变量为?x?的模型,(x|p)左边是变量,右边是已知参数。这样写可以更清楚的知道该模型中,谁是变量,谁是已知参数。
似然函数:p未知,根据已确定发生事件(8次打游戏,2次其他)数据,可以求出在已发生的这件事上概率?p?的最大、最小值。那么此模型规范的写出来应该是:
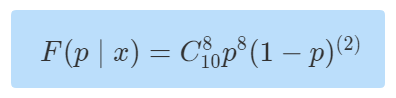
该似然函数很明显是一个关于未知概率?p?的高阶函数,也很容易的知道当?p=0?和?p=1?的时候,该函数图像和?p?轴有焦点,那么在区间(0,1)之上必然有关于该函数的最大值或最小值。
通过python画出该似然函数的曲线图
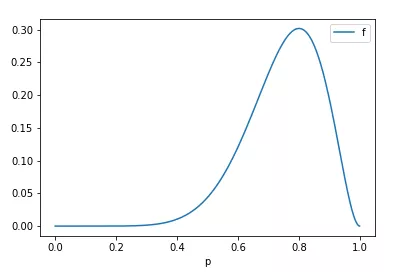
?注:【为什么求最大?满足事件(8次打游戏,2次其他)发生的概率在上图纵坐标上都有机会,但p=0和1时,概率为0,但这时事件已经发生,有理由相信概率最大(纵坐标最大值)时出现此种情况】。
然后求出最大值的取值点为?p=0.8

?也可以直接对该似然函数求导并让结果为0(求极值),在此种情况下,导函数为0的点也就是极值点了。

?上述结果?p=0.8?说明:在上述条件下的似然函数中,概率?p=0.8?时,似然函数取得最大值(发生这件事的概率最大),也就是你阿爸通过最大概率上发生这件事的数据(8次打游戏,2次其他)得出你这一天时间里有80%的时间消耗在打游戏上。
所以你阿爸已经拿着扫帚赶过来了!
--- END ---
附:二项分布极大似然函数画图源码
import pandas as pd
import numpy as np
from functools import reduce
def make_x_y(c_up=None, c_down=None):
a = reduce(lambda x, y: x * y, range(1, c_up + 1))
b = reduce(lambda x, y: x * y, range(1, c_down + 1))
c = reduce(lambda x, y: x * y, range(1, c_down - c_up + 1))
d = b / (a * c)
p = np.arange(0, 1, 0.001)
df = pd.DataFrame(p)
df.columns = ["p"]
df["p_c_up"] = df["p"].map(lambda x: x ** c_up)
df["p_c_down"] = df["p"].map(lambda x: (1 - x) ** (c_down - c_up))
df["f"] = d * df["p_c_up"] * df["p_c_down"]
return df
df = make_x_y(c_up=8, c_down=10)
chart = df.plot(x="p", y="f")
# 保存图片
fig = chart.get_figure()
fig.savefig("图片.png")更多精彩内容请关注 公众号:数据与编程之美
首发地址:极大似然估计原来很简单