前言
本篇为《使用Python进行数据分析》中介绍如何使用Matplotlib库进行数据可视化的第二篇,主要内容为如何绘制多子图,在图上添加文字和注释,如何自定义坐标轴刻度,设置自己的绘图风格,画三维图以及介绍Seaborn库的部分内容。
目录
1.绘制多子图
1.1 plt.axes
首先介绍基本的方法plt.axes,这是一种手动创建子图的方法,默认配置创建一个标准的坐标轴,还设有一个可选参数,由图形坐标系统的四个值组成[bottom,left,width,height],其使用方法和MATLAB的绘图工具一致,四个值分别代表底坐标位置,左坐标位置,宽度和高度,其数值的取值范围是左下角(原点)为0,右上角为1。
现在展示如何创建一个“画中画”。我们将参数设置为[0.65,0.65,0.2,0.2],这代表坐标轴原点位于图形高度65%与宽度65%的位置,并且坐标轴的宽度与高度设置为图形的20%。结果以及实现代码如下:
x=np.linspace(0,1,100)
y1=x**2
y2=np.sqrt(x)
ax1=plt.axes()
ax1.plot(x,y1);
ax2=plt.axes([0.65,0.65,0.2,0.2])
ax2.plot(x,y2);
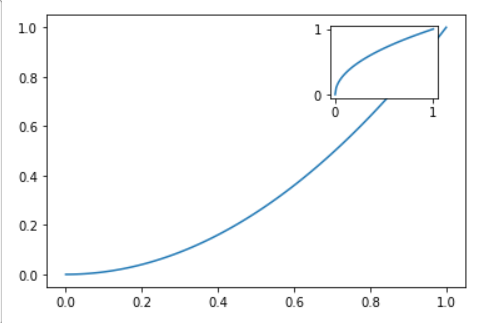
面向对象的画图接口中有类似的命令fig.add_axes()。
fig=plt.figure()
ax1=fig.add_axes([0.1,0.5,0.8,0.4],ylim=(-1.2,1.2))
ax2=fig.add_axes([0.1,0.1,0.8,0.4],ylim=(-1.2,1.2))
x=np.linspace(0,10)
ax1.plot(np.sin(x));
ax2.plot(np.cos(x));
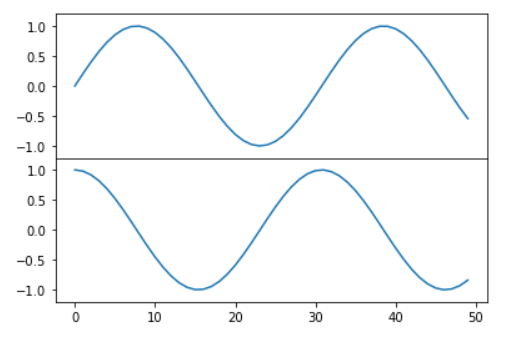
1.2 plt.subplot,plt.subplots
若干个彼此对齐的行列子图是常见的可视化任务,Matplotlib可以简便轻松地创建它们。最底层的方法是用plt.subplot()在一个网格中创建一个子图,这个命令有三个整型参数——将要创建的网格子图行数,列数和索引值,索引值从1开始,从左上角到右下角依次增大。
for i in range(1,7):
plt.subplot(2,3,i)
plt.text(0.5,0.5,str((2,3,i)),fontsize=18,ha='center')
plt.rcParams['figure.figsize']=(9.0,6.0)
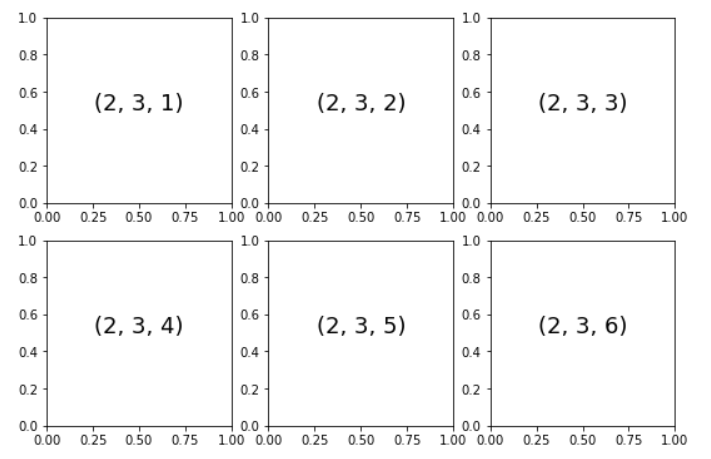
plt.subplots_adjust命令可以调整子图之间的间隔,用面向对象接口的命令fig.add_subplot()可以取得同样的效果:
fig=plt.figure()
fig.subplots_adjust(hspace=0.4,wspace=0.4)
for i in range(1,7):
plt.subplot(2,3,i)
plt.text(0.5,0.5,str((2,3,i)),fontsize=18,ha='center')
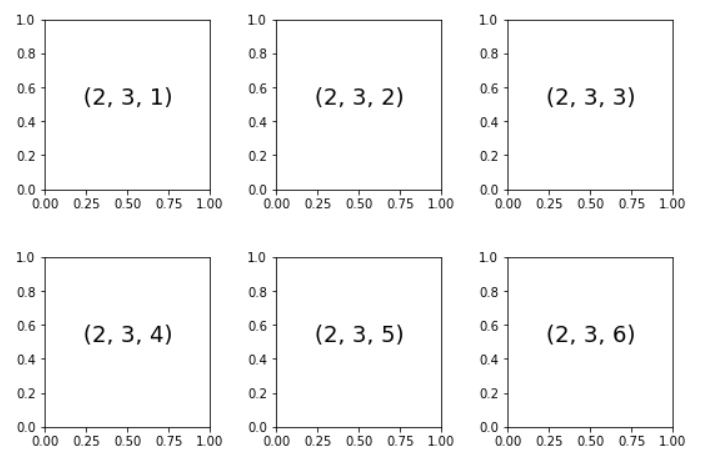
其中,hspace表示图形高度的间距,wspace表示图形宽度的间距,其取值范围为0-1,数值以子图的尺寸为单位。(如在本例中,间距是子图宽度与高度的40%)。
函数plt.subplots()可以用一行代码创建多个子图,并返回一个包含子图的NumPy数组,其关键参数是行数和列数,以及可选参数sharex与sharey(共享x轴和y轴),通过它们可以设置不同子图之间的关联关系。这在你想要创建一个大型子图或是想隐藏内部子图的x轴与y轴标题时非常好用。
fig,ax=plt.subplots(2,3,sharex='col',sharey='row')
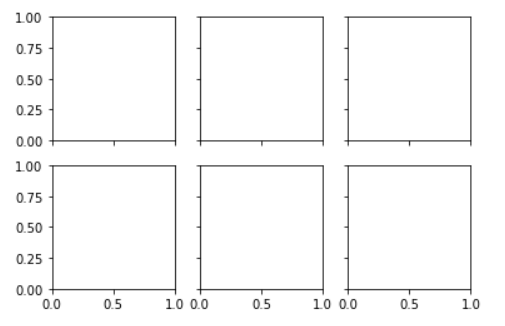
设置sharex与sharey之后,我们就可以自动去掉网格内部子图的标签,让图形看起来更整洁。坐标轴实例网格的返回结果就是一个NumPy数组,这样就可以通过标准的数组取值方式轻松获取想要的坐标轴了:
#将坐标轴存放在一个NumPy数组中,按照[row,col]取值
for i in range(2):
for j in range(3):
ax[i,j].text(0.5,0.5,str((i,j)),fontsize=18,ha='center')
fig
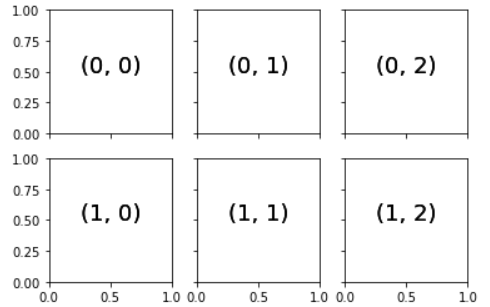
需要注意的是,与plt.subplot()相比,plt.subplots()与Python索引从0开始的习惯保持一致。(plt.subplot()与MATLAB索引从1开始类似)
1.3 plt.GridSpec
如果想实现不规则的多行多列子图网格,plt.GridSpec()是更好的工具。它本身不能直接创建一个图形,只是plt.subplot()命令可以识别的简易接口。例如,一个带行列间距的2×3网格的配置代码如下所示:
grid=plt.GridSpec(2,3)
plt.subplot(grid[0,0])
plt.subplot(grid[0,1:])
plt.subplot(grid[1,:2])
plt.subplot(grid[1,2])
plt.rcParams['figure.figsize']=(9.0,6.0)
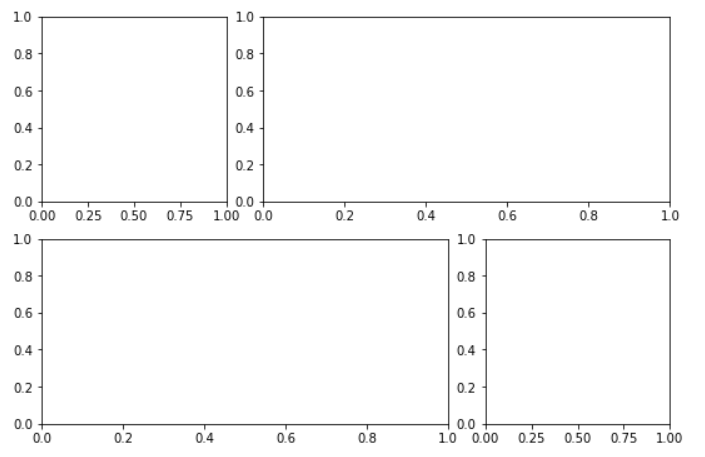
这种灵活的网格排列方式用途十分广泛,例如:
mean=[0,0]
cov=[[1,1],[1,2]]
x,y=np.random.multivariate_normal(mean,cov,3000).T
fig=plt.figure(figsize=(6,6))
grid=plt.GridSpec(4,4,hspace=0.4,wspace=0.4)
main_ax=fig.add_subplot(grid[:-1,1:])
y_hist=fig.add_subplot(grid[:-1,0],sharey=main_ax)
x_hist=fig.add_subplot(grid[-1,1:],sharex=main_ax)
main_ax.plot(x,y,'o',markersize=3,alpha=0.2)
x_hist.hist(x,40,histtype='stepfilled',orientation='vertical')
x_hist.invert_yaxis()
y_hist.hist(x,40,histtype='stepfilled',orientation='horizontal')
y_hist.invert_xaxis()
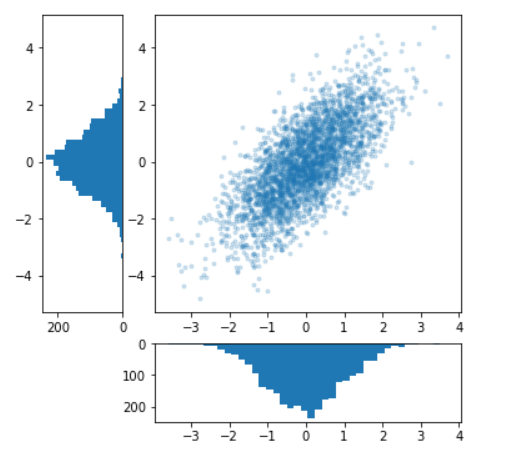
其实这种类型的图十分常见,之后我们会介绍,Seaborn库中提供了专门的API来实现这种绘图。
2.文字与注释
首先让我们在Notebook里面导入画图需要用到的一些函数:
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib as mpl
plt.style.use('seaborn-whitegrid')
import numpy as np
import pandas as pd
2.1 在图形中添加文字
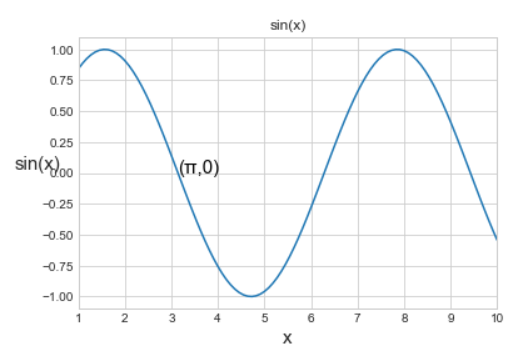
我们可以通过plt.text()/ax.text()在图形中手动添加文字注释,它们可以在具体的坐标点上放上文字。举例如下:
x=np.linspace(1,10,100)
y=np.sin(x)
plt.plot(x,y)
plt.xlim(1,10)
#添加文字标签
style=dict(size=15,color='black')
plt.text(np.pi,0,'(π,0)',ha='left',**style)
#设置坐标轴标题
plt.title('sin(x)')
plt.ylabel('sin(x)',size=15,rotation=0)
plt.xlabel('x',size=15)
2.2 坐标变换与文字位置
前面的示例将文字放在了目标数据的位置上。但有时候可能需要文字放在与数据无关的位置上,比如坐标轴或者图形中。在Matplotlib中,我们通过调整坐标变换(transform)来实现。任何图形显示框架都需要一些变换坐标系的机制。例如,当一个位于(x,y)=(1,1)位置的点需要以某种方式显示在图上特定的位置时,就需要用屏幕的像素来表示。Matplotlib提供了一类工具可以实现类似功能。
以数据为基准的坐标变换ax.transData
以坐标轴为基准的坐标变换ax.transAxes (以坐标轴维度为单位)
以图形为基准的坐标变换fig.transFigure (以图形维度为单位)
下面举一个例子,用三种变换方式将文字画在不同的位置:
fig,ax=plt.subplots(facecolor='lightgray')
ax.axis([0,10,0,10])
ax.text(1,5,'.Data:(1,5)',transform=ax.transData,size=15)
ax.text(0.5,0.1,'.Axes:(0.5,0.1)',transform=ax.transAxes,size=15)
ax.text(0.2,0.2,'.Figure:(0.2,0.2)',transform=fig.transFigure,size=15)
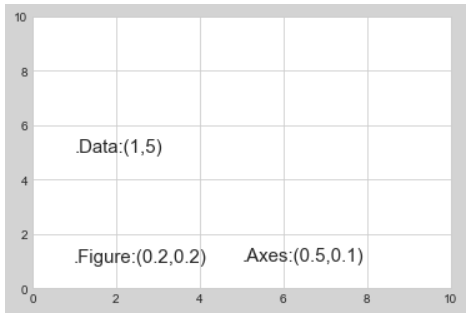
改变坐标轴的上下限只会改变transData的坐标,而其他坐标系的坐标不会发生改变,通过这样的坐标变换,就可以实现图形中坐标轴的改变了。
2.3 箭头与注释
在Matplotlib中画箭头会比想象中要困难,plt.arrow()函数与plt.annotate()函数都可以实现箭头的绘制,plt.arrow()创建出的箭头是SVG向量图对象,会随着图形分辨率的变化而改变,最终得到的结果可能并非所愿。而plt.annotate()相比之下就会灵活很多,它既可以创建文字,又可以创建箭头,并且可以对创建的对象进行灵活的配置。
演示如下:
fig,ax=plt.subplots()
x=np.linspace(0,20,1000)
ax.plot(x,np.cos(x))
ax.axis('equal')
ax.annotate('local maximum',xy=(2*np.pi,1),xytext=(10,4),arrowprops=dict(facecolor='black',shrink=0.05))
ax.annotate('localminimum',xy(5*np.pi,-1),xytext(2,-6),arrowprops=dict(arrowstyle='>',connectionstyle='angle3,angleA=0,angleB=-90')
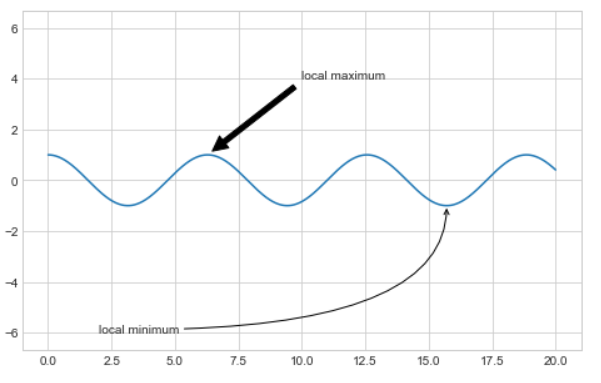
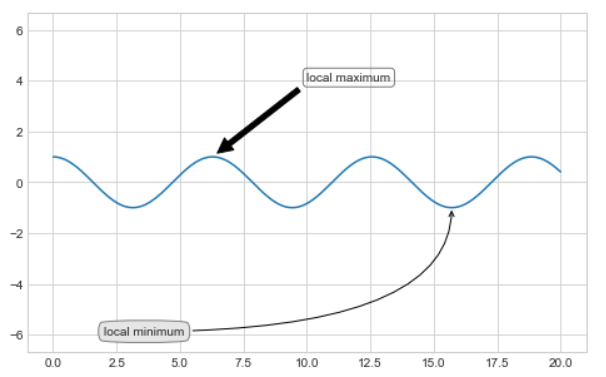
箭头的风格是通过arrowprops字典控制的,里面有许多可用的选项,在此不一一介绍,只做简单的几个演示:
ax.annotate('local maximum',xy=(2*np.pi,1),xytext=(10,4),bbox=dict(boxstyle='round',fc='none',ec='gray'),arrowprops=dict(facecolor='black',shrink=0.05))
ax.annotate('local minimum',xy=(5*np.pi,-1),xytext=(2,-6),bbox=dict(boxstyle='round4,pad=.5',fc='0.9',ec='gray'),arrowprops=dict(arrowstyle='->',connectionstyle='angle3,angleA=0,angleB=-90'))
3.自定义坐标轴刻度
3.1 格式生成器与定位器选项
| 定位器类 | 描述 |
|---|---|
| NullLocator | 无刻度 |
| FixedLocator | 刻度位置固定 |
| IndexLocator | 用索引作为定位器 |
| LinearLocator | 从min到max均匀分布刻度 |
| LogLocator | 从min到max按对数分布刻度 |
| MultipleLocator | 刻度和范围都是基数的倍数 |
| MaxNLocator | 为最大刻度找到最优位置 |
| AutoLocator | (默认)以MaxNLocator进行简单配置 |
| AutoMinorLocator | 次要刻度的定位器 |
| 格式生成器类 | 描述 |
|---|---|
| NullFormatter | 刻度上无标签 |
| IndexFormatter | 将一组标签设置为字符串 |
| FixedFormatter | 手动为刻度设置标签 |
| FuncFormatter | 用自定义函数设置标签 |
| FormatStrFormatter | 为每个刻度值设置字符串格式 |
| ScalarFormatter | (默认)为标量值设置标签 |
| LogFormatter | 对数坐标轴的默认格式生成器 |
3.2 自定义刻度格式
本节介绍常用的刻度/标签格式化操作,首先介绍最常用的隐藏刻度与标签的方法:可以通过plt.NullLocator()函数和plt.NullFormatter()函数实现,如下所示:
ax=plt.axes()
ax.plot(np.random.rand(50))
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_formatter(plt.NullFormatter())
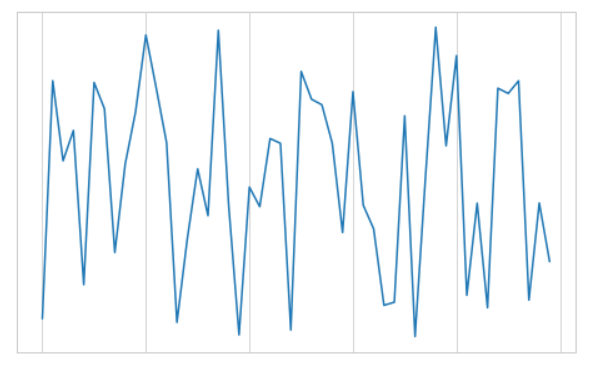
这两个函数适用于不需要刻度线和标签的场景,如上图,我们就移除了x轴的标签以及y轴的刻度线,下面我们再拿人脸的图像举例:
fig,ax=plt.subplots(5,5,figsize=(5,5))
fig.subplots_adjust(hspace=0,wspace=0)
from sklearn.datasets import fetch_olivetti_faces
faces=fetch_olivetti_faces().images
for i in range(5):
for j in range(5):
ax[i,j].xaxis.set_major_locator(plt.NullLocator())
ax[i,j].yaxis.set_major_locator(plt.NullLocator())
ax[i,j].imshow(faces[10*i+j],cmap='bone')

接下来我们介绍如何设置刻度的数量。我们可以使用plt.MaxNLocator()来解决这个问题,通过它可以设置最多需要显示多少刻度。根据设置的最多刻度数量,Matplotlib会自动为刻度安排恰当的位置。例如下图所示,刻度在显示较小的图形时会显得十分拥挤,我们可就可以通过此函数来解决这个问题:
fig,ax=plt.subplots(4,4,sharex=True,sharey=True)
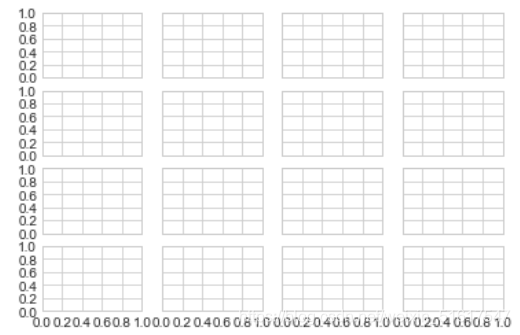
fig,ax=plt.subplots(4,4,sharex=True,sharey=True)
for axi in ax.flat:
axi.xaxis.set_major_locator(plt.MaxNLocator(3))
axi.yaxis.set_major_locator(plt.MaxNLocator(3))
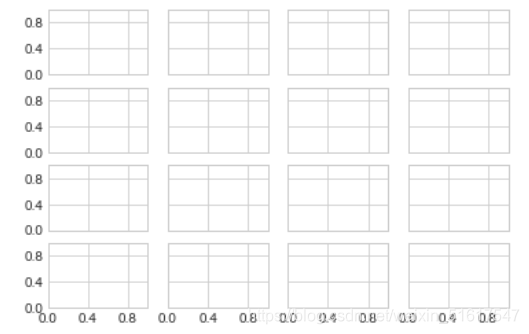
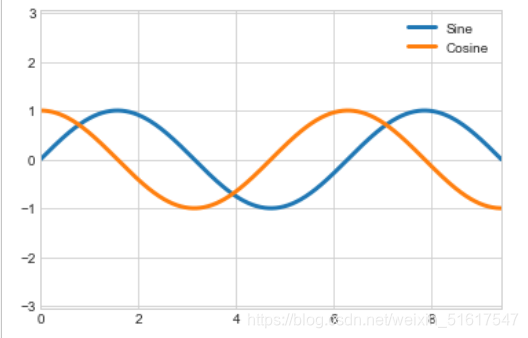
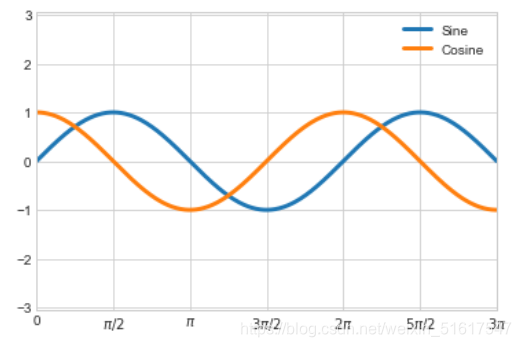
最后我们介绍如何设置花哨的刻度格式,我们不仅可以自定义主要和次要刻度的值和数量,Matplotlib还支持LaTeX的数学公式显示,只要在数学表达式两侧加上美元符号($),就可以非常方便地显示数学符号和数学公式(详情浏览文档)。示例如下:
x=np.linspace(0,3*np.pi,1000)
plt.plot(x,np.sin(x),lw=3,label='Sine')
plt.plot(x,np.cos(x),lw=3,label='Cosine')
plt.grid(True)
plt.legend(frameon=False)
plt.axis('equal')
plt.xlim(0,3*np.pi);
fig,ax=plt.subplots()
x=np.linspace(0,3*np.pi,1000)
ax.plot(x,np.sin(x),lw=3,label='Sine')
ax.plot(x,np.cos(x),lw=3,label='Cosine')
ax.grid(True)
ax.legend(frameon=False)
ax.axis('equal')
ax.set_xlim(0,3*np.pi);
ax.xaxis.set_major_locator(plt.MultipleLocator(np.pi/2))
def format_func(value,tick_number):
N=int(np.round(2*value/np.pi))
if N==0:
return '0'
elif N==1:
return r'$\pi/2$'
elif N==2:
return r'$\pi$'
elif N%2>0:
return r'${0}\pi/2$'.format(N)
else:
return r'${0}\pi$'.format(N//2)
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
4.自定义绘图风格
4.1 手动配置图形
本节我们将介绍如何修改单个图形配置,使得最终的图形比原来的图形更好看,我们可以为每个单独的图形进行个性化设置。首先,看看默认的频次直方图是什么样子的:
plt.style.use('classic')
x=np.random.randn(1000)
plt.hist(x);
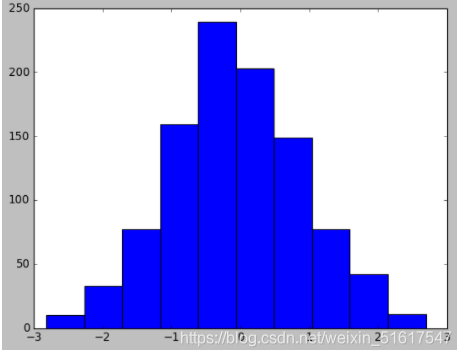
接下来,让我们通过手动调整来修改这张图像:
ax=plt.axes(facecolor='#E6E6E6')
ax.set_axisbelow(True)
plt.grid(color='w',linestyle='solid')
for spine in ax.spines.values():
spine.set_visible(False)
ax.xaxis.tick_bottom()
ax.yaxis.tick_left()
ax.tick_params(colors='gray',direction='out')
for tick in ax.get_xticklabels():
tick.set_color('gray')
for tick in ax.get_yticklabels():
tick.set_color('gray')
ax.hist(x,edgecolor='#E6E6E6',color='#EE6666')
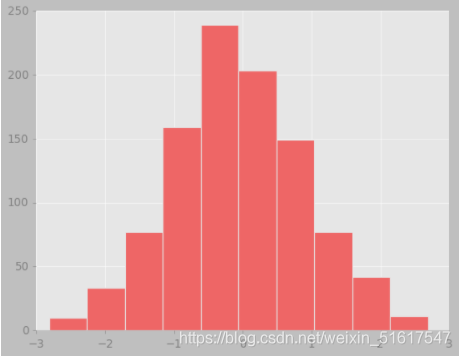
修改后的图像在外观上就比默认的设置更加美观了,下面来介绍如何可以让我们只配置一次默认图形就能将其应用到所有图形上。
4.2 修改默认配置:rcParams
Matplotlib在每次加载时,都会定义一个运行时配置(rc),其中包含了所有你创建的图形元素的默认风格。我们可以用plt.rc简便方法随时修改这个配置。现在让我们来用默认图形实现之前手动调整的效果。
首先复制一下默认的rcParams字典,这样可以在修改之后再还原回来:
IPython_default=plt.rcParams.copy()
接下来我们使用plt.rc函数来修改配置参数:
from matplotlib import cycler
colors=cycler('color',['#EE6666','#3388BB','#9988DD','#EECC55','#88BB44','#FFBBBB'])
plt.rc('axes',facecolor='#E6E6E6',edgecolor='none',axisbelow=True,grid=True,prop_cycle=colors)
plt.rc('grid',color='w',linestyle='solid')
plt.rc('xtick',direction='out',color='gray')
plt.rc('ytick',direction='out',color='gray')
plt.rc('patch',edgecolor='#E6E6E6')
plt.rc('lines',linewidth=2)
现在我们来创建一个图形看看效果:
x=np.random.randn(1000)
plt.hist(x);
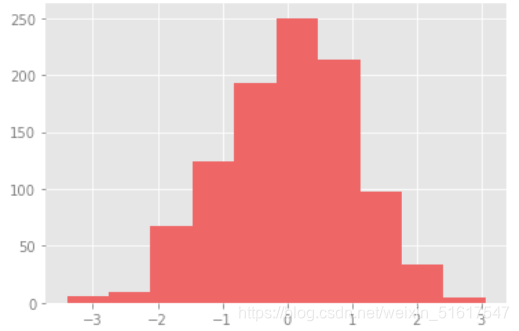
再创建一幅线图来看看rc参数的效果:
for i in range(4):
plt.plot(np.random.rand(10))
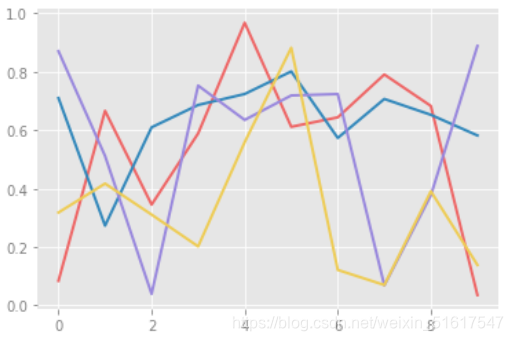
下面我们介绍几种设置好的风格(绘图风格的简要介绍可见上篇博文),首先定义一个可以绘制两种基本图形的函数:
def hist_and_lines():
np.random.seed(0)
fig,ax=plt.subplots(1,2,figsize=(11,4))
ax[0].hist(np.random.randn(1000))
for i in range(3):
ax[1].plot(np.random.rand(10))
ax[1].legend(['a','b','c'],loc='lower left')
下面我们就用这个函数来演示不同风格的显示效果。
1.默认风格
plt.rcParams.update(IPython_default)
hist_and_lines()
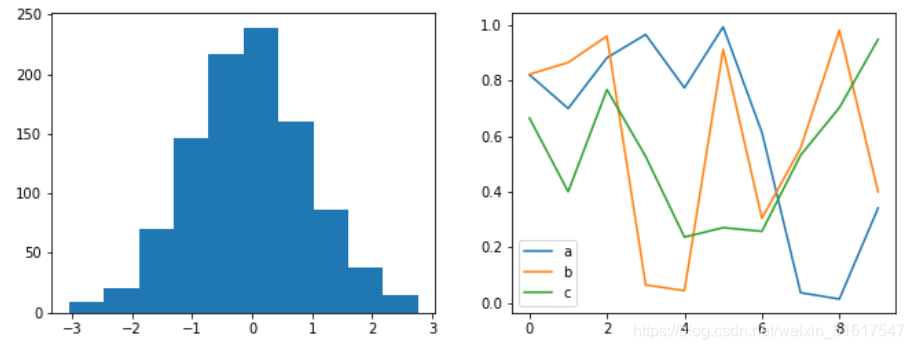
重置rcParams之后,即是默认风格,默认风格简约直观,也是一种不错的选择。
2.FiveThirtyEight风格
FiveThirtyEight风格模仿的是网站.FiveThirtyEight的绘图风格,这种风格使用深色的粗线条和透明的坐标轴:
with plt.style.context('fivethirtyeight'):
hist_and_lines()
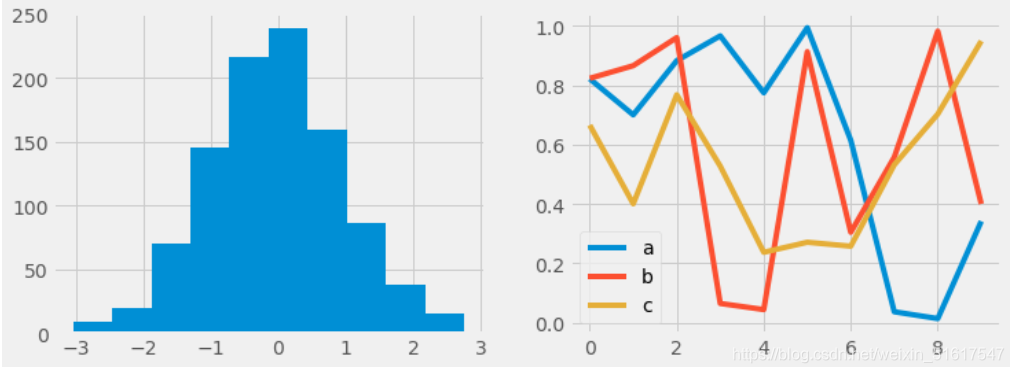
3.ggplot风格
ggplot风格是模仿R语言的ggplot可视化工具的默认风格。
with plt.style.context('ggplot'):
hist_and_lines()
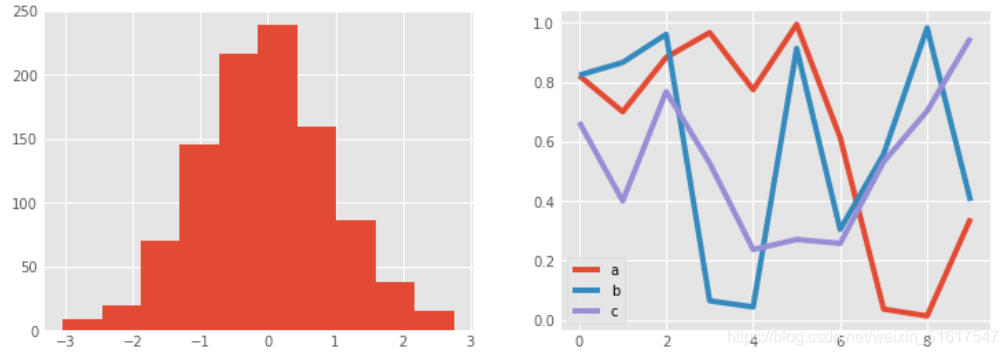
4.bmh风格
bmh风格继承了电子书Probabilistic Programming and Bayesian Methods for Hackers 中的绘图风格。
with plt.style.context('bmh'):
hist_and_lines()
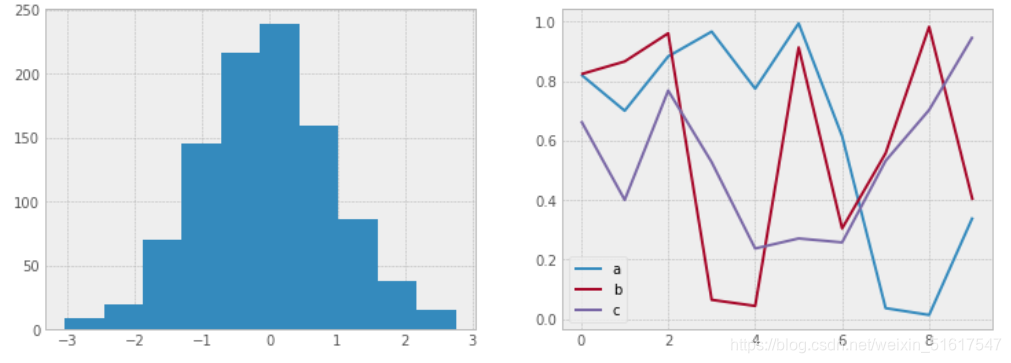
5.黑色背景风格
在演示文档中展示图形时,使用黑色的背景往往会有更好的效果。
with plt.style.context('dark_background'):
hist_and_lines()
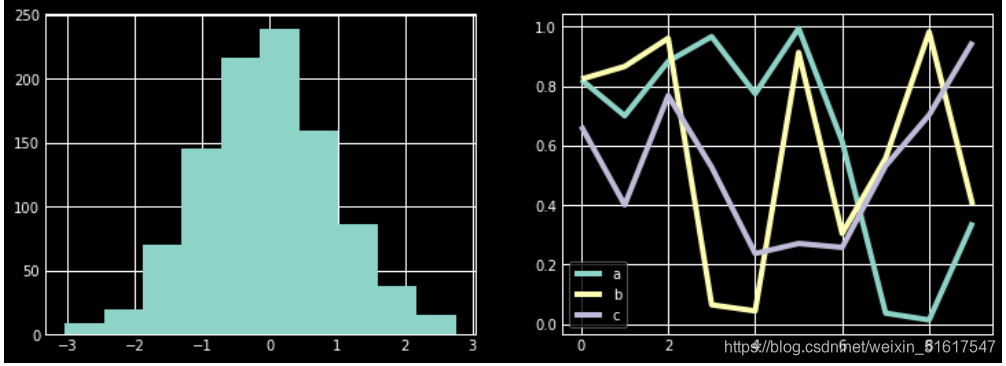
6.灰度风格
一种适合黑白打印的风格。
with plt.style.context('grayscale'):
hist_and_lines()
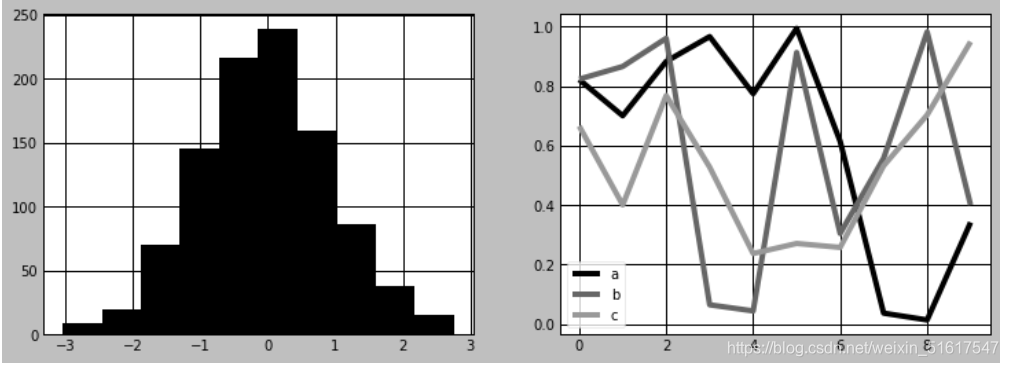
在不同的场景下灵活地使用不同的风格来绘图会让你的可视化锦上添花。
5.绘制三维图
首先引入Matplotlib中绘制三维图的工具
from mpl_toolkits import mplot3d
fig=plt.figure()
ax=plt.axes(projection='3d')
5.1 三维数据点与线
最基本的三维图是由(x,y,z)三维坐标点构成的线图与散点图。与前面介绍的普通二维图类似,可以用ax.plot3D与ax.scatter3D函数来创建它们。下面通过一个三角螺旋线和一些散点来举例:
ax=plt.axes(projection='3d')
zline=np.linspace(0,15,1000)
xline=np.sin(zline)
yline=np.cos(zline)
ax.plot3D(xline,yline,zline,'gray')
zdata=15*np.random.random(100)
xdata=np.sin(zdata)+0.1*np.random.randn(100)
ydata=np.cos(zdata)+0.1*np.random.randn(100)
ax.scatter3D(xdata,ydata,zdata,c=zdata,cmap='Greens')
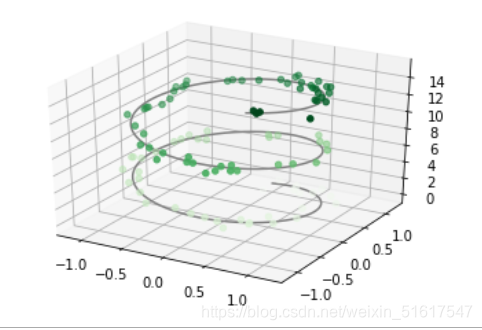
5.2 三维等高线图
与二维的ax.contour图形一样,ax.contour3D同样要求所有数据都是二维网格数据的形式,并且由函数计算z轴数值,下面演示一个用三维正弦函数画的三维等高线图:
def f(x,y):
return np.sin(np.sqrt(x**2+y**2))
x=np.linspace(-6,6,30)
y=np.linspace(-6,6,30)
X,Y=np.meshgrid(x,y)
Z=f(X,Y)
fig=plt.figure()
ax=plt.axes(projection='3d')
ax.contour3D(X,Y,Z,50,cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');
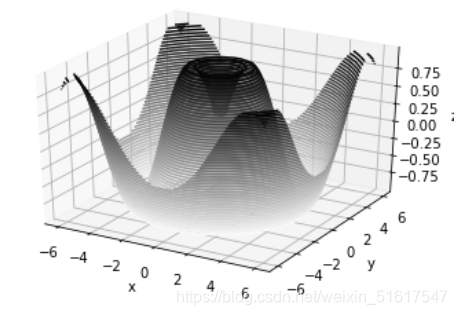
我们还可以通过ax.view_init()调整观察角度与方位角,我们现在将俯仰角调整为60度(即x-y平面的旋转角度为60°),方位角调整为35度(即绕z轴旋转35°):
ax.view_init(60,35)
fig
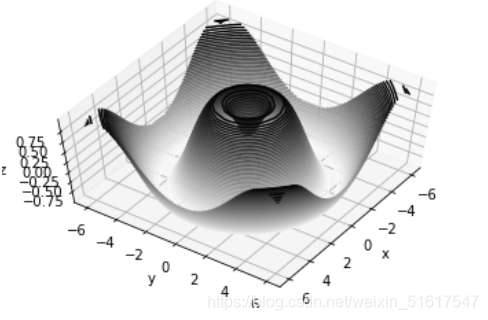
5.3 线框图与曲面图
接下来介绍另外两种画网格数据的三维图——线框图和曲面图。它们都是将网格数据映射成三维曲面,得到的三维形状非常容易可视化。下面是一个线框图示例:
fig=plt.figure()
ax=plt.axes(projection='3d')
ax.plot_wireframe(X,Y,Z,color='black');
ax.set_title('wireframe');
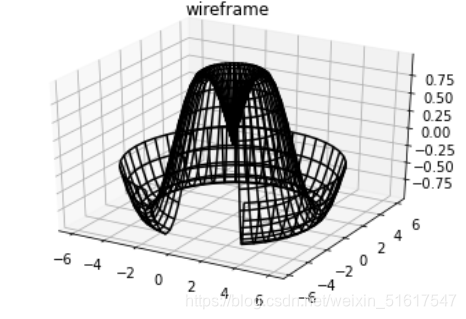
曲面图与线框图类似,只不过线框图的每个面都是由多边形构成的。只要增加一个配色方案来填充这些多边形,就可以让读者感受到可视化图形表面的拓扑结构了:
ax=plt.axes(projection='3d')
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap='viridis',edgecolor='none')
ax.set_title('surface');
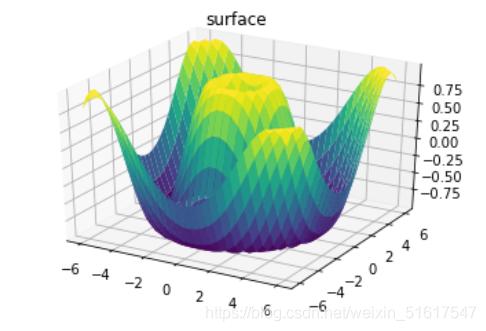
需要注意的是,曲面画图需要二维数据,但可以不是直角坐标系(可以用极坐标)。下面的示例创建了一个局部极坐标网格,当我们把它画成surface3D图形时,可以获得一种使用了切片的可视化效果:
r=np.linspace(0,6,20)
theta=np.linspace(-0.9*np.pi,0.8*np.pi,40)
r,theta=np.meshgrid(r,theta)
X=r*np.sin(theta)
Y=r*np.cos(theta)
Z=f(X,Y)
ax=plt.axes(projection='3d')
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap='viridis',edgecolor='none');
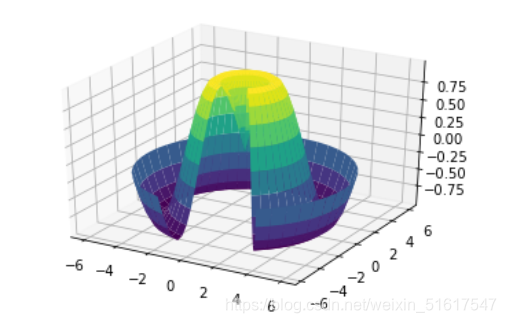
5.4 曲面三角剖分
我们首先创造一组随机数据,并生成对其的散点图:
theta=2*np.pi*np.random.random(1000)
r=6*np.random.random(1000)
x=np.ravel(r*np.sin(theta))
y=np.ravel(r*np.cos(theta))
z=f(x,y)
ax=plt.axes(projection='3d')
ax.scatter(x,y,z,cmap='viridis',linewidth=0.5);
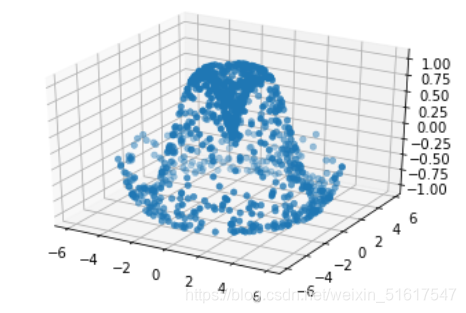
接下来我们通过使用ax.plot_trisurf()函数来帮助我们修补这个图形成为曲面图,它首先找到一组所有点都连接起来的三角形,然后用这些三角形创建曲面:
ax=plt.axes(projection='3d')
ax.plot_trisurf(x,y,z,cmap='viridis',edgecolor='none');
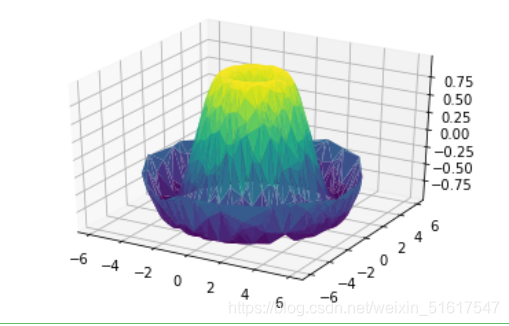
虽然这种方法绘制的图形肯定没有之前用均匀网格画的图完美,但是这种三角剖分方法非常灵活,可以创建各种有趣的三维图。例如,可以用它画一条莫比乌斯带:
theta=np.linspace(0,2*np.pi,30)
w=np.linspace(-0.25,0.25,8)
w,theta=np.meshgrid(w,theta)
phi=0.5*theta
r=1+w*np.cos(phi)
x=np.ravel(r*np.cos(theta))
y=np.ravel(r*np.sin(theta))
z=np.ravel(r*np.sin(phi))
from matplotlib.tri import Triangulation
tri=Triangulation(np.ravel(w),np.ravel(theta))
ax=plt.axes(projection='3d')
ax.plot_trisurf(x,y,z,triangles=tri.triangles,cmap='viridis',linewidth=0.2);
ax.set_xlim(-1,1);
ax.set_ylim(-1,1);
ax.set_zlim(-1,1);
6.用Basemap可视化地理数据
地理数据的可视化是数据科学中一种十分常见的可视化类型。Matplotlib做此类可视化的主要工具是Basemap工具箱,它是Matplotlib的mpl_toolkits命名空间里的众多工具箱之一。现在,我们将演示一些利用Basemap工具箱绘制地图的可视化示例。
安装好basemap程序包后,我们运行下面的代码:
from mpl_toolkits.basemap import Basemap
plt.figure(figsize=(8,8))
m=Basemap(projection='ortho',resolution=None,lat_0=50,lon_0=100)
m.bluemarble(scale=0.5);
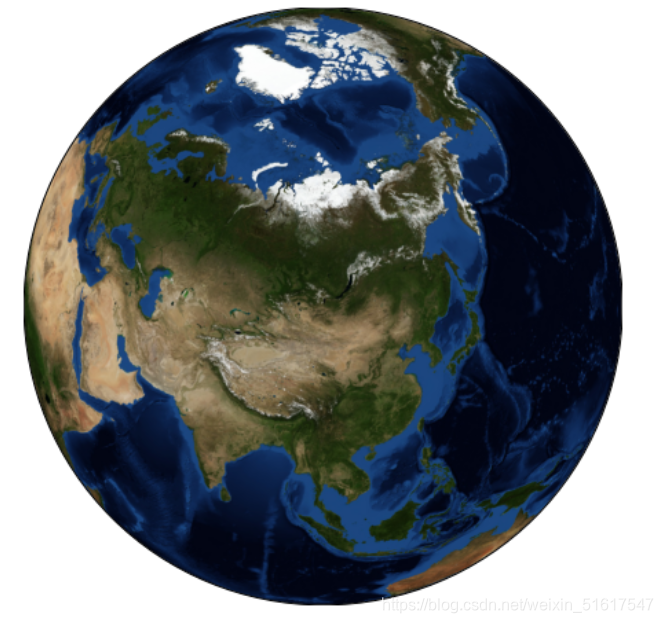
这里显示的地球并不是一个静止的图片,它是一个用球面坐标系构建的、功能齐全的Matplotlib坐标轴,可以轻易地在地图上增添数据。例如,我们可以将地图放大,并标出北京在地图上的位置:
fig=plt.figure(figsize=(8,8))
m=Basemap(projection='lcc',resolution=None,width=8E6,height=8E6,lat_0=50,lon_0=100)
m.etopo(scale=0.5,alpha=0.7)#显示陆地与海底的地形特征
#地图上的(经度,纬度)对应图上的(x,y)坐标
x,y=m(116,40)
plt.plot(x,y,'ok',markersize=5)
plt.text(x,y,'Beijing',fontsize=12)
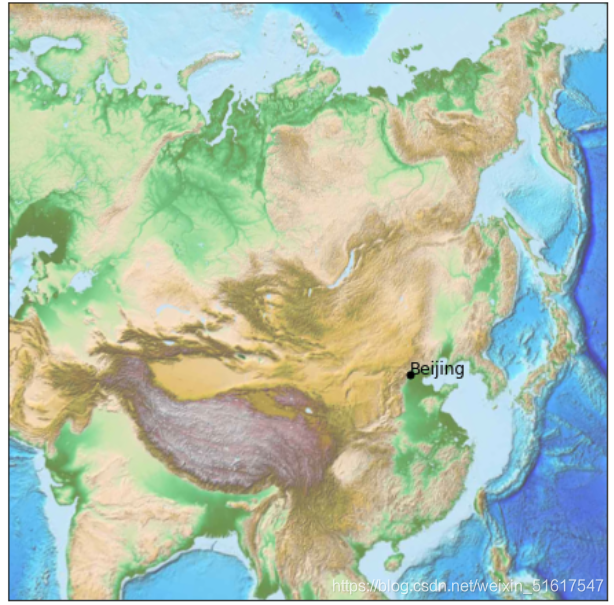
下面我们将深入介绍Basemap的主要特性,并通过一些可视化地图的示例来进行演示。
6.1 地图投影
首先定义一个可以画带经纬线地图的简便方法:
from itertools import chain
def draw_map(m,scale=0.2):
m.shadedrelief(scale=scale)
lats=m.drawparallels(np.linspace(-90,90,13))
lons=m.drawmeridians(np.linspace(-180,180,13))
lat_lines=chain(*(tup[1][0] for tup in lats.items()))
lon_lines=chain(*(tup[1][0] for tup in lons.items()))
all_lines=chain(lat_lines,lon_lines)
for line in all_lines:
line.set(linestyle='-',alpha=0.3,color='w')
1.圆柱投影
fig=plt.figure(figsize=(8,6),edgecolor='w')
m=Basemap(projection='cyl',resolution=None,llcrnrlat=-90,urcrnrlat=90,llcrnrlon=-180,urcrnrlon=180)
draw_map(m)
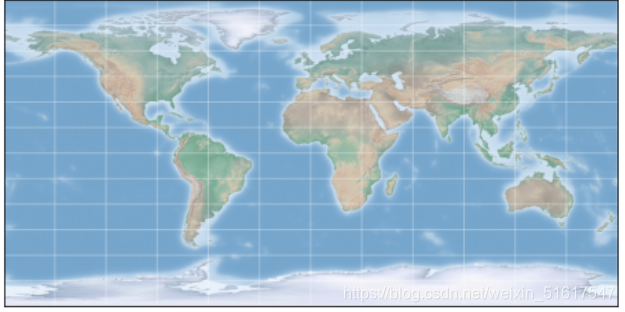
设置了左下角(llcrnr),右上角(urcrnr),纬度(lat)和经度(lon)的参数。
另外两种圆柱投影是墨卡托(projection='merc')投影和圆柱等积投影(projection='cea')。
2.伪圆柱投影
fig=plt.figure(figsize=(8,6),edgecolor='w')
m=Basemap(projection='moll',resolution=None,lat_0=0,lon_0=0)
draw_map(m)
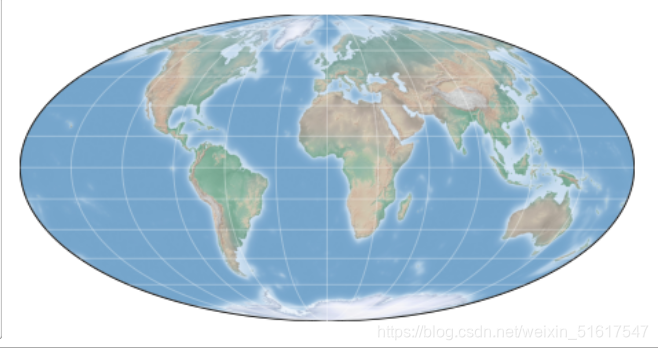
另外两种伪圆柱投影的类型是正弦(projection='sinu')投影与罗宾森(projection='robin')投影。
3.透视投影
正射投影:
fig=plt.figure(figsize=(8,8))
m=Basemap(projection='ortho',resolution=None,lat_0=50,lon_0=0)
draw_map(m);
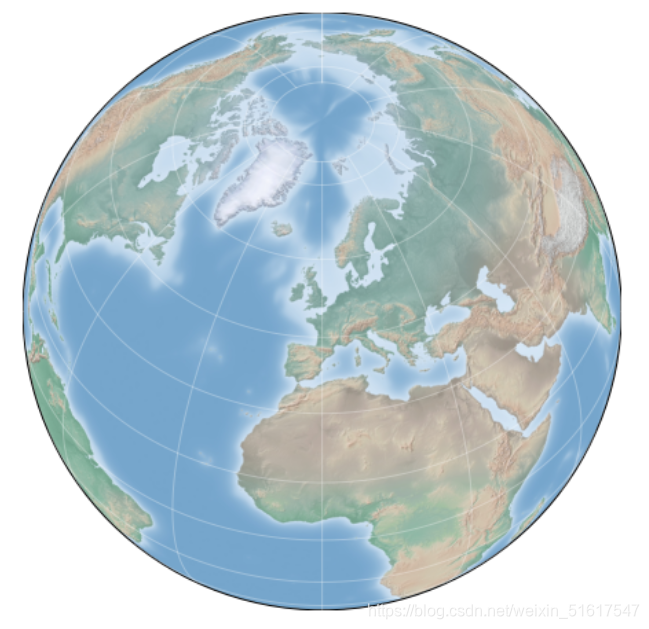
另外还有球心投影(projection='gnom')和球极平面(projection='stere')投影。
4.圆锥投影
兰勃特等角圆锥投影:
fig=plt.figure(figsize=(8,8))
m=Basemap(projection='lcc',lat_0=50,lon_0=0,resolution=None,lat_1=45,lat_2=55,width=1.6E7,height=1.6E7)
draw_map(m);
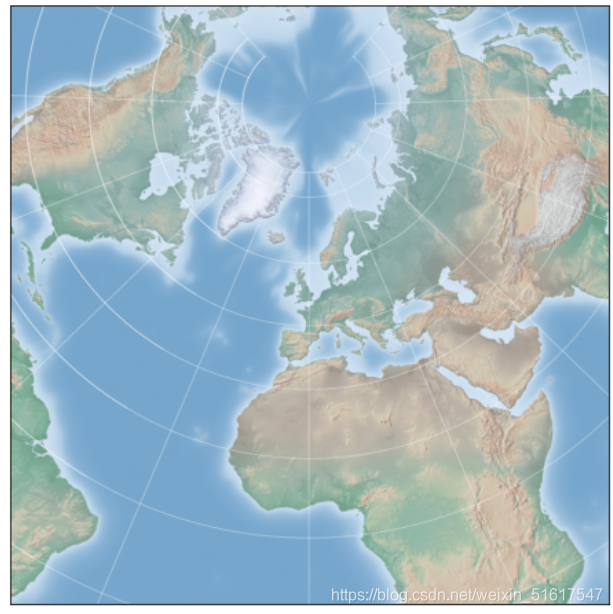
等距圆锥(projection='eqdc')投影和阿尔伯斯等积圆锥(projection='aea')投影。
圆锥投影和透视投影一样,适合显示较小与中等的地图。
6.2 绘制地图背景
下面给出Basemap中一些函数的用法:
| 函数名称 | 用途 |
|---|---|
| bluemarble()、shadedrelief() | 画出地球投影 |
| drawparallels()、drawmeridians() | 画出经线和纬线 |
| drawcoastlines() | 绘制大陆海岸线 |
| drawlsmask() | 为陆地和海洋设置填充色,从而可以在陆地或海洋投影其他图像 |
| drawmapboundary() | 绘制地图边界,包括为海洋填充颜色 |
| drawrivers() | 绘制河流 |
| fillcontinents() | 用一种颜色填充大陆,另一种颜色填充湖泊(可选) |
| drawcountries() | 绘制国界线 |
| drawgreatcircle() | 在两点之间绘制一个大圆 |
| drawparallels() | 绘制纬线 |
| drawmeridians() | 绘制经线 |
| drawmapscale() | 在地图上绘制一个线性比例尺 |
| etopo() | 在地图上绘制地形晕渲图 |
| warpimage() | 将用户提供的图像投影到地球上 |
如果要使用边界特征,就必须在创建Basemap图形时设置分辨率。Basemap类提供了resolution参数来设置边界的分辨率,分为’c’(原始分辨率),‘l’(低分辨率),‘i’(中等分辨率),‘h’(高分辨率),‘f’(全画质分辨率),如果不使用边界线则设置为None,这个参数的设置决定了图形渲染的速度。
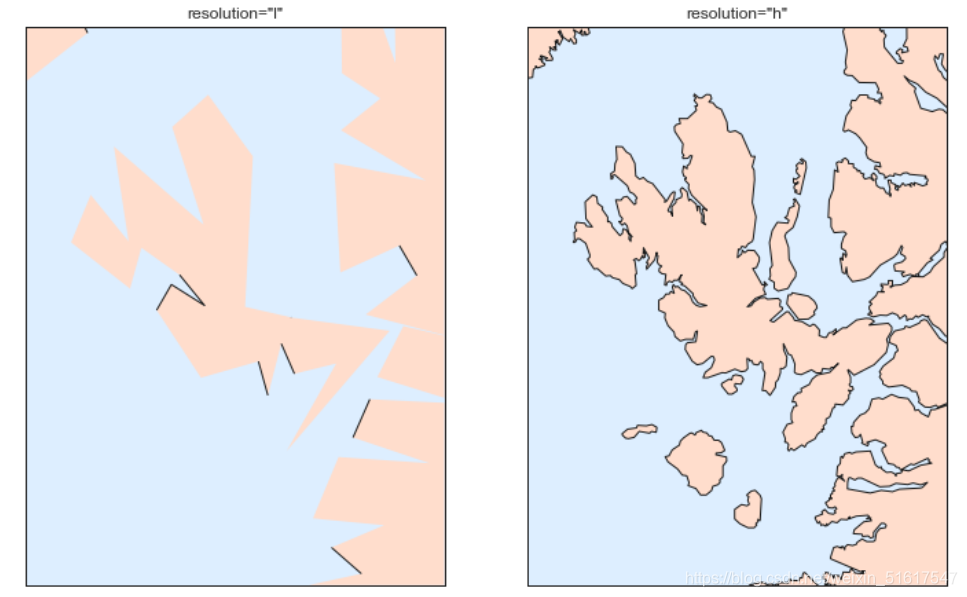
下面举一个例子,对比不同的渲染效果:
fig,ax=plt.subplots(1,2,figsize=(12,8))
for i,res in enumerate(['l','h']):
m=Basemap(projection='gnom',lat_0=57.3,lon_0=-6.2,width=90000,height=120000,resolution=res,ax=ax[i])
m.fillcontinents(color='#FFDDCC',lake_color='#DDEEFF')
m.drawmapboundary(fill_color='#DDEEFF')
m.drawcoastlines()
ax[i].set_title('resolution="{0}"'.format(res));
7.Seaborn数据可视化
首先,我们对Matplotlib的传统样式与Seaborn样式进行一个简单的对比:
rng=np.random.RandomState(0)
x=np.linspace(0,10,500)
y=np.cumsum(rng.randn(500,6),0)
plt.plot(x,y)
plt.legend('ABCDEF',ncol=2,loc='upper left');
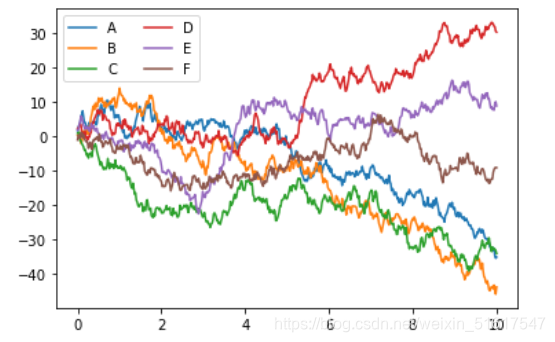
import seaborn as sns
sns.set()
plt.plot(x,y)
plt.legend('ABCDEF',ncol=2,loc='upper left');
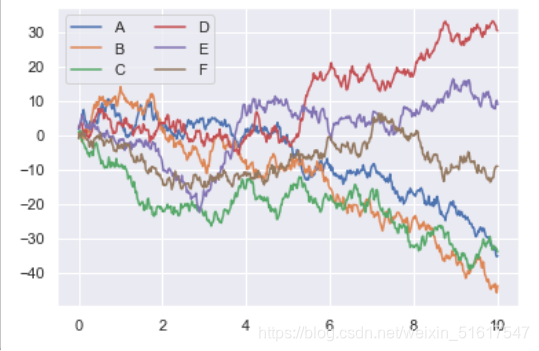
可以看到,Seaborn使用的默认风格和参数的效果会比传统的Matplotlib的格式要好一些。
下面我们来介绍一些Seaborn中常见的图形绘制方法。
1.频次直方图、KDE和密度图
频次直方图:
data=np.random.multivariate_normal([0,0],[[5,2],[2,2]],size=2000)
data=pd.DataFrame(data,columns=['x','y'])
for col in 'xy':
plt.hist(data[col],alpha=0.5)
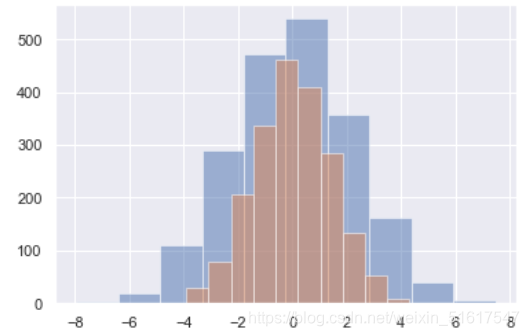
KDE图:
for col in 'xy':
sns.kdeplot(data[col],shade=True)
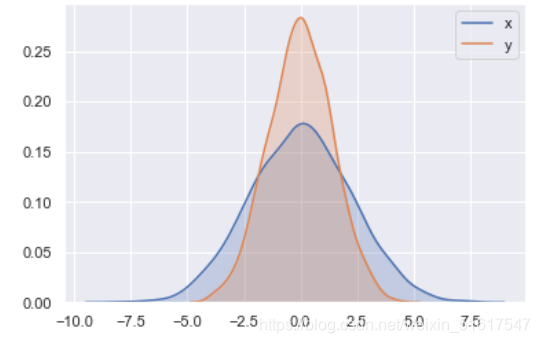
我们可以使用distplot()函数让二者结合:
sns.distplot(data['x'])
sns.distplot(data['y']);
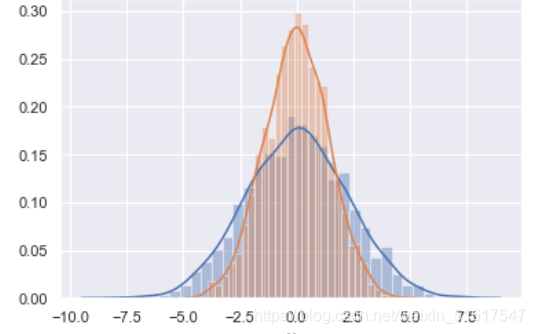
如果向kdeplot输入的是一个二维数据集,那么就可以获得一个二维数据可视化图:
sns.kdeplot(data);
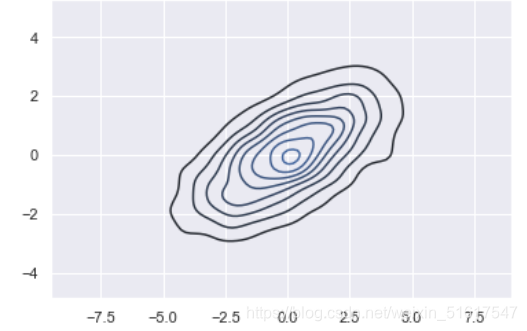
用sns.jointplot()可以同时看到两个变量的联合分布与单变量的独立分布。在这个图形中,使用白色背景:
with sns.axes_style('white'):
sns.jointplot('x','y',data,kind='kde');
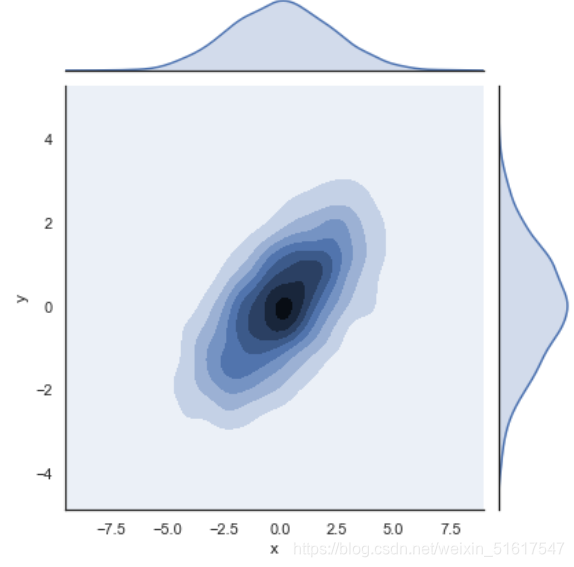
可以向jointplot函数传递一些参数,例如,可以用六边形块代替频次直方图:
with sns.axes_style('white'):
sns.jointplot('x','y',data,kind='hex');
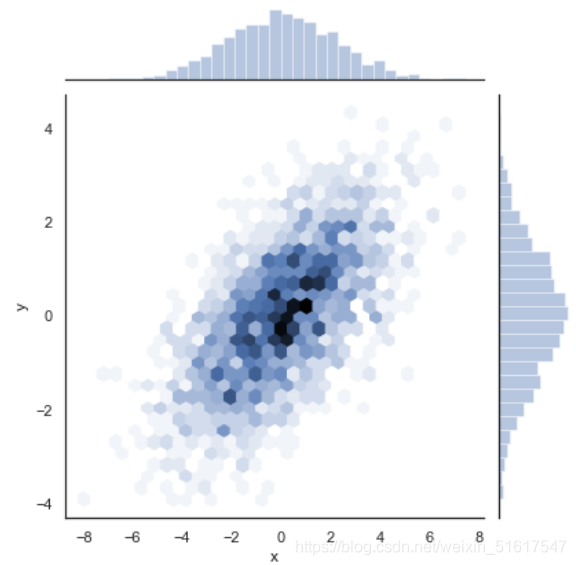
2.矩阵图
当需要对多维数据集进行可视化时,最终都要使用矩阵图(pair plot),如果想画出所有变量中任意两个变量之间的图形,用矩阵图探索多维数据不同维度间的相关性非常有效。
下面我们使用鸢尾花数据集来演示:
iris=sns.load_dataset('iris')
sns.pairplot(iris,hue='species',size=2.5);
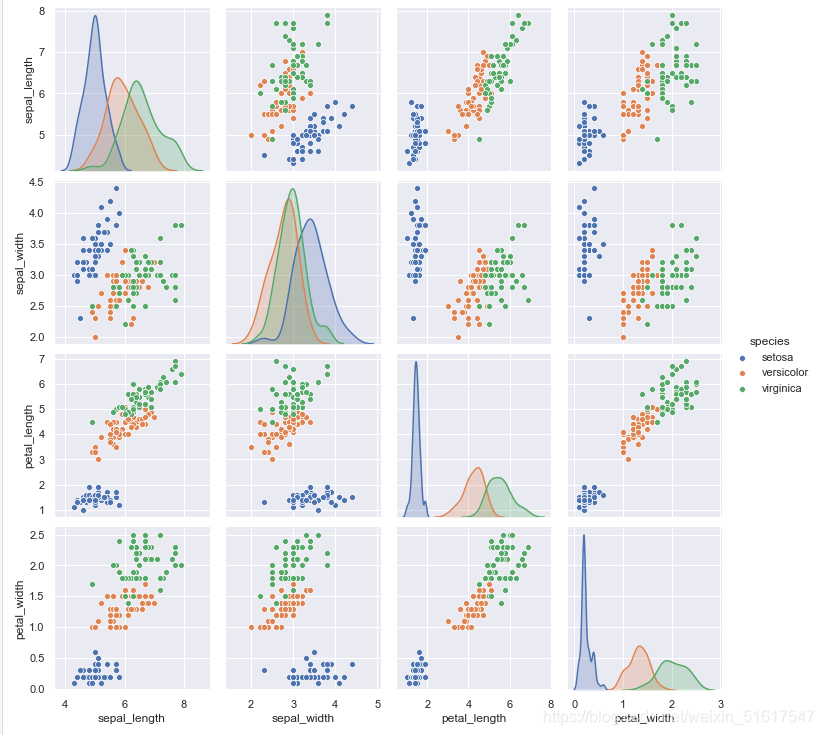
3.分面频次直方图
有时观察数据最好的方法就是借助数据子集的频次直方图。Seaborn的FacetGrid()函数可以绘画这样的图形。
tips=sns.load_dataset('tips')
tips['tip_pct']=100*tips['tip']/tips['total_bill']
grid=sns.FacetGrid(tips,row='sex',col='time',margin_titles=True)
grid.map(plt.hist,'tip_pct',bins=np.linspace(0,40,15));
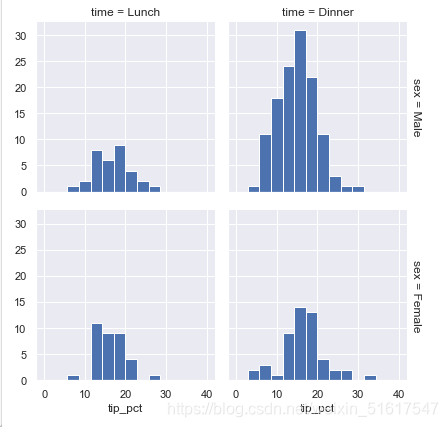
4.因子图
因子图(factor plot)也是对数据子集进行可视化的方法,我们可以通过观察一个参数在另一个参数间隔中的分布情况:
with sns.axes_style(style='ticks'):
g=sns.factorplot('day','total_bill','sex',data=tips,kind='box')
g.set_axis_labels('Day','Total Bill');
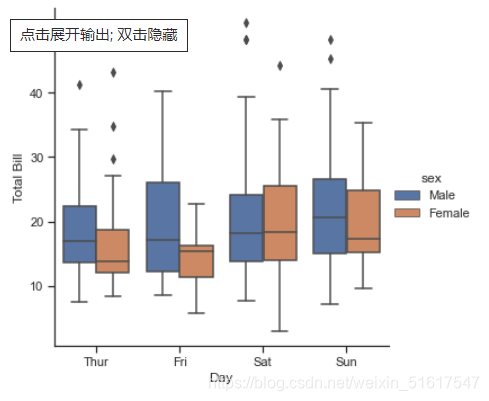
5.联合分布图
与矩阵图类似,可以用sns.jointplot()画出不同数据集的联合分布和各数据本身的分布:
with sns.axes_style('white'):
sns.jointplot('total_bill','tip',data=tips,kind='hex')
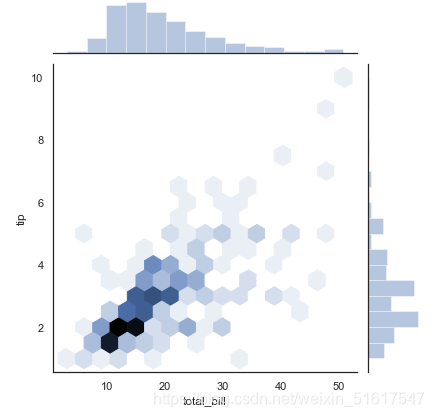
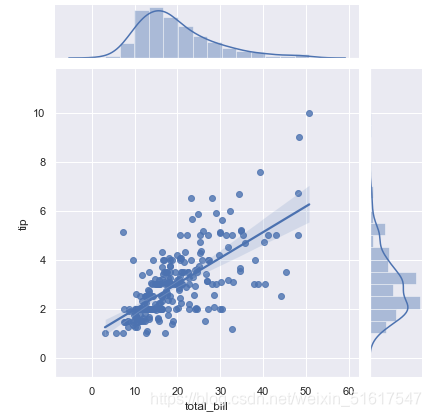
联合分布图也可以自动进行KDE与回归:
sns.jointplot('total_bill','tip',data=tips,kind='reg');
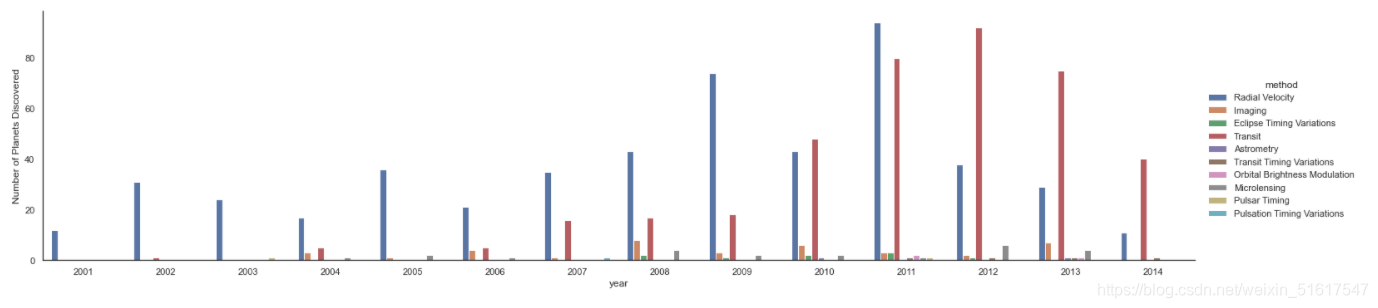
6.条形图
planets=sns.load_dataset('planets')
with sns.axes_style('white'):
g=sns.factorplot('year',data=planets,aspect=4,kind='count',hue='method',order=range(2001,2015))
g.set_ylabels('Number of Planets Discovered')
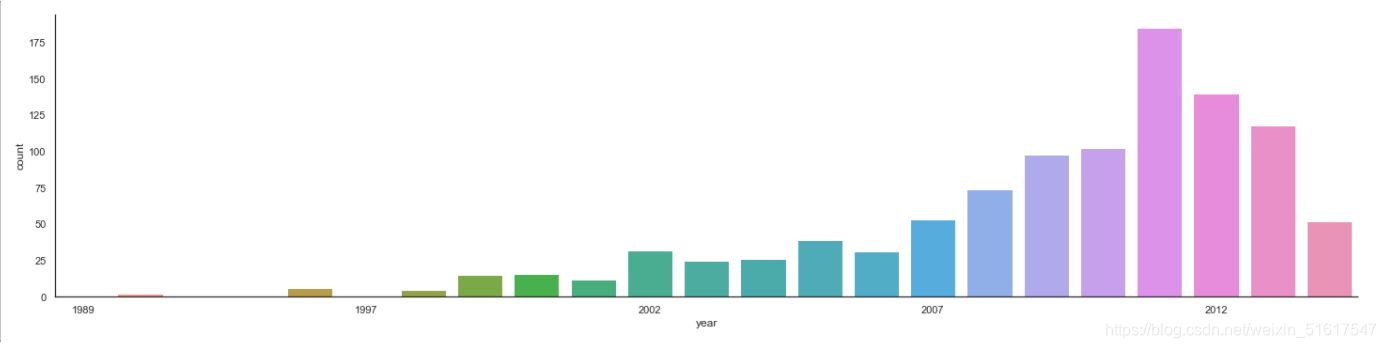
with sns.axes_style('white'):
g=sns.factorplot('year',data=planets,aspect=4,kind='count')
g.set_xticklabels(step=5)
到此,本章的内容就全部结束了,希望对各位能有所帮助。