Python小白的数学建模课-21.关键路径法
- 关键路径法是基于进度网络模型的方法,用网络图表示各项活动之间的相互关系,获得在一定工期、成本、资源约束条件下的最优进度安排。
- NetworkX 提供了拓扑序列和关键路径的函数,但没有给出计划网络分析的时间参数,如事件的最早开工时间、最晚结束时间,因此不能实现对计划网络图的分析和优化。
- 本文的案例给出了关键路径算法的完整例程,并同时计算事件的最早开工时间、最晚完成时间,以便读者使用。
- 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。
1. 关键路径法简介
一个大型工程或项目包括很多活动,关键路径是项目中时间最长的活动顺序,决定着可能的项目最短工期。
关键路径法(Critical path method,CPM) 是一种基于进度网络模型的方法,用网络图表示各项活动之间的相互关系,获得在一定工期、成本、资源约束条件下的最优进度安排。
关键路径法源于美国杜邦公司对于项目管理控制成本、减少工期的研究。1959年,Kelly 和 Walker 在论文 Critical Path Planning and Scheduling 中提出了关键路径法的基本原理和方法:计算所有活动的工期,确定其最早开始 ES 和最早结束 EF、最晚开始 LS 和最晚结束 LF 的时间,按照活动的相互关系形成顺序的网络逻辑 图,找到必须的最长路径即为关键路径。
关键路径法将项目分解成为多个独立的活动并确定每个活动的工期,然后用逻辑关系(结束-开始、结束-结束、开始-开始和开始-结束)将活动连接。首先使用正推法(Forward pass),从起点开始向后计算,依次计算每个顶点(事件)的最早开始时间 ES;然后再使用逆推法(Backward pass),从终点开始向前计算,依次计算每个顶点(事件)的最迟结束时间 LF。进而可以求出每条边(工序)的最早结束时间 EF 和最迟开始时间 LS。最早开始时间 ES 和最晚开始时间 LS 相等的边,就是关键路径上的边,对应的工序是关键工序。
- ES:最早开始时间(Earliest Start),指某项活动能够开始的最早时间,取决于该项活动的所有紧前工作的结束时间,由顺推法计算 ES = max{EF(preceding activities)}。
- EF:最早结束时间(Earliest Finish),指某项活动能够完成的最早时间。EF = ES+DU, DU为该活动的持续时间。
- LF:最迟结束时间(Latest Finish),指为了保证整个项目按期完成的某项活动必须完成的最晚时间,取决于该项活动的所有紧后工作的最迟开始时间,由逆推法计算 LF = min{LS(successor activities)}。
- LS:最迟开始时间(Latest Start),指为了保证整个项目按期完成的某项活动必须开始的最迟时间。LS = LF -DU,DU为该活动的持续时间。
- TF:总时差(Total float time),指在不影响总工期的条件下,一个活动可以利用的机动时间。TF = LF - EF。
- FF:自由时差(Free float time),指在不影响紧后工作最早开始时间的条件下,一个活动可能被延迟的时间。FF = min{ES(successor activities)} - EF。
由关键路径法得到的最早/最晚的开始/结束时间并不一定就是项目进度计划,而是把既定的参数(活动持续时间、逻辑关系、提前量、滞后量和其它制约条件)输入进度模型后所得到的结果,表明活动可以在该时段内实施。
早期关键路径法的表示方法都是箭线法(ADM),随着计算机的发展,前导图(PDM)逐渐成为主流方法。
2. 拓扑序列与关键路径
2.1 拓扑序列
大型项目包括很多子项目,有些子项目没有先决条件,可以安排在任何时间开始,有些子项目必须安排在其它子项目完成后才能开始,也就是需要以所有前序子项目的结束为先决条件。
通过有向图可以直观反映项目中各个子项目之间的关系。图中的顶点代表活动,有向边代表活动的先后关系。有向边的起点活动是终点活动的先决条件,只有当边的起点活动完成之后,才能开始终点活动。
这种以顶点表示活动、边表示活动间先后关系的有向图,称为顶点活动网(Activity on vertex network,AOV网)。
AOV网是一个有向无环图,即不存在回路。有向无环图的所有活动可排列成一个线性序列,使每个活动的所有前驱活动都排在该活动之前,称为拓扑序列(Topological order)。
拓扑序列的意义是,如果按照拓扑序列中的顶点次序开始活动,每个活动开始时它的所有前驱活动都已完成,从而使整个工程得以顺序进行。
AOV 网和拓扑序列只考虑网络拓结构,也就是只有各个活动的先后顺序,不考虑活动所需的时间和费用。因此,AOV 网的拓扑序列通常不是唯一的,而只是各种可行顺序之一。
2.2 活动网络
**带权的活动网络(Activity on edge network,AOE网),顶点表示事件或状态,有向边表示活动,边上的权值通常表示活动的持续时间。**AOE网可以用来估算项目的完成时间。
注意 AOV网与 AOE网的区别,不仅在于边是否带权。AOV网的顶点代表活动(工序), 边只表示先后关系;AOE网的顶点表示事件,边表示工序,边的权值表示完成工序所需的时间。
**AOE 网中从起点到终点的最长的加权路径长度,称为关键路径(Critical path,CP) 。**关键路径是项目中时间最长的活动顺序,决定着可能的项目最短工期 。优化关键路径可以有效地加快设工程实施的进度。
3. NetworkX 的拓扑序列和关键路径算法
NetworkX 提供了有向无环图的拓扑序列和关键路径的函数。
3.1 拓扑序列函数 topological_sort()
| 函数 | 功能 |
|---|---|
| topological_sort(DG) | 返回按拓扑排序的节点生成器 |
| all_topological_sorts(DG) | 返回所有按拓扑排序的节点生成器 |
| is_directed_acyclic_graph(DG) | 检查 DG 是否为有向无环图 |
topological_sort(DG) 返回有向无环图 DG 的一个拓扑序列,返回值的类型为 <class ‘generator’>,可以转化为列表类型方便使用。
有向无环图 DG 的拓扑序列不是唯一的,all_topological_sorts(DG) 返回有向无环图 DG 的全部拓扑序列,返回值的类型为 <class ‘generator’>,可以转化为二维列表类型方便使用。
如果 DG 不是有向图,函数抛出错误提示"NetworkXNotImplemented"。如果 DG 不是无环图,函数抛出错误提示"NetworkXUnfeasible"。
is_directed_acyclic_graph(DG) 可以检查 DG 是否为有向无环图。当 DG 为有向无环图时,返回值为 True,否则返回 False。
3.2 关键路径和路径长度函数 dag_longest_path()
| 函数 | 功能 |
|---|---|
| dag_longest_path(DG) | 返回 DG 的最长路径 |
| dag_longest_path_length(DG) | 返回 DG 的最长路径长度 |
dag_longest_path(G, weight=‘weight’, default_weight=1, topo_order=None)
dag_longest_path_length(G, weight=‘weight’, default_weight=1)
主要参数:
- G(NetworkX graph):有向无环图。
- weight (str, optional):按该字符串查找边的属性作为权重。默认值 weight=“weight”。
返回值:
- dag_longest_path() 的返回值是 DG 最长路径的顶点列表,也即关键路径的节点列表。
- dag_longest_path_length() 的返回值是 DG 最长路径的组成边的加权长度,也即关键路径的长度。
参数和返回值都非常简单,用起来是很方便的。但是,NetworkX 工具包没有提供计划网络分析所需的事件时间参数,因此不能进行网络优化。
3.3 Python 例程:关键路径法
问题描述:
某项目工程由 11项作业组成(分别用 A、B、…K表示),其计划完成时间及作业间相互关系如下表所示。建立计划网络图,并计算完成该项目的最短时间。
| 作业 | 计划完成天数 | 紧前工序 | 作业 | 计划完成天数 | 紧前工序 |
|---|---|---|---|---|---|
| A | 5 | 无 | G | 21 | B,E |
| B | 10 | 无 | H | 35 | B,E |
| C | 11 | 无 | I | 25 | B,E |
| D | 4 | B | J | 15 | F,G,I |
| E | 4 | A | K | 20 | F,G |
| F | 15 | C,D |
本案例问题来自:司守奎、孙兆亮,数学建模算法与应用(第2版),P62-68,例4.16-4.18,国防工业出版社。
问题分析:
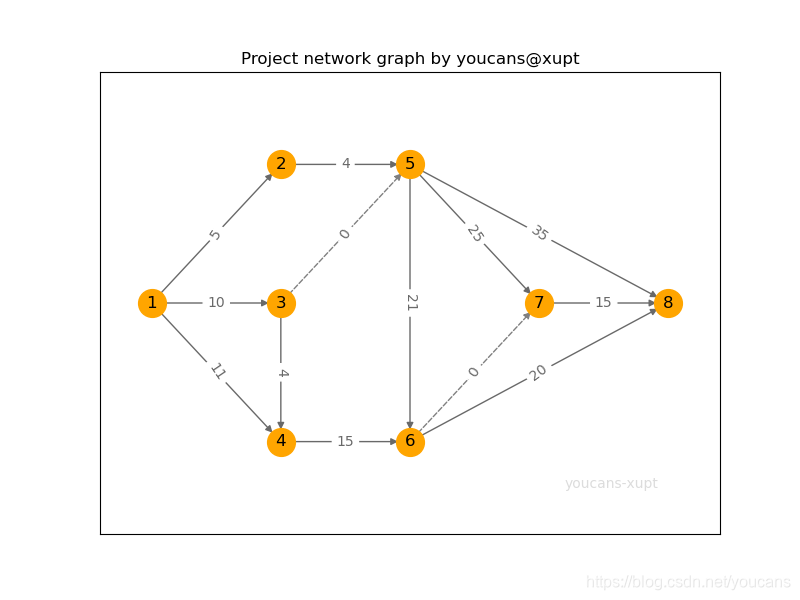
用如下图所示的计划网络图表示问题描述的各项作业及作业间的相互关系。图中的顶点表示作业开始或结束的事件,顶点之间的边(箭线)表示一项作业,边的权值表示该项作业的完成时间。虚线边表示虚拟作业。
该计划网络图的关键路径长度,即为完成该项目的最短时间。
Python 例程:
# mathmodel23_v1.py
# Demo20 of mathematical modeling algorithm
# Demo of critical path method (CPM) with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated:2021-07-25
import numpy as np
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx # 导入 NetworkX 工具包
# 1. 拓扑序列(topological sequence) 和 关键路径(critical path)
# Activity on edge network(AOE), 顶点表示事件或状态,有向边表示活动
DG = nx.DiGraph() # 创建:空的 有向图
DG.add_weighted_edges_from([(1, 2, 5), (1, 3, 10), (1, 4, 11),
(2, 5, 4),
(3, 4, 4), (3, 5, 0),
(4, 6, 15),
(5, 6, 21), (5, 7, 25), (5, 8, 35),
(6, 7, 0), (6, 8, 20),
(7, 8, 15)]) # 向图中添加多条赋权边: (n1,n2,weight)
lenNodes = len(DG.nodes) # 顶点数量
topoSeq = list(nx.topological_sort(DG)) # 拓扑序列
nodeCP = list(nx.dag_longest_path(DG)) # 关键路径(节点)
lenCP = nx.dag_longest_path_length(DG) # 关键路径的长度
edgesCP=[]
for k in range(1,len(nodeCP)):
edgesCP.append((nodeCP[k-1],nodeCP[k]))
print("拓扑序列:{}".format(topoSeq)) # [1, 3, 4, 2, 5, 6, 7, 8]
print("关键路径的顶点:{}".format(nodeCP)) # [1, 3, 5, 6, 8]
print("关键路径的边:{}".format(edgesCP)) # [(1, 3), (3, 5), (5, 6), (6, 8)]
print("关键路径长度:{}".format(lenCP)) # 51
fig, ax = plt.subplots(figsize=(8,6))
pos = {1:(0,4), 2:(5,7), 3:(5,4), 4:(5,1), 5:(10,7), 6:(10,1), 7:(15,4), 8:(20,4)} # 指定顶点位置
edgesDG = DG.edges
edgesDashed = [(3,5),(6,7)]
edgesSolid = list(set(edgesDG)-set(edgesDashed))
labels = nx.get_edge_attributes(DG, 'weight')
# nx.draw(DG, pos, with_labels=True, node_color='skyblue') # 绘制有向图
nx.draw_networkx_nodes(DG, pos, node_color='orange',node_size=400) # 设置指定顶点的颜色、宽度
nx.draw_networkx_labels(DG, pos) # 设置指定顶点的标签
nx.draw_networkx_edges(DG, pos, edgelist=edgesSolid, edge_color='dimgrey', style='solid') # 设置指定边的颜色、线型
nx.draw_networkx_edges(DG, pos, edgelist=edgesDashed, edge_color='grey', style='dashed') # 设置指定边,虚线
nx.draw_networkx_edge_labels(DG, pos, edge_labels=labels, font_color='dimgrey') # 显示边的权值
ax.set_title("Project network graph by youcans@xupt")
ax.text(16, 0, "youcans-xupt", color='gainsboro')
plt.xlim(-2, 22)
plt.ylim(-1, 9)
plt.axis('on')
plt.show() # YouCans, XUPT
程序运行结果:
拓扑序列:[1, 3, 4, 2, 5, 6, 7, 8]
关键路径的顶点:[1, 3, 5, 6, 8]
关键路径的边:[(1, 3), (3, 5), (5, 6), (6, 8)]
关键路径长度:51
4. 案例:计划网络分析与优化
4.1 问题描述
本案例问题的内容与本文 3.3 中案例相同。
某项目工程由 11项作业组成(分别用 A、B、…K表示),其计划完成时间及作业间相互关系如下表所示。求该项目的关键路径,并计算每项作业的最早开工时间 ES、最晚开工时间 LS。
4.2 问题分析
NetworkX 虽然提供了拓扑序列和关键路径的函数,但是没有给出网络分析所需的时间参数,如事件的最早开工时间、最晚完成时间,不能实现对计划网络图的分析和优化。
网络上关于计划网络图的分析与优化的 Python 语言例程不多,有的例程并不正确或者并没有调通,有的例程并不完整不能直接使用。
作者详细研究了 NetworkX 相关内容的说明文档,发现官方文档及例程也有问题,主要是由于 NetworkX 版本更新导致文档不匹配。
为此,本文的案例给出了关键路径算法的完整例程,并同时计算事件的最早开工时间、最晚完成时间,以便读者使用。
为了便于阅读、使用和修改程序,本程序采用了比较简单易读的程序结构——一些地方原本可以写的更简练。
4.3 程序说明
- AOE 图的输入。本例为稀疏的带权有向图,使用 G.add_weighted_edges_from() 函数可以使用列表向图中添加多条赋权边,每个赋权边以元组 (node1,node2,weight) 表示。
- 图中的顶点表示事件(状态),边表示问题中的作业工序,边的权值表示完成作业所需的时间。注意,(3, 5, 0),(6, 7, 0) 表示虚作业,完成该作业所需时间(资源)为0,只是表示工序的前后关系。
- nx.topological_sort(DG) 生成一个拓扑序列。
- for e in DG.in_edges(topoSeq[i]) 表示遍历顶点 topoSeq[i] 的入边,由此可以得到其所有相邻的前向顶点,各前向顶点的最早开始时间与连接边的权值之和 VEij 最大者即为该顶点的最早开始时间。顶点的最早开始时间,要从起点开始,依次向后计算,直到终点结束。
- for e in DG.out_edges(revSeq[i]) 表示遍历顶点revSeq[i] 的出边,由此可以得到其所有相邻的后向顶点,各后向顶点的最晚开始时间与连接边的权值之差 VLij 最小者即为该顶点的最晚开始时间。顶点的最晚开始时间,要从终点开始,依次向前计算,直到起点结束。
- 各条边(作业工序)的最早开始时间,是这条边的起点的最早开始时间。各条边(作业工序)的最晚开始时间,是这条边的终点的最晚开始时间减去边的权值。
- 关键路径的计算:如果一条边的最早、最晚开工时间相同,则这条边是关键路径上的边。
4.4 Python 程序
# mathmodel23_v1.py
# Demo23 of mathematical modLSing algorithm
# Demo of critical path method (CPM) with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated:2021-07-26
import numpy as np
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx # 导入 NetworkX 工具包
# 2. 关键路径的时间参数(critical path method)
DG = nx.DiGraph() # 创建:空的 有向图
# Activity on edge network(AOE), 顶点表示事件或状态,有向边表示活动
DG.add_nodes_from(range(1, 8), VE=0, VL=0)
DG.add_weighted_edges_from([(1, 2, 5), (1, 3, 10), (1, 4, 11),
(2, 5, 4),
(3, 4, 4), (3, 5, 0),
(4, 6, 15),
(5, 6, 21), (5, 7, 25), (5, 8, 35),
(6, 7, 0), (6, 8, 20),
(7, 8, 15)]) # 向图中添加多条赋权边: (node1,node2,weight)
lenNodes = len(DG.nodes) # 顶点数量 YouCans
topoSeq = list(nx.topological_sort(DG)) # 拓扑序列: [1, 3, 4, 2, 5, 7, 6, 8]
# --- 计算各顶点的 VE:事件最早时间 ---
VE = [0 for i in range(lenNodes)] # 初始化 事件最早时间
for i in range(lenNodes):
for e in DG.in_edges(topoSeq[i]): # 遍历顶点 topoSeq[i] 的 入边
VEij = DG.nodes[e[0]]["VE"] + DG[e[0]][e[1]]["weight"] # 该路线的最早时间
if VEij > VE[i]: VE[i] = VEij # 该路线所需时间更长
DG.add_node(topoSeq[i], VE=VE[i]) # 顶点(事件)的最早时间
# --- 计算各顶点的 VL:事件最晚时间 ---
revSeq = list(reversed(topoSeq)) # 翻转拓扑序列,以便从终点倒推计算 VL
VL = [DG.nodes[revSeq[0]]["VE"] for i in range(lenNodes)] # 初始化 事件最晚时间为 VE 最大值
for i in range(lenNodes):
for e in DG.out_edges(revSeq[i]): # 遍历顶点 revSeq[i] 的 出边
VLij = DG.nodes[e[1]]["VL"] - DG[e[0]][e[1]]["weight"] # 该路线的最晚时间
if VLij < VL[i]: VL[i] = VLij # 该路线所需时间更长
DG.add_node(revSeq[i], VL=VL[i]) # 顶点(事件)的最晚时间
print("\n顶点(事件)的最早时间 VE, 最晚时间 VL:")
for n in DG.nodes: # 遍历有向图的顶点
print("\t事件 {}:\tVE= {}\tVL= {}".format(n, DG.nodes[n]["VE"], DG.nodes[n]["VL"]))
# --- 计算各条边的 ES, LS:各项活动的最早开始时间、最晚开始时间 ---
cpDG = nx.DiGraph() # 创建空的有向图, 保存关键路径
print("\n边(活动)的最早开始时间 ES, 最晚开始时间 LS:")
for e in DG.edges: # 遍历有向图的边
DG[e[0]][e[1]]["ES"] = DG.nodes[e[0]]["VE"] # 边的头顶点的 VE
# Wij = DG[e[0]][e[1]]['weight']
DG[e[0]][e[1]]["LS"] = DG.nodes[e[1]]["VL"] - DG[e[0]][e[1]]["weight"] # 边的尾顶点的 VL 减去边的权值
if DG[e[0]][e[1]]["ES"] == DG[e[0]][e[1]]["LS"]: # 如果最早、最晚开工时间相同,则为关键路径上的边
cpDG.add_edge(e[0], e[1], weight=DG[e[0]][e[1]]["weight"]) # 加入 关键路径
# print("\t作业 {}:\tES= {}\tLS= {}".format(e, DG[e[0]][e[1]]["ES"], DG[e[0]][e[1]]["LS"]))
print("\t作业 {}:\tES= {}\tLS= {}\tDU= {}".format(e, DG[e[0]][e[1]]["ES"], DG[e[0]][e[1]]["LS"], DG[e[0]][e[1]]["weight"]))
lenCP = sum(cpDG[e[0]][e[1]]["weight"] for e in cpDG.edges)
print("\n关键路径:{}".format(cpDG.edges)) # YouCans, XUPT
print("项目最短工期:{}".format(lenCP))
# 绘制有向网络图
fig, ax = plt.subplots(figsize=(8,6))
pos = {1:(0,4), 2:(5,7), 3:(5,4), 4:(5,1), 5:(10,7), 6:(10,1), 7:(15,4), 8:(20,4)} # 指定顶点位置
edgesDG = DG.edges
edgesDashed = [(3,5),(6,7)]
edgesSolid = list(set(edgesDG)-set(edgesDashed))
labels = nx.get_edge_attributes(DG, "weight") # YouCans, XUPT
nx.draw_networkx_nodes(DG, pos, node_color='orange',node_size=400) # 设置指定顶点的颜色、宽度
nx.draw_networkx_labels(DG, pos) # 设置指定顶点的标签
nx.draw_networkx_edges(DG, pos, edgelist=edgesSolid, edge_color='dimgrey', style='solid') # 设置指定边的颜色、线型
nx.draw_networkx_edges(DG, pos, edgelist=edgesDashed, edge_color='grey', style='dashed') # 设置指定边,虚线
nx.draw_networkx_edge_labels(DG, pos, edge_labels=labels, font_color='dimgrey') # 显示边的权值
nx.draw_networkx_edges(DG, pos, edgelist=cpDG.edges, edge_color='r', width=2) # 设置指定边的颜: 显示关键路径
ax.set_title("Project network graph by youcans@xupt")
ax.text(16, 0, "youcans-xupt", color='gainsboro')
plt.xlim(-2, 22)
plt.ylim(-1, 9)
plt.axis('on')
plt.show() # YouCans, XUPT
4.5 程序运行结果
顶点(事件)的最早时间 VE, 最晚时间 VL:
事件 1: VE= 0 VL= 0
事件 2: VE= 5 VL= 6
事件 3: VE= 10 VL= 10
事件 4: VE= 14 VL= 16
事件 5: VE= 10 VL= 10
事件 6: VE= 31 VL= 31
事件 7: VE= 35 VL= 36
事件 8: VE= 51 VL= 51
边(活动)的最早开始时间 ES, 最晚开始时间 LS:
作业 (1, 2): ES= 0 LS= 1 DU= 5
作业 (1, 3): ES= 0 LS= 0 DU= 10
作业 (1, 4): ES= 0 LS= 5 DU= 11
作业 (2, 5): ES= 5 LS= 6 DU= 4
作业 (3, 4): ES= 10 LS= 12 DU= 4
作业 (3, 5): ES= 10 LS= 10 DU= 0
作业 (4, 6): ES= 14 LS= 16 DU= 15
作业 (5, 6): ES= 10 LS= 10 DU= 21
作业 (5, 7): ES= 10 LS= 11 DU= 25
作业 (5, 8): ES= 10 LS= 16 DU= 35
作业 (6, 7): ES= 31 LS= 36 DU= 0
作业 (6, 8): ES= 31 LS= 31 DU= 20
作业 (7, 8): ES= 35 LS= 36 DU= 15
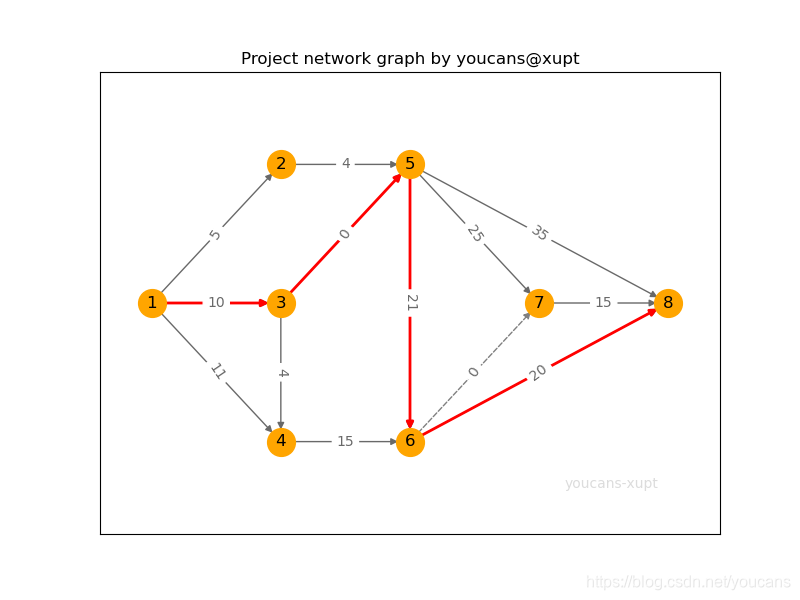
关键路径:[(1, 3), (3, 5), (5, 6), (6, 8)]
项目最短工期:51
【本节完】
版权声明:
欢迎关注『Python小白的数学建模课 @ Youcans』 原创作品
原创作品,转载必须标注原文链接:(https://blog.csdn.net/youcans/article/details/118754623)。
Copyright 2021 Youcans, XUPT
Crated:2021-07-26
欢迎关注 『Python小白的数学建模课 @ Youcans』 系列,持续更新
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python小白的数学建模课-04.整数规划
Python小白的数学建模课-05.0-1规划
Python小白的数学建模课-06.固定费用问题
Python小白的数学建模课-07.选址问题
Python小白的数学建模课-09.微分方程模型
Python小白的数学建模课-10.微分方程边值问题
Python小白的数学建模课-12.非线性规划
Python小白的数学建模课-15.图论的基本概念
Python小白的数学建模课-16.最短路径算法
Python小白的数学建模课-17.条件最短路径算法
Python小白的数学建模课-18.最小生成树问题
Python小白的数学建模课-19.网络流优化问题
Python小白的数学建模课-20.网络流优化案例
Python小白的数学建模课-21.关键路径法
Python小白的数学建模课-A1.国赛赛题类型分析
Python小白的数学建模课-A2.2021年数维杯C题探讨
Python小白的数学建模课-A3.12个新冠疫情数模竞赛赛题及短评
Python小白的数学建模课-B2. 新冠疫情 SI模型
Python小白的数学建模课-B3. 新冠疫情 SIS模型
Python小白的数学建模课-B4. 新冠疫情 SIR模型
Python小白的数学建模课-B5. 新冠疫情 SEIR模型
Python小白的数学建模课-B6. 新冠疫情 SEIR改进模型
Python数模笔记-PuLP库
Python数模笔记-StatsModels统计回归
Python数模笔记-Sklearn
Python数模笔记-NetworkX
Python数模笔记-模拟退火算法