学习目标

1.希尔排序
2.计数排序
3.桶排序
4.基数排序

学习前奏

希尔排序

希尔排序(Shell Sort)是一种分组插入排序算法。
首先取一个整数d,=n/2，将元素分为d个组，每组相邻
量元素之间距离为d，在各组内进行直接插入排序;
取第二个整数d2=d/2，重复上述分组排序过程，直到
d;=1，即所有元素在同-组内进行直接插入排序。
希尔排序每趟并不使某些元素有序，而是使整体数据越
来越接近有序;最后一趟排序使得所有数据有序。

计数排序

对列表进行排序，已知列表中的数范围都在0到100之间。设
计时间复杂度为O(n)的算法。

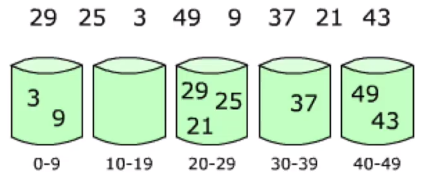
桶排序

在计数排序中，如果元素的范围比较大(比如在倒亿之间)，如何改造算法?
桶排序(Bucket Sort):首先将元素分在不同的桶中，在对每.个桶中的元素排序。
bucket

基数排序

多关键字排序:加入现在有一个员工表，要求按照薪资排序，年龄相同的员工按照年龄排序。
先按照年龄进行排序，再按照薪资进行稳定的排序。
对32,13,94,52,17,54,93排序，是否可以看做多关键字排序?

一：希尔排序

在快速排序的基础上做修改

def insert_sort_gap(li,gap):
	for i in range(gap,len(li)):
		tmp = li[gap]
		j = i - gap
		while j >= 0 and li[j] > tmp:
			li[j+gap] = li[j]
			j -= gap
		li[j+gap] = tmp

def shell_sort(li):
	d = len(li)//2
	while d >= 1:
		insert_sort_gap(li,d)
		d //= 2

li = list(range(1000))
import random
random.shuffle(li)
print(li)

希尔排序的时间复杂度讨论比较复杂，并且和选取的gap序列
有关。可以去看看这个网站对它时间复杂度的说明。
在这里插入图片描述

二：计数排序

def count_sort(li,max_count=100):
	count = [0 for _ in range(max_count+1)]
	for val in li:
		count[val] +=1
	li.clear()
	for ind,val in enumerate(count):
		for i in range(val):
			li.append(ind)

import random
li = [random.randint(0,100) for _ in range(1000)]
print(li)
count_sort(li)
print(li)

三：桶排序

def bucket_sort(li, n=100, max_num=10000):
	buckets = [[] for _ in range(n)] # 创建桶
	for val in li:
		i = min(val // (max_num // n),n-1)  # i表示放到几号桶
		buckets[i].append(val)
		for j in range(len(buckets[i])-1, 0, -1):
			if buckets[i][j] < buckets[i][j-1]:
				buckets[i][j], buckets[i][j-1]=buckets[i][j-1], buckets[i][j]
			else:
				break
		sorted_li = []
		for buc in buckets:
			sorted_li.extend(buc)
		return sorted_li

import random
li = [random.randint(0,1000) for i in range(10000)]
li = bucket_sort(li)
print(li)

四：基数排序

def radix_sort(li):
	max_num = max(li)
	it = 0
	while 10 ** it <= max_num:
		buckets = [[] for _ in range(10)]
		for var in li:
			digit = (var // 10 ** it) % 10
			buckets[digit].append(var)
		li.clear()
		for but in buckets:
			li.extend(buc)
		it += 1

import random
li = list(range(1000))
random.shuffle(li)
radix_sort(li)
print(li)