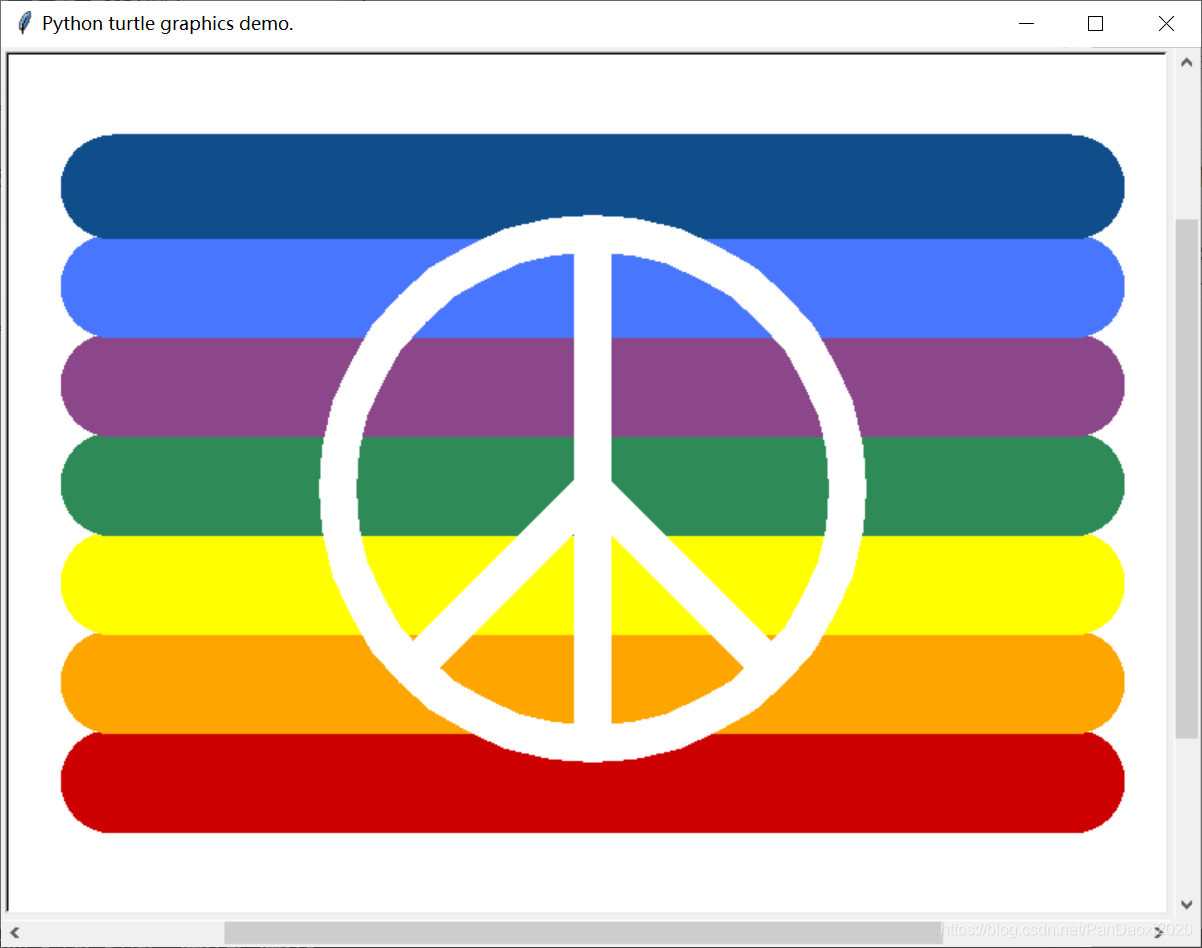
①绘制彩虹图案:
#!/usr/bin/env python3
""" turtle-example-suite:
tdemo_peace.py
A simple drawing suitable as a beginner's
programming example. Aside from the
peacecolors assignment and the for loop,
it only uses turtle commands.
"""
from turtle import *
def main():
peacecolors = ("red3", "orange", "yellow",
"seagreen4", "orchid4",
"royalblue1", "dodgerblue4")
reset()
Screen()
up()
goto(-320,-195)
width(70)
for pcolor in peacecolors:
color(pcolor)
down()
forward(640)
up()
backward(640)
left(90)
forward(66)
right(90)
width(25)
color("white")
goto(0,-170)
down()
circle(170)
left(90)
forward(340)
up()
left(180)
forward(170)
right(45)
down()
forward(170)
up()
backward(170)
left(90)
down()
forward(170)
up()
goto(0,300) # vanish if hideturtle() is not available ;-)
return "Done!"
if __name__ == "__main__":
main()
mainloop()
②五等分(密集恐惧症者勿入):

#!/usr/bin/env python3
""" xturtle-example-suite:
xtx_kites_and_darts.py
Constructs two aperiodic penrose-tilings,
consisting of kites and darts, by the method
of inflation in six steps.
Starting points are the patterns "sun"
consisting of five kites and "star"
consisting of five darts.
For more information see:
http://en.wikipedia.org/wiki/Penrose_tiling
-------------------------------------------
"""
from turtle import *
from math import cos, pi
from time import clock, sleep
f = (5**0.5-1)/2.0 # (sqrt(5)-1)/2 -- golden ratio
d = 2 * cos(3*pi/10)
def kite(l):
fl = f * l
lt(36)
fd(l)
rt(108)
fd(fl)
rt(36)
fd(fl)
rt(108)
fd(l)
rt(144)
def dart(l):
fl = f * l
lt(36)
fd(l)
rt(144)
fd(fl)
lt(36)
fd(fl)
rt(144)
fd(l)
rt(144)
def inflatekite(l, n):
if n == 0:
px, py = pos()
h, x, y = int(heading()), round(px,3), round(py,3)
tiledict[(h,x,y)] = True
return
fl = f * l
lt(36)
inflatedart(fl, n-1)
fd(l)
rt(144)
inflatekite(fl, n-1)
lt(18)
fd(l*d)
rt(162)
inflatekite(fl, n-1)
lt(36)
fd(l)
rt(180)
inflatedart(fl, n-1)
lt(36)
def inflatedart(l, n):
if n == 0:
px, py = pos()
h, x, y = int(heading()), round(px,3), round(py,3)
tiledict[(h,x,y)] = False
return
fl = f * l
inflatekite(fl, n-1)
lt(36)
fd(l)
rt(180)
inflatedart(fl, n-1)
lt(54)
fd(l*d)
rt(126)
inflatedart(fl, n-1)
fd(l)
rt(144)
def draw(l, n, th=2):
clear()
l = l * f**n
shapesize(l/100.0, l/100.0, th)
for k in tiledict:
h, x, y = k
setpos(x, y)
setheading(h)
if tiledict[k]:
shape("kite")
color("black", (0, 0.75, 0))
else:
shape("dart")
color("black", (0.75, 0, 0))
stamp()
def sun(l, n):
for i in range(5):
inflatekite(l, n)
lt(72)
def star(l,n):
for i in range(5):
inflatedart(l, n)
lt(72)
def makeshapes():
tracer(0)
begin_poly()
kite(100)
end_poly()
register_shape("kite", get_poly())
begin_poly()
dart(100)
end_poly()
register_shape("dart", get_poly())
tracer(1)
def start():
reset()
ht()
pu()
makeshapes()
resizemode("user")
def test(l=200, n=4, fun=sun, startpos=(0,0), th=2):
global tiledict
goto(startpos)
setheading(0)
tiledict = {}
a = clock()
tracer(0)
fun(l, n)
b = clock()
draw(l, n, th)
tracer(1)
c = clock()
print("Calculation: %7.4f s" % (b - a))
print("Drawing: %7.4f s" % (c - b))
print("Together: %7.4f s" % (c - a))
nk = len([x for x in tiledict if tiledict[x]])
nd = len([x for x in tiledict if not tiledict[x]])
print("%d kites and %d darts = %d pieces." % (nk, nd, nk+nd))
def demo(fun=sun):
start()
for i in range(8):
a = clock()
test(300, i, fun)
b = clock()
t = b - a
if t < 2:
sleep(2 - t)
def main():
#title("Penrose-tiling with kites and darts.")
mode("logo")
bgcolor(0.3, 0.3, 0)
demo(sun)
sleep(2)
demo(star)
pencolor("black")
goto(0,-200)
pencolor(0.7,0.7,1)
write("Please wait...",
align="center", font=('Arial Black', 36, 'bold'))
test(600, 8, startpos=(70, 117))
return "Done"
if __name__ == "__main__":
msg = main()
mainloop()
③旋转绘制:
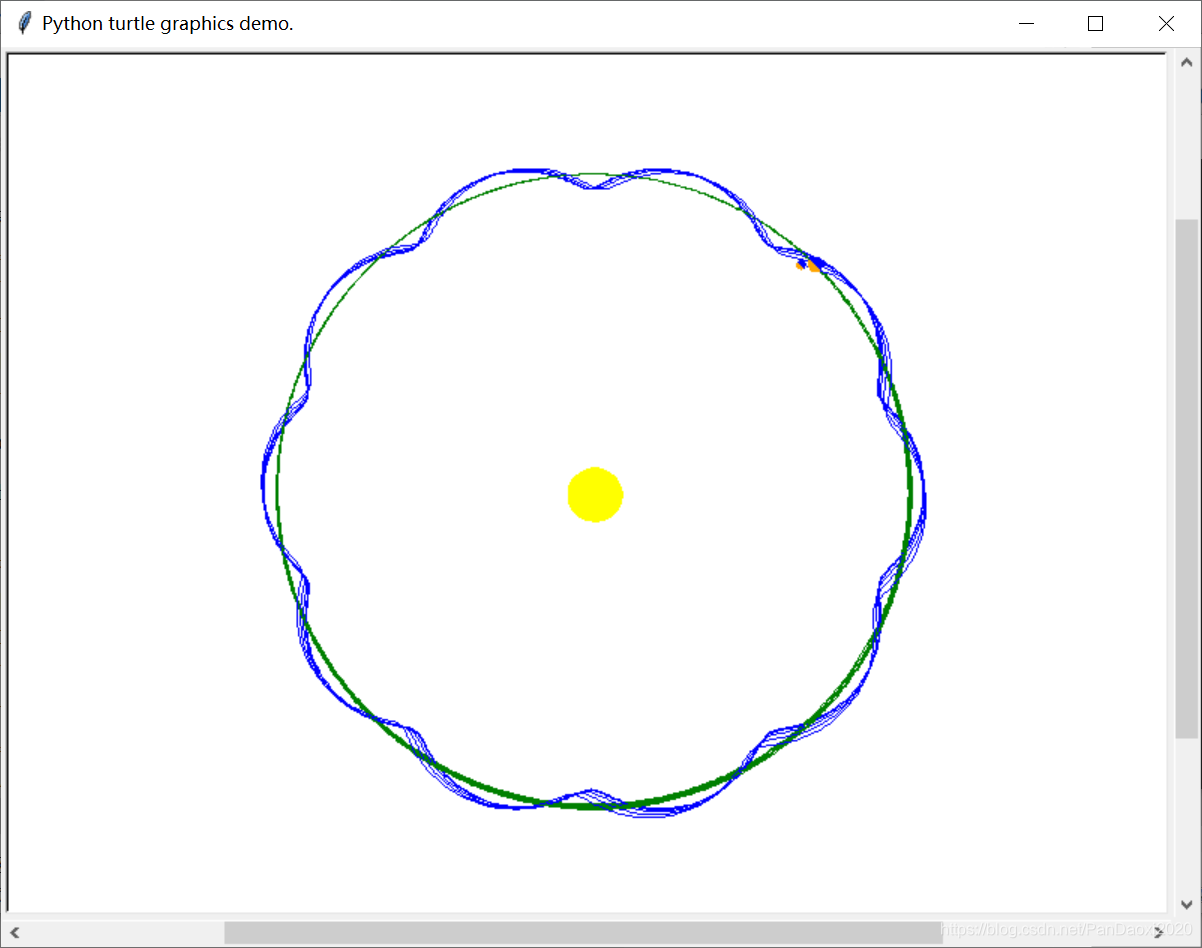
#!/usr/bin/env python3
""" turtle-example-suite:
tdemo_planets_and_moon.py
Gravitational system simulation using the
approximation method from Feynman-lectures,
p.9-8, using turtlegraphics.
Example: heavy central body, light planet,
very light moon!
Planet has a circular orbit, moon a stable
orbit around the planet.
You can hold the movement temporarily by
pressing the left mouse button with the
mouse over the scrollbar of the canvas.
"""
from turtle import Shape, Turtle, mainloop, Vec2D as Vec
G = 8
class GravSys(object):
def __init__(self):
self.planets = []
self.t = 0
self.dt = 0.01
def init(self):
for p in self.planets:
p.init()
def start(self):
for i in range(10000):
self.t += self.dt
for p in self.planets:
p.step()
class Star(Turtle):
def __init__(self, m, x, v, gravSys, shape):
Turtle.__init__(self, shape=shape)
self.penup()
self.m = m
self.setpos(x)
self.v = v
gravSys.planets.append(self)
self.gravSys = gravSys
self.resizemode("user")
self.pendown()
def init(self):
dt = self.gravSys.dt
self.a = self.acc()
self.v = self.v + 0.5*dt*self.a
def acc(self):
a = Vec(0,0)
for planet in self.gravSys.planets:
if planet != self:
v = planet.pos()-self.pos()
a += (G*planet.m/abs(v)**3)*v
return a
def step(self):
dt = self.gravSys.dt
self.setpos(self.pos() + dt*self.v)
if self.gravSys.planets.index(self) != 0:
self.setheading(self.towards(self.gravSys.planets[0]))
self.a = self.acc()
self.v = self.v + dt*self.a
## create compound yellow/blue turtleshape for planets
def main():
s = Turtle()
s.reset()
s.getscreen().tracer(0,0)
s.ht()
s.pu()
s.fd(6)
s.lt(90)
s.begin_poly()
s.circle(6, 180)
s.end_poly()
m1 = s.get_poly()
s.begin_poly()
s.circle(6,180)
s.end_poly()
m2 = s.get_poly()
planetshape = Shape("compound")
planetshape.addcomponent(m1,"orange")
planetshape.addcomponent(m2,"blue")
s.getscreen().register_shape("planet", planetshape)
s.getscreen().tracer(1,0)
## setup gravitational system
gs = GravSys()
sun = Star(1000000, Vec(0,0), Vec(0,-2.5), gs, "circle")
sun.color("yellow")
sun.shapesize(1.8)
sun.pu()
earth = Star(12500, Vec(210,0), Vec(0,195), gs, "planet")
earth.pencolor("green")
earth.shapesize(0.8)
moon = Star(1, Vec(220,0), Vec(0,295), gs, "planet")
moon.pencolor("blue")
moon.shapesize(0.5)
gs.init()
gs.start()
return "Done!"
if __name__ == '__main__':
main()
mainloop()
④旋转的舞蹈(密集恐惧症者勿入):
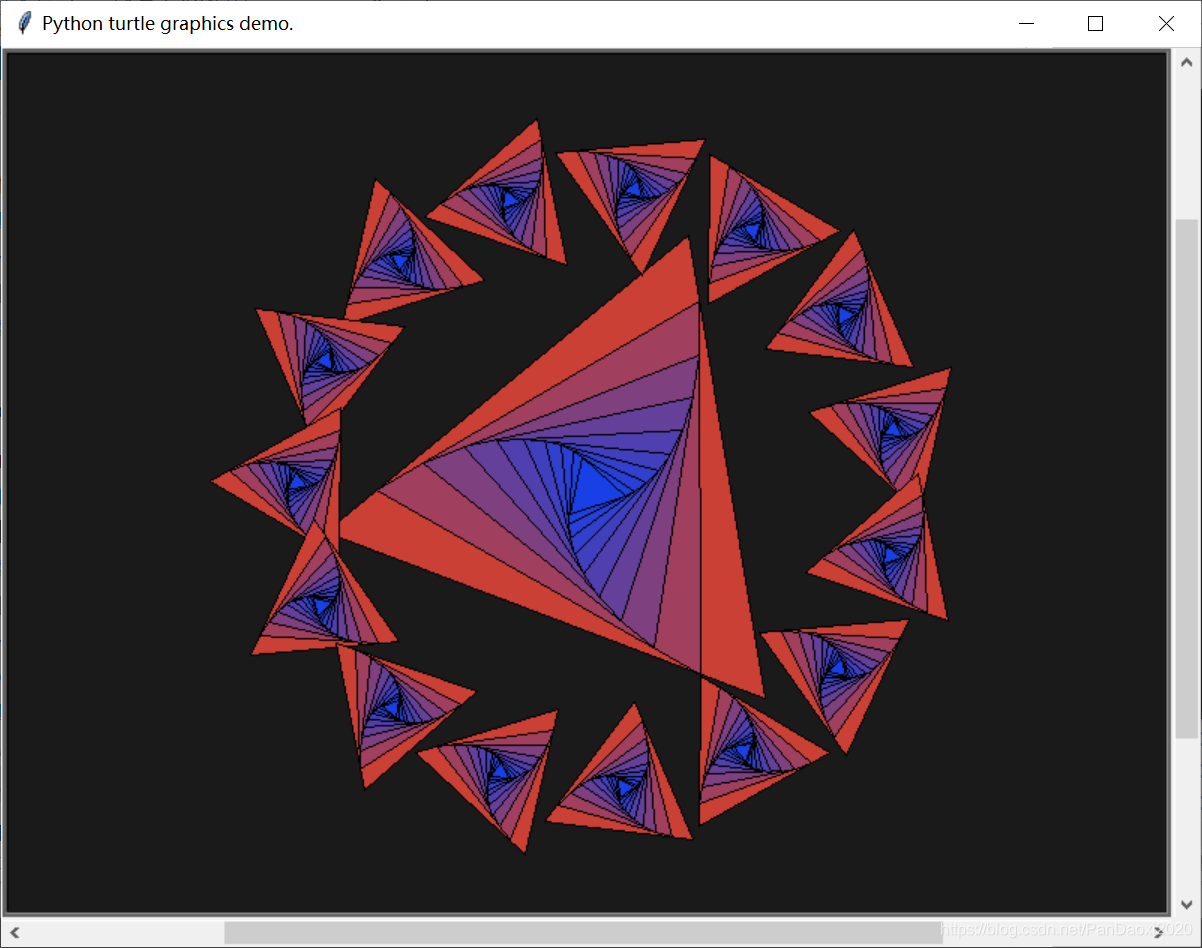
""" turtle-example-suite:
tdemo_round_dance.py
(Needs version 1.1 of the turtle module that
comes with Python 3.1)
Dancing turtles have a compound shape
consisting of a series of triangles of
decreasing size.
Turtles march along a circle while rotating
pairwise in opposite direction, with one
exception. Does that breaking of symmetry
enhance the attractiveness of the example?
Press any key to stop the animation.
Technically: demonstrates use of compound
shapes, transformation of shapes as well as
cloning turtles. The animation is
controlled through update().
"""
from turtle import *
def stop():
global running
running = False
def main():
global running
clearscreen()
bgcolor("gray10")
tracer(False)
shape("triangle")
f = 0.793402
phi = 9.064678
s = 5
c = 1
# create compound shape
sh = Shape("compound")
for i in range(10):
shapesize(s)
p =get_shapepoly()
s *= f
c *= f
tilt(-phi)
sh.addcomponent(p, (c, 0.25, 1-c), "black")
register_shape("multitri", sh)
# create dancers
shapesize(1)
shape("multitri")
pu()
setpos(0, -200)
dancers = []
for i in range(180):
fd(7)
tilt(-4)
lt(2)
update()
if i % 12 == 0:
dancers.append(clone())
home()
# dance
running = True
onkeypress(stop)
listen()
cs = 1
while running:
ta = -4
for dancer in dancers:
dancer.fd(7)
dancer.lt(2)
dancer.tilt(ta)
ta = -4 if ta > 0 else 2
if cs < 180:
right(4)
shapesize(cs)
cs *= 1.005
update()
return "DONE!"
if __name__=='__main__':
print(main())
mainloop()
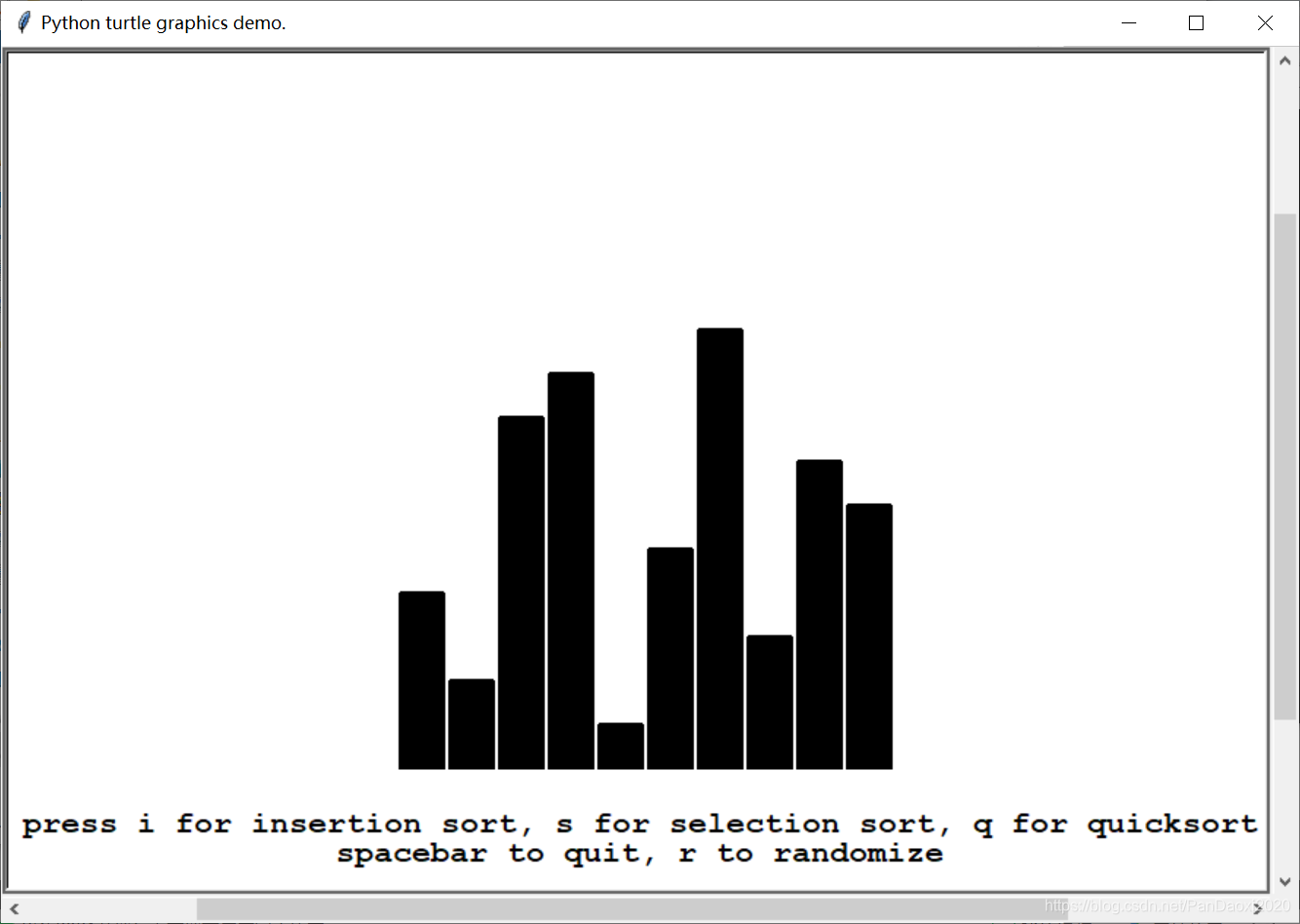
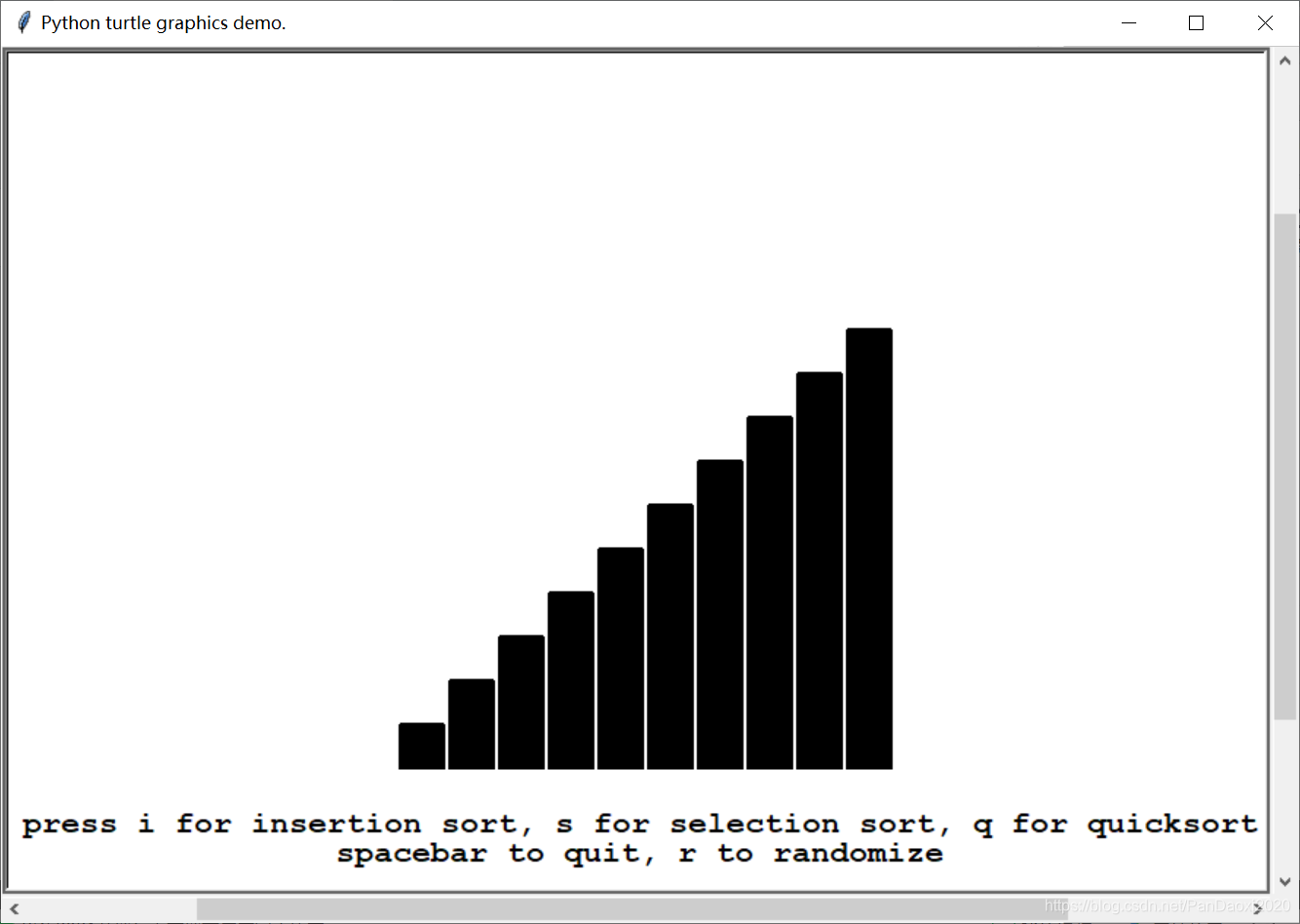
⑤排序:
#!/usr/bin/env python3
"""
sorting_animation.py
A minimal sorting algorithm animation:
Sorts a shelf of 10 blocks using insertion
sort, selection sort and quicksort.
Shelfs are implemented using builtin lists.
Blocks are turtles with shape "square", but
stretched to rectangles by shapesize()
---------------------------------------
To exit press space button
---------------------------------------
"""
from turtle import *
import random
class Block(Turtle):
def __init__(self, size):
self.size = size
Turtle.__init__(self, shape="square", visible=False)
self.pu()
self.shapesize(size * 1.5, 1.5, 2) # square-->rectangle
self.fillcolor("black")
self.st()
def glow(self):
self.fillcolor("red")
def unglow(self):
self.fillcolor("black")
def __repr__(self):
return "Block size: {0}".format(self.size)
class Shelf(list):
def __init__(self, y):
"create a shelf. y is y-position of first block"
self.y = y
self.x = -150
def push(self, d):
width, _, _ = d.shapesize()
# align blocks by the bottom edge
y_offset = width / 2 * 20
d.sety(self.y + y_offset)
d.setx(self.x + 34 * len(self))
self.append(d)
def _close_gap_from_i(self, i):
for b in self[i:]:
xpos, _ = b.pos()
b.setx(xpos - 34)
def _open_gap_from_i(self, i):
for b in self[i:]:
xpos, _ = b.pos()
b.setx(xpos + 34)
def pop(self, key):
b = list.pop(self, key)
b.glow()
b.sety(200)
self._close_gap_from_i(key)
return b
def insert(self, key, b):
self._open_gap_from_i(key)
list.insert(self, key, b)
b.setx(self.x + 34 * key)
width, _, _ = b.shapesize()
# align blocks by the bottom edge
y_offset = width / 2 * 20
b.sety(self.y + y_offset)
b.unglow()
def isort(shelf):
length = len(shelf)
for i in range(1, length):
hole = i
while hole > 0 and shelf[i].size < shelf[hole - 1].size:
hole = hole - 1
shelf.insert(hole, shelf.pop(i))
return
def ssort(shelf):
length = len(shelf)
for j in range(0, length - 1):
imin = j
for i in range(j + 1, length):
if shelf[i].size < shelf[imin].size:
imin = i
if imin != j:
shelf.insert(j, shelf.pop(imin))
def partition(shelf, left, right, pivot_index):
pivot = shelf[pivot_index]
shelf.insert(right, shelf.pop(pivot_index))
store_index = left
for i in range(left, right): # range is non-inclusive of ending value
if shelf[i].size < pivot.size:
shelf.insert(store_index, shelf.pop(i))
store_index = store_index + 1
shelf.insert(store_index, shelf.pop(right)) # move pivot to correct position
return store_index
def qsort(shelf, left, right):
if left < right:
pivot_index = left
pivot_new_index = partition(shelf, left, right, pivot_index)
qsort(shelf, left, pivot_new_index - 1)
qsort(shelf, pivot_new_index + 1, right)
def randomize():
disable_keys()
clear()
target = list(range(10))
random.shuffle(target)
for i, t in enumerate(target):
for j in range(i, len(s)):
if s[j].size == t + 1:
s.insert(i, s.pop(j))
show_text(instructions1)
show_text(instructions2, line=1)
enable_keys()
def show_text(text, line=0):
line = 20 * line
goto(0,-250 - line)
write(text, align="center", font=("Courier", 16, "bold"))
def start_ssort():
disable_keys()
clear()
show_text("Selection Sort")
ssort(s)
clear()
show_text(instructions1)
show_text(instructions2, line=1)
enable_keys()
def start_isort():
disable_keys()
clear()
show_text("Insertion Sort")
isort(s)
clear()
show_text(instructions1)
show_text(instructions2, line=1)
enable_keys()
def start_qsort():
disable_keys()
clear()
show_text("Quicksort")
qsort(s, 0, len(s) - 1)
clear()
show_text(instructions1)
show_text(instructions2, line=1)
enable_keys()
def init_shelf():
global s
s = Shelf(-200)
vals = (4, 2, 8, 9, 1, 5, 10, 3, 7, 6)
for i in vals:
s.push(Block(i))
def disable_keys():
onkey(None, "s")
onkey(None, "i")
onkey(None, "q")
onkey(None, "r")
def enable_keys():
onkey(start_isort, "i")
onkey(start_ssort, "s")
onkey(start_qsort, "q")
onkey(randomize, "r")
onkey(bye, "space")
def main():
getscreen().clearscreen()
ht(); penup()
init_shelf()
show_text(instructions1)
show_text(instructions2, line=1)
enable_keys()
listen()
return "EVENTLOOP"
instructions1 = "press i for insertion sort, s for selection sort, q for quicksort"
instructions2 = "spacebar to quit, r to randomize"
if __name__=="__main__":
msg = main()
mainloop()
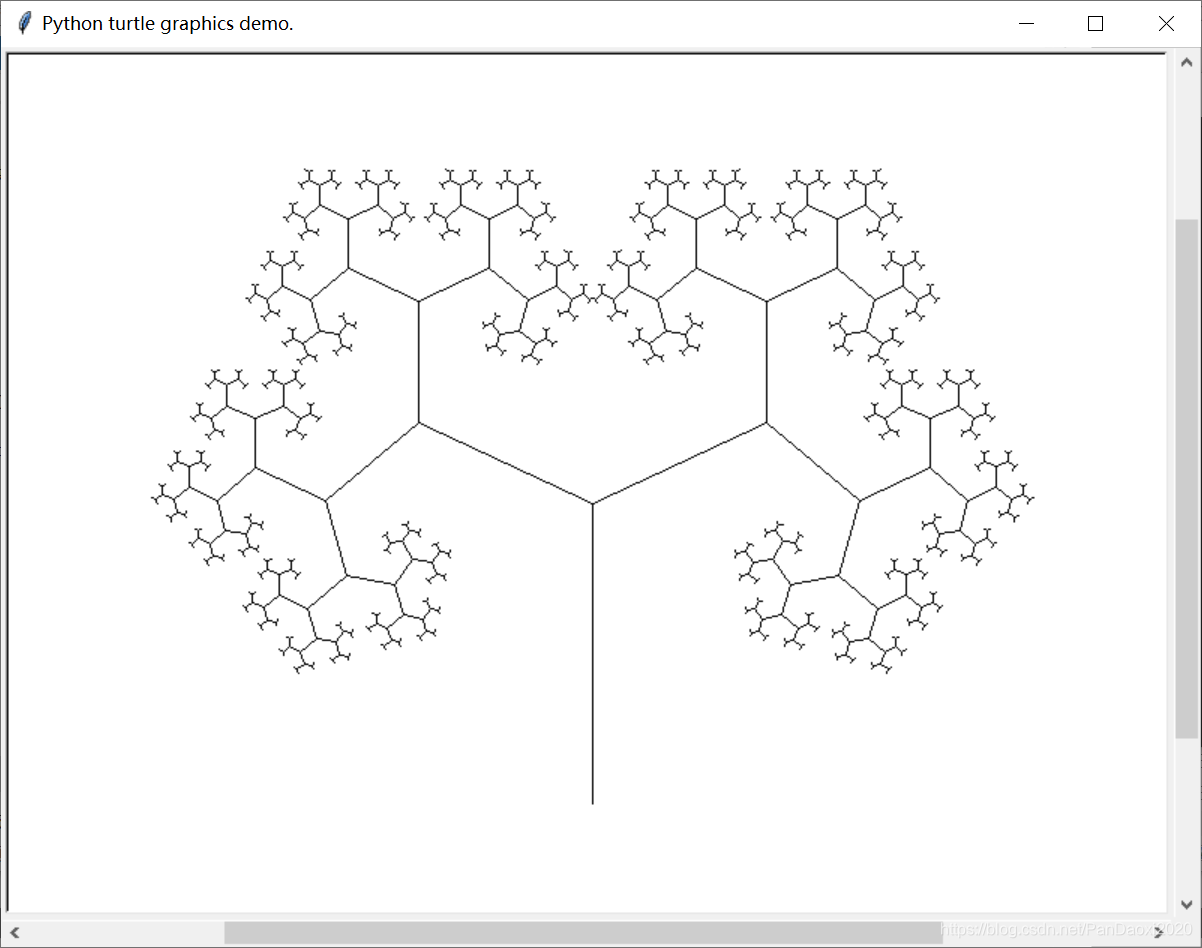
⑥绘制海龟树(深度优先算法):
#!/usr/bin/env python3
""" turtle-example-suite:
tdemo_tree.py
Displays a 'breadth-first-tree' - in contrast
to the classical Logo tree drawing programs,
which use a depth-first-algorithm.
Uses:
(1) a tree-generator, where the drawing is
quasi the side-effect, whereas the generator
always yields None.
(2) Turtle-cloning: At each branching point
the current pen is cloned. So in the end
there are 1024 turtles.
"""
from turtle import Turtle, mainloop
from time import clock
def tree(plist, l, a, f):
""" plist is list of pens
l is length of branch
a is half of the angle between 2 branches
f is factor by which branch is shortened
from level to level."""
if l > 3:
lst = []
for p in plist:
p.forward(l)
q = p.clone()
p.left(a)
q.right(a)
lst.append(p)
lst.append(q)
for x in tree(lst, l*f, a, f):
yield None
def maketree():
p = Turtle()
p.setundobuffer(None)
p.hideturtle()
p.speed(0)
p.getscreen().tracer(30,0)
p.left(90)
p.penup()
p.forward(-210)
p.pendown()
t = tree([p], 200, 65, 0.6375)
for x in t:
pass
print(len(p.getscreen().turtles()))
def main():
a=clock()
maketree()
b=clock()
return "done: %.2f sec." % (b-a)
if __name__ == "__main__":
msg = main()
print(msg)
mainloop()
⑦两个画笔:
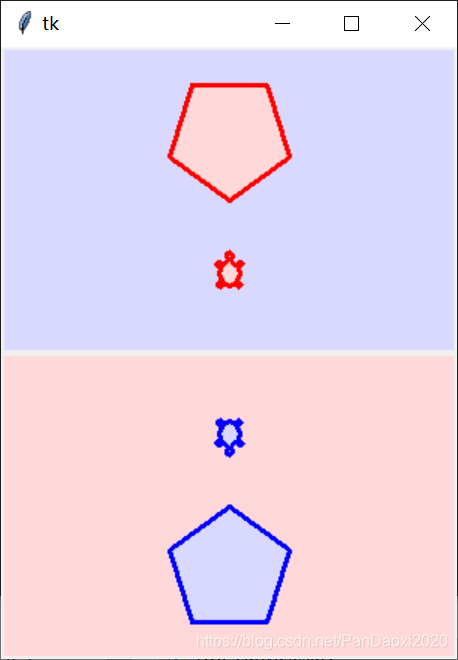
"""turtledemo.two_canvases
Use TurtleScreen and RawTurtle to draw on two
distinct canvases in a separate windows. The
new window must be separately closed in
addition to pressing the STOP button.
"""
from turtle import TurtleScreen, RawTurtle, TK
def main():
root = TK.Tk()
cv1 = TK.Canvas(root, width=300, height=200, bg="#ddffff")
cv2 = TK.Canvas(root, width=300, height=200, bg="#ffeeee")
cv1.pack()
cv2.pack()
s1 = TurtleScreen(cv1)
s1.bgcolor(0.85, 0.85, 1)
s2 = TurtleScreen(cv2)
s2.bgcolor(1, 0.85, 0.85)
p = RawTurtle(s1)
q = RawTurtle(s2)
p.color("red", (1, 0.85, 0.85))
p.width(3)
q.color("blue", (0.85, 0.85, 1))
q.width(3)
for t in p,q:
t.shape("turtle")
t.lt(36)
q.lt(180)
for t in p, q:
t.begin_fill()
for i in range(5):
for t in p, q:
t.fd(50)
t.lt(72)
for t in p,q:
t.end_fill()
t.lt(54)
t.pu()
t.bk(50)
return "EVENTLOOP"
if __name__ == '__main__':
main()
TK.mainloop() # keep window open until user closes it
⑧绘制好看的圆形图案:
""" turtle-example-suite:
tdemo_wikipedia3.py
This example is
inspired by the Wikipedia article on turtle
graphics. (See example wikipedia1 for URLs)
First we create (ne-1) (i.e. 35 in this
example) copies of our first turtle p.
Then we let them perform their steps in
parallel.
Followed by a complete undo().
"""
from turtle import Screen, Turtle, mainloop
from time import clock, sleep
def mn_eck(p, ne,sz):
turtlelist = [p]
#create ne-1 additional turtles
for i in range(1,ne):
q = p.clone()
q.rt(360.0/ne)
turtlelist.append(q)
p = q
for i in range(ne):
c = abs(ne/2.0-i)/(ne*.7)
# let those ne turtles make a step
# in parallel:
for t in turtlelist:
t.rt(360./ne)
t.pencolor(1-c,0,c)
t.fd(sz)
def main():
s = Screen()
s.bgcolor("black")
p=Turtle()
p.speed(0)
p.hideturtle()
p.pencolor("red")
p.pensize(3)
s.tracer(36,0)
at = clock()
mn_eck(p, 36, 19)
et = clock()
z1 = et-at
sleep(1)
at = clock()
while any([t.undobufferentries() for t in s.turtles()]):
for t in s.turtles():
t.undo()
et = clock()
return "runtime: %.3f sec" % (z1+et-at)
if __name__ == '__main__':
msg = main()
print(msg)
mainloop()
⑨阴阳图:

#!/usr/bin/env python3
""" turtle-example-suite:
tdemo_yinyang.py
Another drawing suitable as a beginner's
programming example.
The small circles are drawn by the circle
command.
"""
from turtle import *
def yin(radius, color1, color2):
width(3)
color("black", color1)
begin_fill()
circle(radius/2., 180)
circle(radius, 180)
left(180)
circle(-radius/2., 180)
end_fill()
left(90)
up()
forward(radius*0.35)
right(90)
down()
color(color1, color2)
begin_fill()
circle(radius*0.15)
end_fill()
left(90)
up()
backward(radius*0.35)
down()
left(90)
def main():
reset()
yin(200, "black", "white")
yin(200, "white", "black")
ht()
return "Done!"
if __name__ == '__main__':
main()
mainloop()