
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
1 简单练习
输出一个 5 ? 5 5*5 5?5的单位矩阵
A = np.eye(5)
A
array([[1., 0., 0., 0., 0.], [0., 1., 0., 0., 0.], [0., 0., 1., 0., 0.], [0., 0., 0., 1., 0.], [0., 0., 0., 0., 1.]])
2 单变量的线性回归
整个2的部分需要根据城市人口数量,预测开小吃店的利润
数据在ex1data1.txt里,第一列是城市人口数量,第二列是该城市小吃店利润
2.1 Plotting the Data
读入数据,然后展示数据
data = pd.read_csv('ex1data1.txt',names=['population','profit'])# 读取数据并赋予列名
data.head()#看前五行
| population | profit | |
|---|---|---|
| 0 | 6.1101 | 17.5920 |
| 1 | 5.5277 | 9.1302 |
| 2 | 8.5186 | 13.6620 |
| 3 | 7.0032 | 11.8540 |
| 4 | 5.8598 | 6.8233 |
data.describe()
| population | profit | |
|---|---|---|
| count | 97.000000 | 97.000000 |
| mean | 8.159800 | 5.839135 |
| std | 3.869884 | 5.510262 |
| min | 5.026900 | -2.680700 |
| 25% | 5.707700 | 1.986900 |
| 50% | 6.589400 | 4.562300 |
| 75% | 8.578100 | 7.046700 |
| max | 22.203000 | 24.147000 |
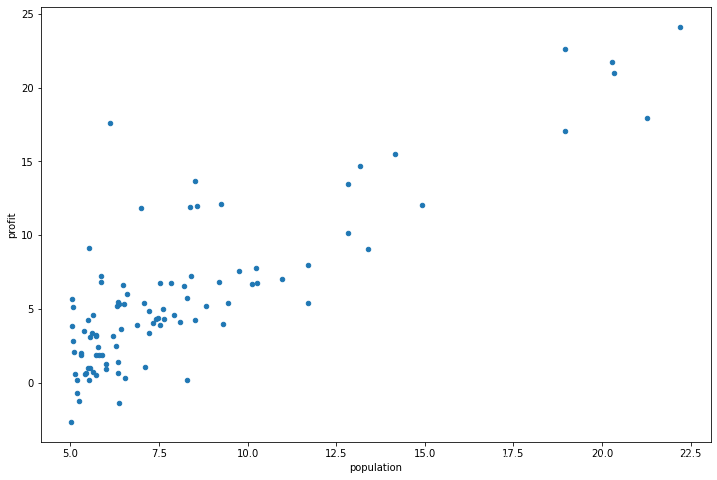
看下原始数据
data.plot(kind='scatter', x='population', y='profit', figsize=(12,8))
plt.show()
2.2 梯度下降
这个部分需要在现有数据集上,训练线性回归的参数θ
2.2.1 公式
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}}
J(θ)=2m1?i=1∑m?(hθ?(x(i))?y(i))2
其中:
h
θ
(
x
)
=
θ
T
X
=
θ
0
x
0
+
θ
1
x
1
+
θ
2
x
2
+
…
+
θ
n
x
n
h_{\theta}(x)=\theta^{T} X=\theta_{0} x_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{n} x_{n}
hθ?(x)=θTX=θ0?x0?+θ1?x1?+θ2?x2?+…+θn?xn?
def computeCost(X,y,theta):
inner = np.power((X*theta.T-y),2)#因为输入样本的矩阵被转置过,所以此处的处理与上述公式稍有不同;matrix的优势就是相对简单的运算符号,比如两个矩阵相乘,就是用符号*
return np.sum(inner)/(2*len(X))
2.2.2实现
数据前面已经读取完毕,我们要为加入一列x,用于更新 θ 0 \theta_0 θ0?,然后我们将 θ \theta θ初始化为0,学习率初始化为0.01,迭代次数为1500次
data.insert(0, 'Ones', 1)
来做一些变量初始化
# 初始化X和y
cols = data.shape[1]
X = data.iloc[:,:-1]#X是data里的除最后列
y = data.iloc[:,cols-1:cols]#y是data最后一列
观察下X(训练集)and y(目标变量)是否正确
X.head()#观察前5行
| Ones | population | |
|---|---|---|
| 0 | 1 | 6.1101 |
| 1 | 1 | 5.5277 |
| 2 | 1 | 8.5186 |
| 3 | 1 | 7.0032 |
| 4 | 1 | 5.8598 |
y.head()
| profit | |
|---|---|
| 0 | 17.5920 |
| 1 | 9.1302 |
| 2 | 13.6620 |
| 3 | 11.8540 |
| 4 | 6.8233 |
代价函数是应该是numpy矩阵,所以需要转换X和Y,然后才能使用它们。 还需要初始化 θ \theta θ。
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))#只需要theta0和theta1,所以为1*2的矩阵
看下维度
X.shape, theta.shape, y.shape
((97, 2), (1, 2), (97, 1))
computeCost(X,y,theta)
32.072733877455676
2.2.4 梯度下降
θ j : = θ j ? α ? ? θ j J ( θ ) {{\theta }_{j}}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( \theta \right) θj?:=θj??α?θj???J(θ)
def gradientDescent(X, y, theta, alpha, iters):
temp = np.matrix(np.zeros(theta.shape))#构建零值矩阵
parameters = int(theta.ravel().shape[1])#ravel计算需要求解的参数个数,功能:将多维数组降至一维
cost = np.zeros(iters)#构建iters个0的数组
for i in range(iters):
error = (X * theta.T) - y
for j in range(parameters):
term = np.multiply(error, X[:,j])
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
theta = temp
cost[i] = computeCost(X, y, theta)
return theta, cost
#这个部分实现了?的更新
初始化一些附加变量 - 学习速率 α \alpha α和要执行的迭代次数。
alpha = 0.01
iters = 1500
运行梯度下降算法来将我们的参数 θ \theta θ适合于训练集。
g, cost = gradientDescent(X, y, theta, alpha, iters)
g
matrix([[-3.63029144, 1.16636235]])
使用拟合的参数计算训练模型的代价函数(误差)。
computeCost(X,y,g)
4.483388256587726
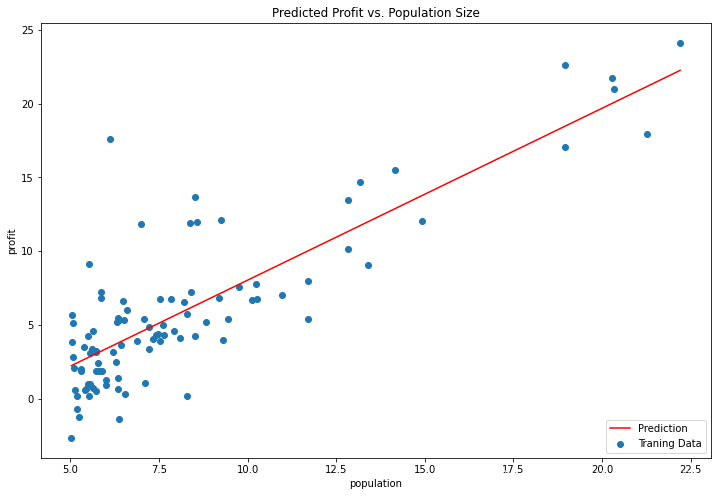
现在来绘制线性模型以及数据,直观地看出它的拟合。fig代表整个图像,ax代表实例
x = np.linspace(data.population.min(), data.population.max(), 100) # 横坐标
f = g[0, 0] + (g[0, 1] * x) # 纵坐标,利润 g[0, 0]代表theta0,g[0, 1]代表theta1
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data['population'], data.profit, label='Traning Data')
ax.legend(loc=4) # 显示标签位置
ax.set_xlabel('population')
ax.set_ylabel('profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
代价数据可视化
fig, ax = plt.subplots(figsize=(8,4))
ax.plot(np.arange(iters), cost, 'r') # np.arange()返回等差数组
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

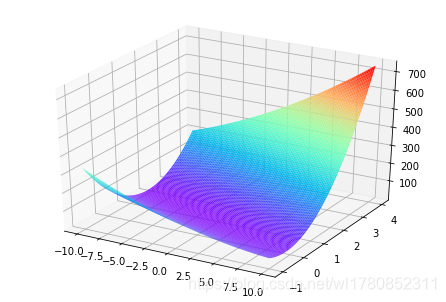
2.2.5 可视化 J ( θ ) J(\theta) J(θ)
为了更好的理解代价函数
J
(
θ
)
J(\theta)
J(θ) , 我们可以将
θ
0
\theta_0
θ0?
和
θ
1
\theta_1
θ1? 的值绘制在二维的网格上。
# 绘制三维的图像
fig = plt.figure()
axes3d = Axes3D(fig)
# 指定参数的区间
theta0_vals = np.linspace(-10, 10, 100)
theta1_vals = np.linspace(-1, 4, 100)
# 存储代价函数值的变量初始化
J_vals = np.zeros((len(theta0_vals), len(theta1_vals)))
# 为代价函数的变量赋值
for i in range(0,len(theta0_vals)):
for j in range(0,len(theta1_vals)):
t = np.zeros((2,1))
t[0] = theta0_vals[j]
t[1] = theta1_vals[i]
t=t.T
J_vals[i,j] = computeCost(X, y, t)
# 下面这句代码不可少
theta0_vals, theta1_vals = np.meshgrid(theta0_vals, theta1_vals) #必须加上这段代码
axes3d.plot_surface(theta0_vals,theta1_vals,J_vals, rstride=1, cstride=1, cmap='rainbow')
plt.show()
3 多变量线性回归
ex1data2.txt里的数据,第一列是房屋大小,第二列是卧室数量,第三列是房屋售价
根据已有数据,建立模型,预测房屋的售价
data2 = pd.read_csv('ex1data2.txt', header=None, names=['Size', 'Bedrooms', 'Price'])
data2.head()
| Size | Bedrooms | Price | |
|---|---|---|---|
| 0 | 2104 | 3 | 399900 |
| 1 | 1600 | 3 | 329900 |
| 2 | 2400 | 3 | 369000 |
| 3 | 1416 | 2 | 232000 |
| 4 | 3000 | 4 | 539900 |
3.1 特征归一化
观察数据发现,size变量是bedrooms变量的1000倍大小,统一量级会让梯度下降收敛的更快。做法就是,将每类特征减去他的平均值后除以标准差
data2 = (data2 - data2.mean()) / data2.std()
data2.head()
| Size | Bedrooms | Price | |
|---|---|---|---|
| 0 | 0.130010 | -0.223675 | 0.475747 |
| 1 | -0.504190 | -0.223675 | -0.084074 |
| 2 | 0.502476 | -0.223675 | 0.228626 |
| 3 | -0.735723 | -1.537767 | -0.867025 |
| 4 | 1.257476 | 1.090417 | 1.595389 |
3.2梯度下降
# 加一列常数项
data2.insert(0, 'Ones', 1)
# 初始化X和y
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]
# 转换成matrix格式,初始化theta
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))
# 运行梯度下降算法
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
computeCost(X2,y2,g2)
0.13068670606095903
3.3正规方程
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:
?
?
θ
j
J
(
θ
j
)
=
0
\frac{\partial }{\partial {{\theta }_{j}}}J\left( {{\theta }_{j}} \right)=0
?θj???J(θj?)=0 。
假设我们的训练集特征矩阵为 X(包含了
x
0
=
1
{{x}_{0}}=1
x0?=1)并且我们的训练集结果为向量 y,则利用正规方程解出向量
θ
=
(
X
T
X
)
?
1
X
T
y
\theta ={{\left( {{X}^{T}}X \right)}^{-1}}{{X}^{T}}y
θ=(XTX)?1XTy 。
上标T代表矩阵转置,上标-1 代表矩阵的逆。设矩阵
A
=
X
T
X
A={{X}^{T}}X
A=XTX,则:
(
X
T
X
)
?
1
=
A
?
1
{{\left( {{X}^{T}}X \right)}^{-1}}={{A}^{-1}}
(XTX)?1=A?1
梯度下降与正规方程的比较:
梯度下降:需要选择学习率α,需要多次迭代,当特征数量n大时也能较好适用,适用于各种类型的模型
正规方程:不需要选择学习率α,一次计算得出,需要计算 ( X T X ) ? 1 {{\left( {{X}^{T}}X \right)}^{-1}} (XTX)?1,如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为 O ( n 3 ) O(n3) O(n3),通常来说当n小于10000 时还是可以接受的,只适用于线性模型,不适合逻辑回归模型等其他模型
# 正规方程
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y#X.T@X等价于X.T.dot(X)
return theta
final_theta2=normalEqn(X, y)#这里用的是data1的数据
final_theta2
matrix([[-3.89578088], [ 1.19303364]])