最近总结路径规划的方法,其中被Dijkstra, SPFA, 优先队列,BFS方法整蒙,有以下几点:
- SPFA即可以用deque实现(朴素),也可以用heapq实现
- Dijkstra即可以用deque实现(朴素),也可以用heapq实现
- heapq实现的SPFA/Dijkstra,跟优先队列的方法有区别吗?
- BFS不就是朴素的Dijkstra吗?
- while循环中什么时候可以return,什么时候不能return
其中总结方法最棘手的是求存在某种限制条件下的最小值,即规定时间内达到终点的最小花费和K站中转内最便宜的航班两题.前者使用SPFA求解,时间最短,而后者使用SPFA却不能通过所有案例!!! -_-
规定时间内达到终点的最小花费
# heap + Dijkstra (SPFA), 时间最快!!!
class Solution:
def minCost(self, maxTime, edges, passingFees):
n = len(passingFees)
g = collections.defaultdict(list)
for u, v, t in edges:
g[u].append((v, t))
g[v].append((u, t))
times = [0] + [float('inf')] * (n - 1)
q = [(passingFees[0], 0, 0)] # cost, time, node
while q:
cost, time, node = heapq.heappop(q)
if node == n - 1: return cost
for neighbor, t in g[node]:
if time + t < times[neighbor] and time + t <= maxTime:
times[neighbor] = time + t
heapq.heappush(q, (cost + passingFees[neighbor], time + t, neighbor))
return -1
很奇怪,该代码如果使用deque实现SPFA的话,并不能完全通过(65/92)!!!
(可能是鄙人实现有误吧,代码如下,希望有大佬看到能够指导我一下)
from collections import deque
class Solution:
def minCost(self, maxTime, edges, passingFees):
n = len(passingFees)
g = collections.defaultdict(list)
for u, v, t in edges:
g[u].append((v, t))
g[v].append((u, t))
times = [0] + [float('inf')] * (n - 1)
q = deque([(passingFees[0], 0, 0)]) # cost, time, node
res = []
while q:
cost, time, node = q.popleft()
if node == n - 1:
res.append(cost)
continue
for neighbor, t in g[node]:
if neighbor not in q:
if time + t < times[neighbor] and time + t <= maxTime:
times[neighbor] = time + t
q.append((cost + passingFees[neighbor], time + t, neighbor))
return -1 if not res else min(res)
K站中转内最便宜的航班
这里采用SPFA代码如下:
from collections import defaultdict
from heapq import *
class Solution(object):
def findCheapestPrice(self, n, flights, src, dst, k):
grids = defaultdict(list)
for u, v, w in flights:
grids[u].append((v, w))
costs = [float('inf')] * n
costs[src] = 0
q = [(0, 0, src)]
while q:
c, num, cur = heappop(q)
for nex, x in grids[cur]:
if costs[nex] > x + c and num + 1 <= k + 1:
costs[nex] = x + c
heappush(q, (x + c, num + 1, nex))
return -1 if costs[dst] == float('inf') else costs[dst]
该方法没有通过所有案列!!!原因在于不能if costs[nex] > x + c,因为可能达到中间某个点是较长路径,此时没有将该情况加入heap中,但最后这条路径却是最优的路径!
注意此题与上一题题的区别,一个是节点值,一个是边权值!!!所以本题不能进行if costs[nex] > x + c判断.其实这两题是相反的,一个是边权一定范围内,取最小节点值(1928);一个是节点数/边数一定范围内,取最小边权值(本题)
此题最优的方法采用的是贝尔曼-福特Bellman-Ford算法
# 贝尔曼-福特Bellman-Ford算法
# https://www.jianshu.com/p/b876fe9b2338
class Solution(object):
def findCheapestPrice(self, n, flights, src, dst, k):
dist = [float('inf')] * n # dist[v]表示到达v的最小花费
dist[src] = 0
for i in range(k + 1): # 对每条边做 k+1 次松弛操作,每次松弛操作实际上是对相邻节点的访问,所以总的中转为k次
dist_old = [_ for _ in dist]
for u, v, w in flights:
dist[v] = min(dist[v], dist_old[u] + w)
return dist[dst] if dist[dst] != float('inf') else -1
与该题类似的题:
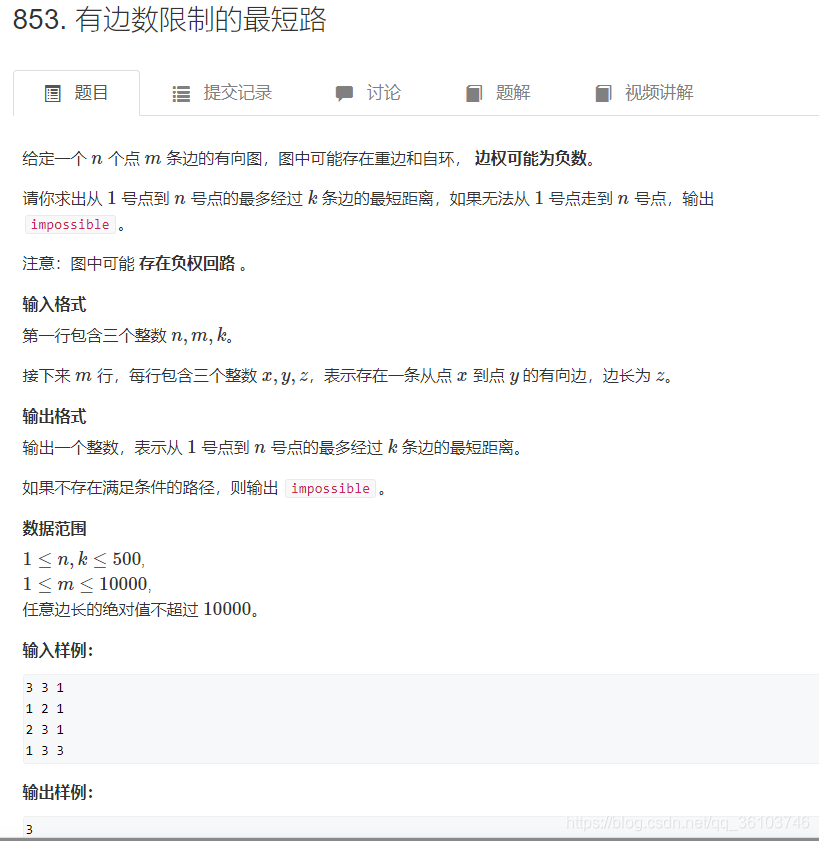
有边数限制的最短路
n, m, k = map(int, input().split())
grids = []
for _ in range(m):
grids.append(list(map(int, input().split())))
def bellmanFord(grids):
dist = [float('inf')] * (n + 1)
dist[1] = 0
for i in range(k):
dist_old = [_ for _ in dist]
for u, v, w in grids:
dist[v] = min(dist[v], dist_old[u] + w)
return dist[n] if dist[n] != float('inf') else str('impossible')
res = bellmanFord(grids)
print(res)
Bellman-Ford算法是对边进行松弛,所以这里要求最多k条边即表示最多松弛k次。如果是最多中转k个点,则表示最多松弛k+1次。