[Python知识库]Python小案例1：水仙花数及其自幂数

用Python实现，水仙花数

水仙花

水仙花数也被称为超完全数字不变数、自恋数、自幂数、阿姆斯特朗数，它是一个3位数，该数字每个位上数字的立方之和正好等于它本身。

? 自幂数是指一个 n 位数，它的每个位上的数字的 n 次幂之和等于它本身。

例如：1³ + 5³ + 3³ = 153。

1. 因为需要知道该数的各个位置数字，且是在已知三位数的情况下，那么我们就需要提取这个数的百位，十位以及个位

a = 153
# 求百位
high = a // 100
print(high)		# 1
# 求十位
mid1 = a // 10 % 10			# 第一种
mid2 = a % 100 // 10		# 第二种
print(mid1, mid2)	# 5 5
# 求个位
low = a % 10
print(low)		# 3

2. 需要在100-999之间寻找水仙花数，需要用到循环结构，并且这里明确了循环执行次数，可以使用for in循环

for num in range(100, 1000):
    low = num % 10
    mid = num // 10 % 10
    high = num // 100
    if num == low ** 3 + mid ** 3 + high ** 3:
        print(f'水仙花数有：{num}')

? 水仙花数有：153， 370， 371， 407

延伸

既然3位数有其水仙花数，那么一位数，两位数，四位数……是否有其相应的自幂数呢？

所以我们可以延伸：

一位自幂数：独身数

两位自幂数：没有

三位自幂数：水仙花数

四位自幂数：四叶玫瑰数

五位自幂数：五角星数

六位自幂数：六合数

七位自幂数：北斗七星数

八位自幂数：八仙数

九位自幂数：九九重阳数

十位自幂数：十全十美数

那么我们就可以写出一个函数可以输出各个位置的自幂数，

与水仙花数有关的函数

由于100之前，只有1-9这种独身数，所以选择从100开始遍历循环

def daffodil(num, i):
    """求正整数各个位置的i次方和(自幂数)

    :param num: 正整数（）
    :param i: 输入的数为几位数
    :return: 返回整数各个位置的i次幂
    """
    total = 0
    while num > 0:
        total += (num % 10) ** i
        num //= 10
    return total


import time

if __name__ == '__main__':
    start_time = time .time()
    for i in range(100, 10000001):
        if daffodil(i, len(str(i))) == i:
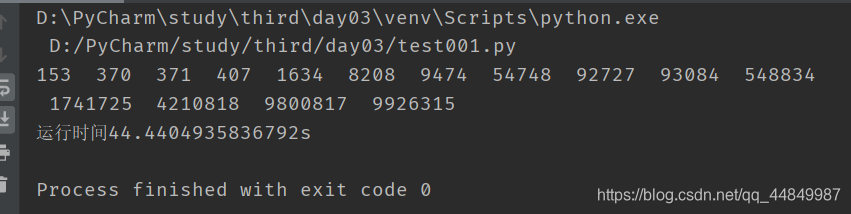
            print(i, end='  ')
    end_time = time.time()
    print()
    print(f'运行时间{end_time - start_time}s')

运行时发现运行时间太长了，所以就只能运行一下8位数以内的整数