[Python知识库]Python程序设计 实验1：Python基础练习

1. 圆柱体

编写程序，读取圆柱体的半径和高度，并使用以下公式计算圆的面积和圆柱体的体积：
面积=半径*半径*π
体积=面积*高度
例子：

Enter the radius of a cylinder: 5.5
Enter the length of a cylinder: 12
The area is 95.0331
The volume is 1140.4

（1）思路

先通过输入将圆柱的半径和高度读入，再根据公式计算出对应结果后输出。在本题中由于需要使用到pai值，可以调用math库中的pi进行计算。在输出时由于输出小数位数较多，可以使用格式化输出对输出的数字进行保留小数点后三位的操作。

（2）编程并实现

# 引用数学库以调用pai值  
import math  
# 输入圆柱的半径和高  
radius = eval(input("Enter the radius of a cylinder: "))  
length = eval(input("Enter the length of a cylinder: "))  
# 将圆柱的底面积和体积计算后输出，并保留小数点后三位  
print("The area is", format(radius**2*math.pi, '.3f'))  
print("The volume is", format(radius**2*math.pi*length, '.3f'))  

先引用数学库以调用pai值，再读入圆柱的半径和高，最后将圆柱的底面积和体积计算之后输出，并保留小数点后三位。

（3）运行并测试

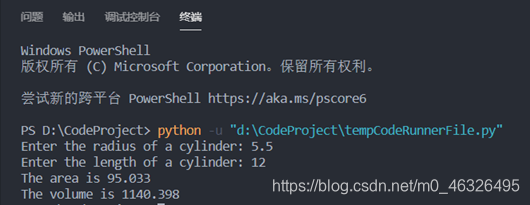
①开始运行后可以看到提示输入圆柱的半径：

②输入半径后将提示输入圆柱的高：

③输入高之后将输出圆柱的底面积和体积：

2. 整数中各位数字

编写程序，输入 0 到 1000 之间的一个整数，并将该整数中 的各位数字中的奇数相乘；如该整数不在 0 到 1000 之间，提示重新输入新数字。
例子：

Enter a number between 0 and 1000: 932
The result is 27

（1）思路

先通过输入将要处理的数字输入。再判断是否为合法数据（在0到1000）之间，如果数据合法则进入下一步操作，如果数据不合法，则通过while循环再次获取数据，直到输入数据合法为止。获取了合法的数据之后，通过每次将数字对10取模获得最低位数字，并判断是否为奇数，如果为奇数则进行累乘操作。若为偶数或已经完成奇数，则将数字变为之前的十分之一，循环处理剩余数字，直至所有数位处理完毕（剩余数为0）。此时将累乘结果输出。

（2）编程并实现

# 输入0~1000的一个数字  
num = int(input("Enter a number between 0 and 1000: "))  
  
# 如果输入的数字不合法，则重复输入，直到输入合法数字未知  
while num > 1000 or num < 0:  
    num = int(input("Invalid number, please input a number between 0 and 1000 again: "))  
  
# 通过对10取模获得最低位，并判断是否为奇数。如果是奇数则与res相乘  
res = 1  
while num > 0:  
    temp = num % 10  
    if temp % 2 != 0:  
        res *= temp  
    num = (int)(num/10)  
  
# 输出结果  
print("The result is ", res)  

先获取输入数字，并通过while实现如果输入不合法则再次输入直至数据合法的操作。通过对10取模获得最低位数字，并判断是否为奇数，若为奇数则进行累乘。若该数字不为奇数或已经完成累乘，则将原数字缩小至原数字的十分之一进行下一个数位的判断。直至所有数位都判断完毕（数字变为0），则输出累乘值。

（3）运行并测试

①开始运行后可以看到提示输入一个数字

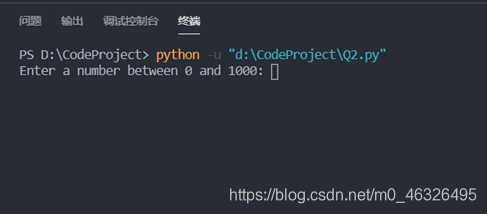
②如果输入非法，则将提示输入一个合法的数字

③输入合法数字后将计算出对应结果

3. 数字检查

编写程序，提示用户输入一个整数，并检查该数字
（1）是否可以 同时被 5 和 7 整除，
（2）是否可以被 5 或 7 整除，
（3）是否只可以被其中一个整除，但不能同时被两者整除。
例子：

Enter an integer: 35
Is 35 divisible by 5 and 7? True
Is 35 divisible by 5 or 7? True
Is 35 divisible by 5 or 7, but not both? False

（1）思路

先通过输入将要处理的数字输入。再分别判断对5和7取模之后的结果。如果全为真则能被5和7整除；如果只有一个为真，则能被5或7整除，如果都为假，则不能被5或7整除。

（2）编程并实现

# 输入0~1000的一个数字  
num = int(input("Enter an integer: "))  
  
# 判断能否被5或7整除  
flag5 = (num % 5 == 0)  
flag7 = (num % 7 == 0)  
  
# 同时被5和7整除  
if flag5 and flag7:  
    print("Is 35 divisible by 5 and 7? True")  
else:  
    print("Is 35 divisible by 5 and 7? False")  
  
# 被5或7整除  
if flag5 or flag7:  
    print("Is 35 divisible by 5 or 7? True")  
else:  
    print("Is 35 divisible by 5 or 7? False")  
  
# 只能被5或7其中之一整除  
if ((flag5 and not flag7) or (not flag5 and flag7)):  
    print("Is 35 divisible by 5 or 7, but not both? True")  
else:  
    print("Is 35 divisible by 5 or 7, but not both? False")  

先通过输入将要处理的数字输入。再分别判断对5和7取模之后的结果。如果全为真则能被5和7整除；如果只有一个为真，则能被5或7整除，如果都为假，则不能被5或7整除。

（3）运行并测试

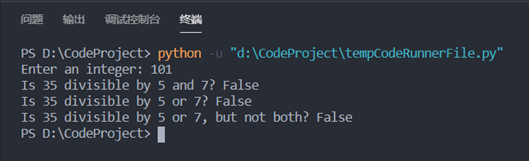
①如果输入一个只能被5整数的数字：

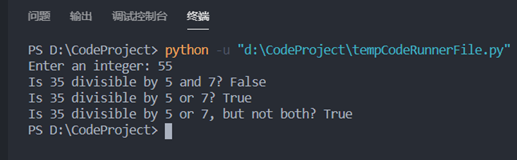
②如果输入一个只能被7整数的数字：

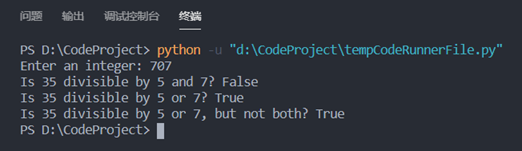
③如果输入一个既不能被5整除也不能被7整除的数字：

④如果输入一个既能被5整除也能被7整除的数字：

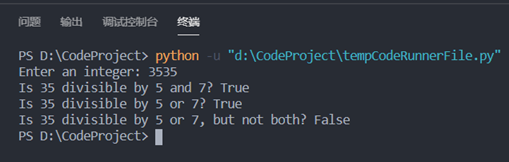
4. 三位数偶数

编写程序，输出由 1、2、5、8 这四个数字组成的每位数字都不相同的所有三位数偶数。

（1）思路

通过穷举法，将每种可能穷举出来，如果满足三个数字都不同的条件则输出并将计数器加一。

（2）编程并实现

# 定义列表以存各个数字  
num = [1, 2, 5, 8]  
  
# 定义计数器  
count = 0  
  
# 暴力穷举每一种可能  
for i in range(0, 4):  
    for j in range(0, 4):  
        for k in range(0, 4):  
            if (i != j and i != k and j != k):  
                count += 1  
                print(num[i]*100+num[j]*10+num[k])  
  
# 统计总数字个数  
print("There are", count, "different numbers.")  

通过暴力穷举每一种可能，并判断是否各个数位都不同，如果满足条件则输出并将计数加一。

（3）运行并测试

开始运行后结果输出如下：

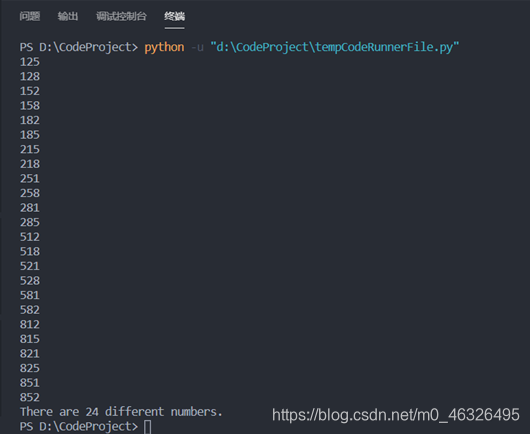
5. 百钱买汽水问题

假设大瓶汽水5元一瓶，中瓶汽水3元一瓶，小瓶汽水1元三瓶，现在有 100 块钱，想买 100 瓶汽水，列出所有的买法 （提示：4 种）。

（1）思路

暴力穷举每一种可能的购买情况，并判断是否为符合题意的购买，如果符合则将大中小各买多少瓶输出。如果不符合则进行下一组尝试。

（2）编程并实现

# 暴力穷举每一种可能  
 i in range(0, 21):  
 for j in range(0, 34):  
  
     # 如果超过100元则开始尝试下一组  
     if 5 * i + 3 * j > 100:  
         break  
  
     # 如果符合则输出  
     if i + j + (100 - 5 * i - 3 * j) * 3 == 100:  
         print("large:", i, "medium:", j,"small:", (100 - 5 * i - 3 * j) * 3)  

暴力穷举每一种购买的可能，如果符合条件则输出。

（3）运行并测试

开始运行后输出结果如下：

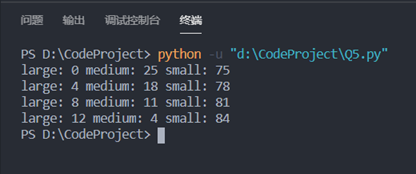
6. 乘方

编写程序，输入正整数a，按照以下格式输出乘方结果。
1 2 1
2 3 8
3 4 81
4 5 1024
5 6 15625
…
a a+1 a**(a+1)

（1）思路

先读入数字num，再通过for循环依次循环遍历每一个数值，并输出对应的数值

（2）编程并实现

# 输入num  
num = eval(input("Please input a number:"))  
for i in range(1, num+1):  
    print(i, i + 1, i ** (i + 1))  

先输入num，并利用for循环进行遍历依次输出

（3）运行并测试

①开始运行程序，将提示输入一个数字：

②输入对应数字后将输出对应乘方：

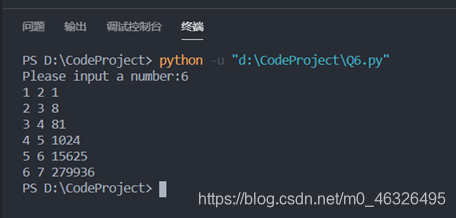
7. 阶乘

编写代码以按相反顺序打印阶乘结果。例如输入 n=10，文字输出为小于等于n的所有合数的阶乘（注：n的阶乘是123*…*n；不能使用math.factorial() 函数）。
10!: 3628800
9!: 362880
8!: 40320
6!: 720
4!: 24

（1）思路

先读入数字num，再通过for循环利用做差完成反向运算，对于每一个数字，通过for循环依次做除法判断是否为其因子的方式来判断是否为合数，如果是合数则再利用for循环计算阶乘，如果不是，则判断下一个数字。

（2）编程并实现

# 输入num  
num = eval(input("Please input a number:"))  
  
# 通过for进行遍历判断并输出  
for i in range(1, num + 1):  
  
    # 如果小于等于2 一定不是合数  
    if num + 1 - i <= 2:  
        continue  
  
    # 循环做除法判断是否为质数  
    flag = 2  
    while flag < num - i:  
        if (num + 1 - i) % flag == 0:  
            break  
        flag += 1  
  
    # 如果是质数  
    if flag == num - i:  
        continue  
  
    # 是合数则输出  
    print(num + 1 - i, end="")  
    print("!:", end="")  
    res = 1  
  
    # 通过循环计算阶乘  
    for j in range(1, num + 2 - i):  
        res *= j  
    print(res)  

先输入数字，然后通过for循环进行依次循环判断，此处为了实现倒序输出，需要进行做差。获取输入后，对于每一个数字，先通过for循环来判断是否为合数，如果是合数则再通过for循环计算阶乘并输出，如果不是，则对下一个数进行判断。

（3）运行并测试

①编写

② 输入对应数字后将计算并输出结果：

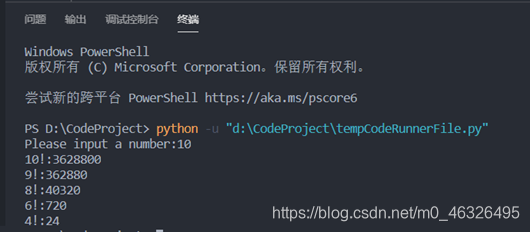
8. 计算最大公约数

找到两个整数的最大公约数 (the greatest common divisor: GCD)
例子：

Enter the first number: 12
Enter the second number: 6
GCD of 12 and 6 is 6

（1）思路

先读入两个数字，然后通过欧几里得辗转相除法计算最大公约数。

（2）编程并实现

   # 输入两个数字  
a = num1 = eval(input("Enter the first number: "))  
b = num2 = eval(input("Enter the second number: "))  
  
# 利用欧几里得辗转相除法计算最大公因数  
temp = num1 % num2  
while temp != 0:  
    num1 = num2  
    num2 = temp  
    temp = num1 % num2  
  
# 输出结果  
print("GCD of", a, "and", b, "is", num2)  

先输入数字，然后通过欧几里得辗转相除算法获取最大公因数。

（3）运行并测试

①运行程序，将提示输入两个数字：

②输入完成后即输出结果：

实验结论

通过本次实验，我学会了Python的基本语法，循环，判断等使用，学会了使用Python对代码进行编写。也明白了Python与之前学习的C/C++，Java有一些不同之处，比如嵌套关系使用缩进而不是使用大括号表示等等。
在本次编程过程中，也遇到了一些问题：

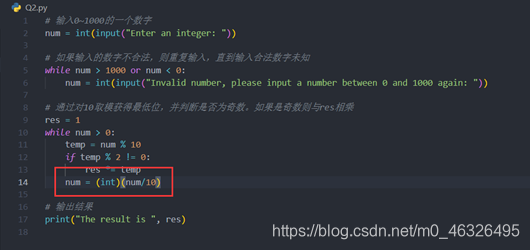
1. 由于Python有数据类型自动识别，有时会产生不必要的精度损失，需要进行类型的强制转换，比如本次实验的第二题，如果不对num进行类型转换，将发生精度损失而导致错误。
   
   

2. 要对特殊数据进行特殊分析。在编写第七题的代码时，最开始忘记考虑1既不是质数也不是合数而发生错误
   这些都告诉我们，在进行代码编写的过程中，务必要认真仔细，如果不仔细可能会发生失之毫厘谬以千里的事情！