自己写的cuda函数和cublas和ispc的对比
!!!代码在文末 !!!
开文废话
憋了这么久,终于开始写了。
预备知识
因为cublas的数据存储是按照列优先的,而c/c++是按行存储的。
行优先还是列优先
首先了解“行优先”和“列优先”的知识,这两种方式在数学上的直观描述如下,给定如下矩阵:
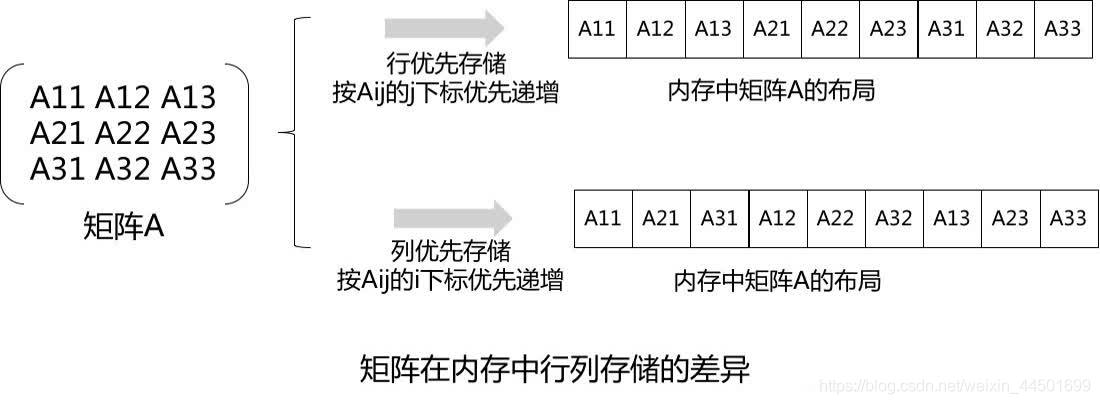
矩阵在逻辑上表达为2维的矩阵,M行K列,但存储到内存的时候都是按一维布局,其中按行优先存储和按列优先存储的差异如上图所示

如上图所示,当矩阵按行优先存储然后又按相反的列优先读取的话,就会得到原矩阵转置的结果;同理适用于按列优先存储然后按行优先读取。
例 cublasSgemm 函数
cublasStatus_t cublasSgemm(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const float *alpha,
const float *A, int lda,
const float *B, int ldb,
const float *beta,
float *C, int ldc)
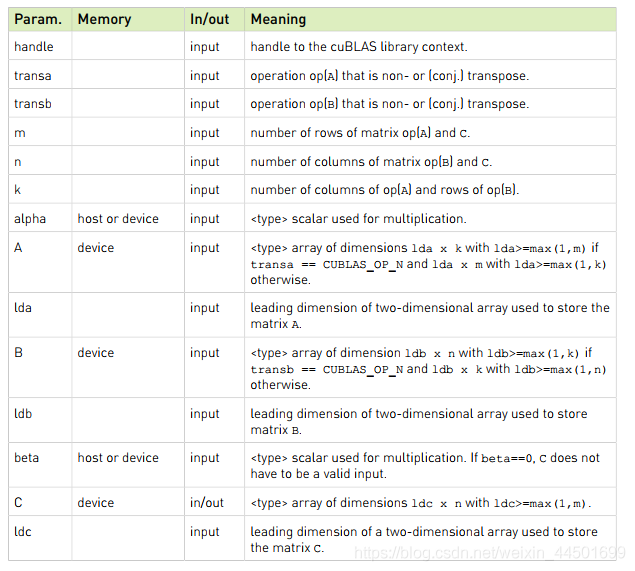
cublasSgemm的官方API说明文档链接cublas
-
根据文档说可以知道,cublasSgemm完成了 C = alpha * op ( A ) * op ( B ) + beta * C 的矩阵乘、加运算。
-
其中alpha和beta是标量, A、 B、 C是以列优先存储的矩阵,A称为乘法左矩阵、B称为乘法右矩阵、C称为结果矩阵,当alpha = 1.0f 并且 beta =0.0f 的时候 cublasSgemm完成了计算:
结果矩阵= op (乘法左矩阵) * op ( 乘法右矩阵)。 -
cublasOperation_t 该类型表明输入的密集矩阵的形式,其值有 CUBLAS_OP_N(非转置);CUBLAS_OP_T(转置); CUBLAS_OP_C(共轭转置)。该函数对应于BLAS(FORTRAN版)的变量字符’N’或’n’(非转置,即正常形式的矩阵),T’或’t’(转置矩阵);‘C’或’c’(共轭转置矩阵,对应的是复数矩阵。
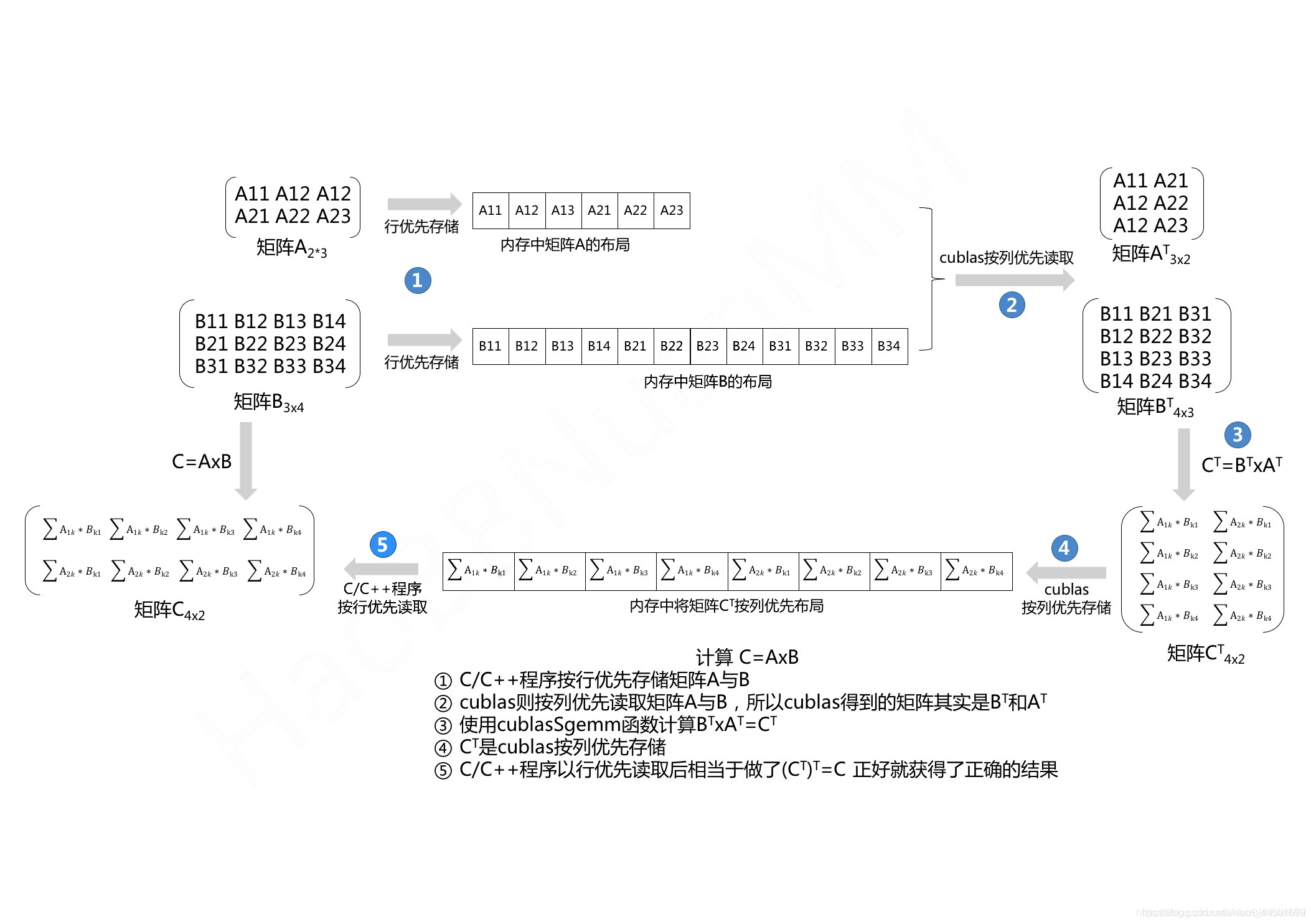
求解C=AxB
其中(A为A_ROW行A_COL列 B为B_ROW行B_COL列 所以 C为A_ROW行B_COL列)
不使用cublasSgemm transa与transb参数
由于C/C++程序中输入的A和B是按行存储,所以在的情况下,cublas其实读取到的是A和B的转置矩阵AT和BT.
根据线性代数的规则可知CT = (A x B)T = BT x AT 所以cublasSgemm API中几个参数设置如下:
- 设置了cublasSgemm的transa与transb参数=CUBLAS_OP_N
- 乘法左矩阵为BT=参数设置为B,乘法右矩阵为AT=参数设置为A
- 结果矩阵的行数为CT的行数(正常c/c++矩阵的列数)= 参数设置为:B_COL
- 结果矩阵的列数为CT的列数(正常c/c++矩阵的行数)= 参数设置为:A_ROW
- 乘法左矩阵列与乘法右矩阵的行=参数设置为:B_ROW
- 按列优先读取乘法左矩阵B的主维度(即BT有几行、正常c/c++矩阵的列数)=参数设置为B_COL
- 按列优先读取乘法右矩阵A的主维度(即AT有几行、正常c/c++矩阵的列数)=参数设置为A_COL
- 结果矩阵存储在参数C中,它的主维度(即结果矩阵c有几行)= 参数设置为B_COL
cublasSgemm(
handle,
CUBLAS_OP_N, //矩阵A的属性参数,不转置,按列优先
CUBLAS_OP_N, //矩阵B的属性参数,不转置,按列优先
B_COL, //矩阵BT、CT的行数
A_ROW, //矩阵AT、CT的列数
B_ROW, //BT的列数,AT的行数,此处也可为A_COL,一样的
&a, //alpha的值
d_B, //左矩阵,为B^T
B_COL, //B^T的leading dimension,按列优先,则leading dimension为B^T的行数(B的列数)
d_A, //右矩阵,为A^T
A_COL, //A^T的leading dimension,按列优先,则leading dimension为A^T的行数(A的列数)
&b, //beta的值
d_C, //结果矩阵C
B_COL //C^T的leading dimension,C^T矩阵一定按列优先,则leading dimension为C^T的行数(C的列数)
);//此处的h_C是按列存储的CT
按上面的参数调用cublasSgemm API (矩阵A按行存储在指针d_A, 矩阵B按行存储在指针d_B, 矩阵C的存储空间指针d_C) 最后结果d_C传输到host端的h_C,从结果矩阵的存储空间h_C中按行读取到的就是C=AxB的结果,整个cublasSgemm的计算过程如下图所示。
部分示例代码:
template <typename T1, typename T2>
void cublas_kernel()
{
// 定义状态变量
cublasHandle_t handle;
cublasCreate(&handle);
cudaEventCreate(&start);
cudaEventCreate(&stop);
//存储于内存中的矩阵
T1* h_A, * h_B;
T2* h_C, * h_CC;
//在内存中开辟空间
cudaHostAlloc((void**)&h_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_CC, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
MatrixINIT<T1>(A_ROW, A_COL, h_A);
MatrixINIT<T1>(B_ROW, B_COL, h_B);
// 打印待测试的矩阵
#if defined(USE_FLOAT_T)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#elif defined(USE_FLOAT_N)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#elif defined(USE_DOUBLE_T)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#elif defined(USE_DOUBLE_N)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#endif
//存储于显存中的矩阵
T1* d_A, * d_B;
T2* d_C;
cudaMalloc((void**)&d_A, sizeof(T1) * A_ROW * A_COL);
cudaMalloc((void**)&d_B, sizeof(T1) * B_ROW * B_COL);
cudaMalloc((void**)&d_C, sizeof(T2) * A_ROW * B_COL);
/*
cudaHostAlloc((void**)&d_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
*/
//创建流对象,用于任务级(Grid)同步
cudaStream_t stream;
cudaStreamCreateWithFlags(&stream, cudaStreamNonBlocking);
cublasSetStream(handle, stream);
const T2 a = 1.0f, b = 0.0f;
//计时开始
TIMER_START(_X);
//cudaEventRecord(start, 0);
for (int i = 0; i < N ; i++)
{
//数据从Host端拷贝到Device端、 cubals方式
/*
cublasSetMatrix(A_ROW, A_COL, sizeof(*h_A), h_A, A_ROW, d_A, A_ROW);
cublasSetMatrix(B_ROW, B_COL, sizeof(*h_B), h_B, B_ROW, d_B, B_ROW);
*/
cublasSetMatrixAsync(A_ROW, A_COL, sizeof(*h_A), h_A, A_ROW, d_A, A_ROW, stream);
cublasSetMatrixAsync(B_ROW, B_COL, sizeof(*h_B), h_B, B_ROW, d_B, B_ROW, stream);
//数据从Host端拷贝到Device端、 传统方式
//cudaMemcpy(d_A, H_A, sizeof(T1) * A_ROW * A_COL, cudaMemcpyHostToDevice);
//cudaMemcpy(d_B, H_B, sizeof(T1) * B_ROW * B_COL, cudaMemcpyHostToDevice);
//单独计算核函数运算时间
cudaEventRecord(start, 0);
#if defined(USE_FLOAT_N)
cublasSgemm(
handle,
CUBLAS_OP_N, //矩阵A的属性参数,不转置,按列优先
CUBLAS_OP_N, //矩阵B的属性参数,不转置,按列优先
B_COL, //矩阵B^T、C^T的行数
A_ROW, //矩阵A^T、C^T的列数
B_ROW, //B^T的列数,A^T的行数,此处也可为A_COL,一样的
&a, //alpha的值
d_B, //左矩阵,为B^T
B_COL, //B^T的leading dimension,按列优先,则leading dimension为B^T的行数(B的列数)
d_A, //右矩阵,为A^T
A_COL, //A^T的leading dimension,按列优先,则leading dimension为A^T的行数(A的列数)
&b, //beta的值
d_C, //结果矩阵C
B_COL //C^T的leading dimension,C^T矩阵一定按列优先,则leading dimension为C^T的行数(C的列数)
);//此处的h_C是按列存储的C^T
#elif defined(USE_DOUBLE_N)
cublasDgemm(
handle,
CUBLAS_OP_N, //矩阵A的属性参数,不转置,按列优先
CUBLAS_OP_N, //矩阵B的属性参数,不转置,按列优先
B_COL, //矩阵B^T、C^T的行数
A_ROW, //矩阵A^T、C^T的列数
B_ROW, //B^T的列数,A^T的行数,此处也可为A_COL,一样的
&a, //alpha的值
d_B, //左矩阵,为B^T
B_COL, //B^T的leading dimension,按列优先,则leading dimension为B^T的行数(B的列数)
d_A, //右矩阵,为A^T
A_COL, //A^T的leading dimension,按列优先,则leading dimension为A^T的行数(A的列数)
&b, //beta的值
d_C, //结果矩阵C
B_COL //C^T的leading dimension,C^T矩阵一定按列优先,则leading dimension为C^T的行数(C的列数)
);//此处的h_C是按列存储的C^T
#endif
//计时结束
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime, start, stop);
//TIMER_STOP(_X);
//cout << "GPU耗费了: " << TIMER_MSEC(_X) << " ms " << "\n";
//
//将Device端计算完的结果传输会Host端 cublas方式
//cublasGetMatrix(A_ROW, B_COL, sizeof(*h_C), d_C, A_ROW, h_C, A_ROW);
cublasGetMatrixAsync(A_ROW, B_COL, sizeof(*h_C), d_C, A_ROW, h_C, A_ROW, stream);
//传统方式
//cudaMemcpy(H_C, d_C, sizeof(T2) * A_ROW * B_COL, cudaMemcpyDeviceToHost);
}
TIMER_STOP(_X);
/*
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime_cublas, start, stop);
*/
//打印结果
cout << "cublas_kernel GPU传输、计算花费了: " << TIMER_MSEC(_X) << " ms " << "\n";
//std::cout<< "GPU传输、计算花费了:" << elapsedTime_cublas << " ms" << std::endl;
std::cout << "cublas_kernel GPU计算花费了:" << elapsedTime * N<< " ms" << std::endl<< std::endl;
#if defined(USE_FLOAT_N)
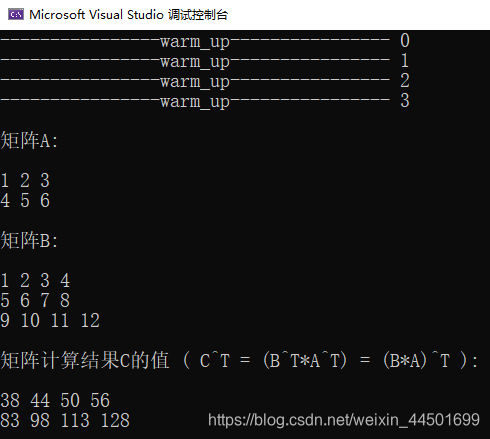
//按行读取h_C相当于做了CTT=C的结果
Matrixshow<T2>("计算结果C的值 ( C^T = (B^T*A^T) = (B*A)^T )", A_ROW, B_COL, h_C, 1, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 0);
#endif
#elif defined(USE_DOUBLE_N)
//按行读取h_C相当于做了CTT=C的结果
Matrixshow<T2>("计算结果C的值 ( C^T = (B^T*A^T) = (B*A)^T )", A_ROW, B_COL, h_C, 1, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 0);
#endif
#endif
//释放内存
cudaFree(d_A);
cudaFree(d_B);
cudaFree(d_C);
/*
cudaFreeHost(d_A);
cudaFreeHost(d_B);
cudaFreeHost(d_C);
*/
cudaFreeHost(h_A);
cudaFreeHost(h_B);
cudaFreeHost(h_C);
cudaFreeHost(h_CC);
cublasDestroy(handle);
cudaEventDestroy(start);
cudaEventDestroy(stop);
cudaStreamDestroy(stream);
}
使用cublasSgemm transa与transb参数
由于C/C++程序中输入的A和B是按行存储,所以在的情况下,cublas其实读取到的是A和B的转置矩阵A^T
和 B^T
设置了cublasSgemm的transa与transb参数后,可以在做矩阵运算前对读取到的A^T、
B^T矩阵做一次转置,获得A和B根据线性代数的规则可知C = A x B 所以cublasSgemm API中几个参数设置如下:
- 设置了cublasSgemm的transa与transb参数=CUBLAS_OP_T,在进行矩阵运算前对读取的矩阵做一次转置
- 乘法左矩阵为A=参数设置为A,乘法右矩阵为B=参数设置为B
- 结果矩阵的行数为C的行数=参数设置为 A_ROW
- 结果矩阵的列数为C的列数=参数设置为 B_COL
- 乘法左矩阵列与乘法右矩阵的行=参数设置为 A_COL
- 按列优先读取乘法左矩阵A的主维度(就变成了类似CUBLAS_OP_N的参数情况)(即A^T有几行)=参数设置为 A_COL
- 按列优先读取乘法右矩阵B的主维度(就变成了类似CUBLAS_OP_N的参数情况)(即B^T有几行)=参数设置为 B_COL
- 结果矩阵存储在参数C中,它的主维度(即结果矩阵c有几行)= 参数设置为 A_ROW
cublasSgemm(
handle,
CUBLAS_OP_T, //矩阵A的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
CUBLAS_OP_T, //矩阵B的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
A_ROW, //矩阵A、C的行数
B_COL, //矩阵B、C的列数
A_COL, //A的列数,B的行数,此处也可为B_ROW一样的
&a, //alpha的值
d_A, //左矩阵,为A
A_COL, //A的leading dimension,按列优先,则leading dimension为(A^T的行数)A的列数
d_B, //右矩阵,为B
B_COL, //B的leading dimension,按列优先,则leading dimension为(B^T的行数)A的列数
&b, //beta的值
d_C, //结果矩阵C
A_ROW//C的leading dimension,C矩阵一定按列优先,则leading dimension为C的行数
);//此处的h_C是按列存储的C
红色的参数标记出与“不使用cublasSgemm transa与transb参数”例子中的不同,按上面的参数调用cublasSgemm API (矩阵A按行存储在指针d_a, 矩阵B按行存储在指针d_b, 矩阵C的存储空间指针d_c) 最后从结果矩阵的存储空间d_c中按行读取到的就是C=AxB后C^T
的结果,所以在C/C++程序中还需要对读取的结果C^T做一次矩阵转置操作才能获得最终正确的C。整个cublasSgemm的计算过程如下图所示:
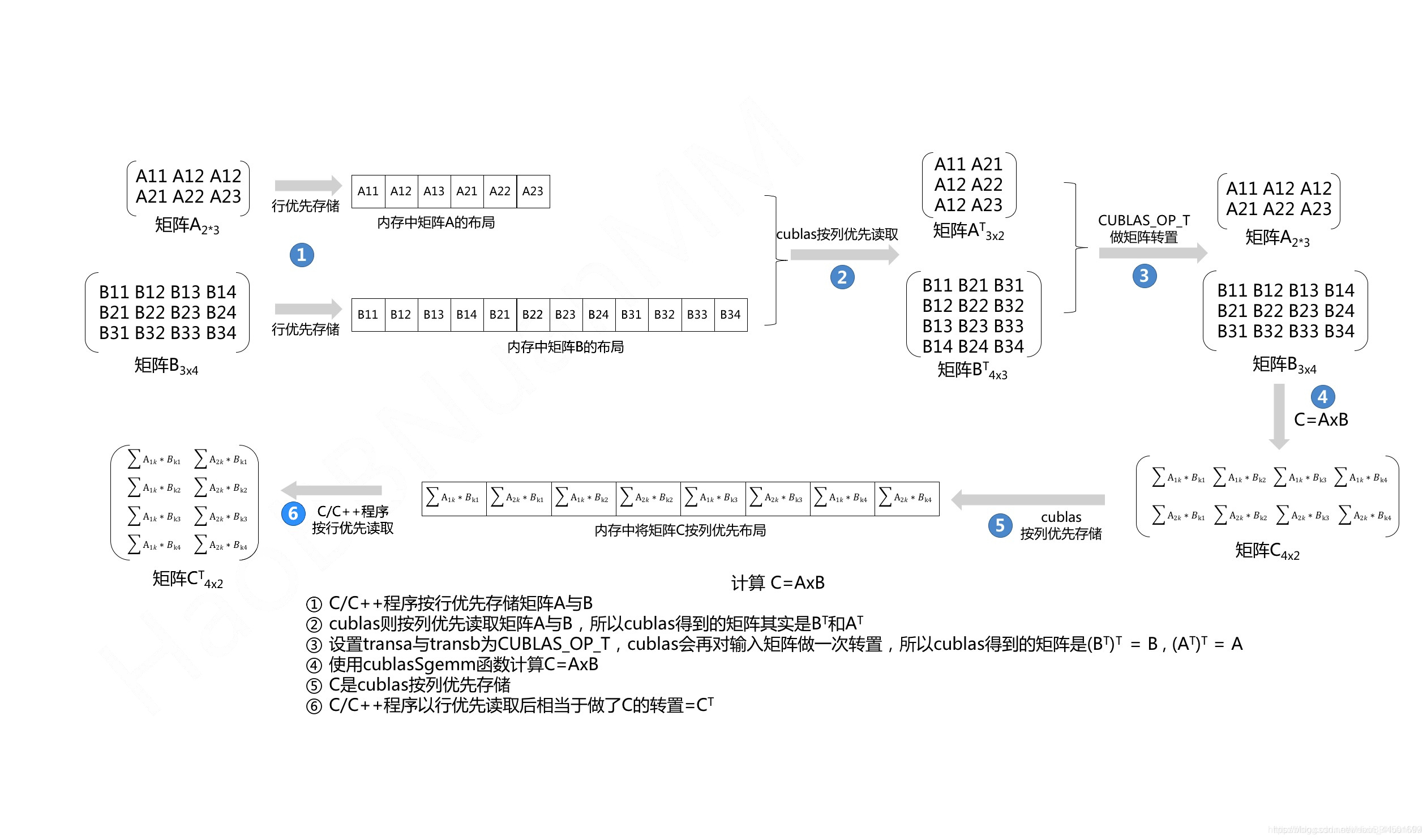
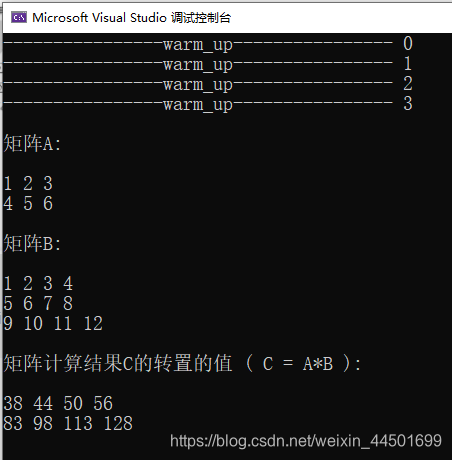
结果:
部分示例代码
template <typename T1, typename T2>
void cublas_kernel()
{
// 定义状态变量
cublasHandle_t handle;
cublasCreate(&handle);
cudaEventCreate(&start);
cudaEventCreate(&stop);
//存储于内存中的矩阵
T1* h_A, * h_B;
T2* h_C, * h_CC;
//在内存中开辟空间
cudaHostAlloc((void**)&h_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_CC, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
MatrixINIT<T1>(A_ROW, A_COL, h_A);
MatrixINIT<T1>(B_ROW, B_COL, h_B);
// 打印待测试的矩阵
#if defined(USE_FLOAT_T)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 1);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 1);
#elif defined(USE_FLOAT_N)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#elif defined(USE_DOUBLE_T)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#elif defined(USE_DOUBLE_N)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#endif
//存储于显存中的矩阵
T1* d_A, * d_B;
T2* d_C;
cudaMalloc((void**)&d_A, sizeof(T1) * A_ROW * A_COL);
cudaMalloc((void**)&d_B, sizeof(T1) * B_ROW * B_COL);
cudaMalloc((void**)&d_C, sizeof(T2) * A_ROW * B_COL);
/*
cudaHostAlloc((void**)&d_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
*/
//创建流对象,用于任务级(Grid)同步
cudaStream_t stream;
cudaStreamCreateWithFlags(&stream, cudaStreamNonBlocking);
cublasSetStream(handle, stream);
const T2 a = 1.0f, b = 0.0f;
//计时开始
TIMER_START(_X);
//cudaEventRecord(start, 0);
for (int i = 0; i < N ; i++)
{
//数据从Host端拷贝到Device端、 cubals方式
/*
cublasSetMatrix(A_ROW, A_COL, sizeof(*h_A), h_A, A_ROW, d_A, A_ROW);
cublasSetMatrix(B_ROW, B_COL, sizeof(*h_B), h_B, B_ROW, d_B, B_ROW);
*/
cublasSetMatrixAsync(A_ROW, A_COL, sizeof(*h_A), h_A, A_ROW, d_A, A_ROW, stream);
cublasSetMatrixAsync(B_ROW, B_COL, sizeof(*h_B), h_B, B_ROW, d_B, B_ROW, stream);
//数据从Host端拷贝到Device端、 传统方式
//cudaMemcpy(d_A, H_A, sizeof(T1) * A_ROW * A_COL, cudaMemcpyHostToDevice);
//cudaMemcpy(d_B, H_B, sizeof(T1) * B_ROW * B_COL, cudaMemcpyHostToDevice);
//单独计算核函数运算时间
cudaEventRecord(start, 0);
#if defined(USE_FLOAT_T)
cublasSgemm(
handle,
CUBLAS_OP_T, //矩阵A的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
CUBLAS_OP_T, //矩阵B的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
A_ROW, //矩阵A、C的行数
B_COL, //矩阵B、C的列数
A_COL, //A的列数,B的行数,此处也可为B_ROW一样的
&a, //alpha的值
d_A, //左矩阵,为A
A_COL, //A的leading dimension,按列优先,则leading dimension为(A^T的行数)A的列数
d_B, //右矩阵,为B
B_COL, //B的leading dimension,按列优先,则leading dimension为(B^T的行数)A的列数
&b, //beta的值
d_C, //结果矩阵C
A_ROW //C的leading dimension,C矩阵一定按列优先,则leading dimension为C的行数
);//此处的h_C是按列存储的C
#elif defined(USE_DOUBLE_T)
cublasDgemm(
handle,
CUBLAS_OP_T, //矩阵A的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
CUBLAS_OP_T, //矩阵B的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
A_ROW, //矩阵A、C的行数
B_COL, //矩阵B、C的列数
A_COL, //A的列数,B的行数,此处也可为B_ROW一样的
&a, //alpha的值
d_A, //左矩阵,为A
A_COL, //A的leading dimension,按列优先,则leading dimension为(A^T的行数)A的列数
d_B, //右矩阵,为B
B_COL, //B的leading dimension,按列优先,则leading dimension为(B^T的行数)A的列数
&b, //beta的值
d_C, //结果矩阵C
A_ROW //C的leading dimension,C矩阵一定按列优先,则leading dimension为C的行数
);//此处的h_C是按列存储的C
#endif
//计时结束
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime, start, stop);
//TIMER_STOP(_X);
//cout << "GPU耗费了: " << TIMER_MSEC(_X) << " ms " << "\n";
//
//将Device端计算完的结果传输会Host端 cublas方式
//cublasGetMatrix(A_ROW, B_COL, sizeof(*h_C), d_C, A_ROW, h_C, A_ROW);
cublasGetMatrixAsync(A_ROW, B_COL, sizeof(*h_C), d_C, A_ROW, h_C, A_ROW, stream);
//传统方式
//cudaMemcpy(H_C, d_C, sizeof(T2) * A_ROW * B_COL, cudaMemcpyDeviceToHost);
}
TIMER_STOP(_X);
/*
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime_cublas, start, stop);
*/
//打印结果
cout << "cublas_kernel GPU传输、计算花费了: " << TIMER_MSEC(_X) << " ms " << "\n";
//std::cout<< "GPU传输、计算花费了:" << elapsedTime_cublas << " ms" << std::endl;
std::cout << "cublas_kernel GPU计算花费了:" << elapsedTime * N<< " ms" << std::endl<< std::endl;
#if defined(USE_FLOAT_T)
// 按行优先顺序读取h_C相当于做了CT的结果
Matrixshow<T2>("计算结果C的转置的值 ( C = A*B )", A_ROW, B_COL, h_C, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 1);
#endif
#elif defined(USE_DOUBLE_T)
// 按行优先顺序读取h_C相当于做了CT的结果
Matrixshow<T2>("计算结果C的转置的值 ( C = A*B )", A_ROW, B_COL, h_C, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 1);
#endif
#endif
//释放内存
cudaFree(d_A);
cudaFree(d_B);
cudaFree(d_C);
/*
cudaFreeHost(d_A);
cudaFreeHost(d_B);
cudaFreeHost(d_C);
*/
cudaFreeHost(h_A);
cudaFreeHost(h_B);
cudaFreeHost(h_C);
cudaFreeHost(h_CC);
cublasDestroy(handle);
cudaEventDestroy(start);
cudaEventDestroy(stop);
cudaStreamDestroy(stream);
}
cublasGemmEx的使用
但是GPU的内存一般比较有限,实际项目中,为了能够做更大的矩阵乘法,使用FP32型数据占用空间会很大,所以可以压缩为int8型数据进行矩阵乘法运算,这时使用的接口模型为:
cublasStatus_t cublasGemmEx(cublasHandle_t handle, //句柄
cublasOperation_t transa, //a矩阵转置选项
cublasOperation_t transb, //b矩阵转置选项
int m, //a矩阵行数
int n, //b矩阵列数
int k, //a矩阵列数兼b矩阵行数
const void *alpha, //乘法因子alpha
const void *A, //A矩阵
cudaDataType_t Atype, //A矩阵的数据类型
int lda, //A矩阵的列数
const void *B, //B矩阵
cudaDataType_t Btype, //B矩阵的数据类型
int ldb, //B矩阵的行数
const void *beta, //乘法因子beta
void *C, //C结果矩阵
cudaDataType_t Ctype, //C结果矩阵数据类型
int ldc, //C矩阵的行数
cudaDataType_t computeType, //计算模式
cublasGemmAlgo_t algo)
该矩阵接口和cublasSgemm几乎相同,但多了几个参数:cudaDataType_t Atype A矩阵数据类型、cudaDataType_t Btype B矩阵数据类型、cudaDataType_t Ctype C矩阵数据类型以及cudaDataType_t computeType 计算模式和cublasGemmAlgo_t参数。首先来说,这个接口可以完成的运算表达式如下:
C=αop(A)op(B)+βC
其中,α和β为标量,A、B、C分别是m×k、k×n、m×n的矩阵,当α = 1, β = 0时,即为:
C=op(A)op(B)
也就是做矩阵乘法。α和β分别对应cublasGemmEx中的const void *alpha、const void *beta,这一点与前面cublasSegmm做FP32类型的接口是一样的。
在接口中,cublasOperation_t transa矩阵转置选项有如下三种:
-
transa == CUBLAS_OP_N表示A矩阵,无任何转置。
-
transa == CUBLAS_OP_T表示A^T,A的转置。
-
transa == CUBLAS_OP_C表示A^H,A的共轭转置。
同理,B矩阵也是一样。
在接口中,新增的cudaDataType_t Atype A矩阵数据类型、cudaDataType_t Btype B矩阵数据类型、cudaDataType_t Ctype C矩阵数据类型以及cudaDataType_t computeType这几个参数的取值情况如下表所示:
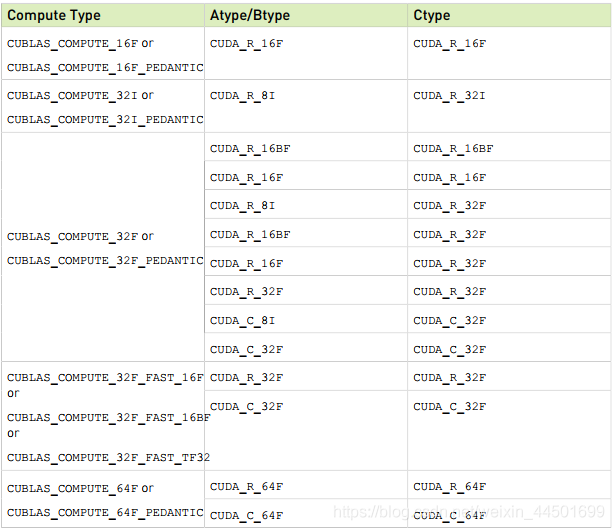
我们这里选择的int8型矩阵乘法,最好选择Atype/Btype为CUDA_R_8I型,计算模式CUDA_R_32I,乘出的结果Ctype为CUDA_R_32I类型。最后的cublasGemmAlgo_t参数可以选择的值如下表所示:
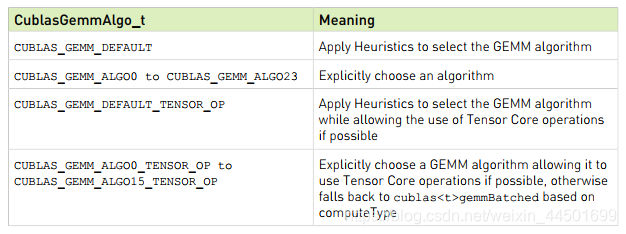
这里可以选择CUBLAS_GEMM_DEFAULT,应用启发式选择GEMM算法。
部分示例代码
cublasGemmEX函数做int8型矩阵乘法实现:
template <typename T1, typename T2>
void cublas_kernel()
{
// 定义状态变量
cublasHandle_t handle;
cublasCreate(&handle);
cudaEventCreate(&start);
cudaEventCreate(&stop);
//存储于内存中的矩阵
T1* h_A, * h_B;
T2* h_C, * h_CC;
//在内存中开辟空间
cudaHostAlloc((void**)&h_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_CC, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
MatrixINIT<T1>(A_ROW, A_COL, h_A);
MatrixINIT<T1>(B_ROW, B_COL, h_B);
// 打印待测试的矩阵
#if defined(USE_INT8_T)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0, 0, "char");
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0, 0,"char");
#elif defined(USE_INT8_N)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0, 0, "char");
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0, 0, "char");
#endif
//存储于显存中的矩阵
T1* d_A, * d_B;
T2* d_C;
cudaMalloc((void**)&d_A, sizeof(T1) * A_ROW * A_COL);
cudaMalloc((void**)&d_B, sizeof(T1) * B_ROW * B_COL);
cudaMalloc((void**)&d_C, sizeof(T2) * A_ROW * B_COL);
/*
cudaHostAlloc((void**)&d_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
*/
//创建流对象,用于任务级(Grid)同步
cudaStream_t stream;
cudaStreamCreateWithFlags(&stream, cudaStreamNonBlocking);
cublasSetStream(handle, stream);
const T2 a = 1.0f, b = 0.0f;
//计时开始
TIMER_START(_X);
//cudaEventRecord(start, 0);
for (int i = 0; i < N ; i++)
{
//数据从Host端拷贝到Device端、 cubals方式
/*
cublasSetMatrix(A_ROW, A_COL, sizeof(*h_A), h_A, A_ROW, d_A, A_ROW);
cublasSetMatrix(B_ROW, B_COL, sizeof(*h_B), h_B, B_ROW, d_B, B_ROW);
*/
cublasSetMatrixAsync(A_ROW, A_COL, sizeof(*h_A), h_A, A_ROW, d_A, A_ROW, stream);
cublasSetMatrixAsync(B_ROW, B_COL, sizeof(*h_B), h_B, B_ROW, d_B, B_ROW, stream);
//数据从Host端拷贝到Device端、 传统方式
//cudaMemcpy(d_A, H_A, sizeof(T1) * A_ROW * A_COL, cudaMemcpyHostToDevice);
//cudaMemcpy(d_B, H_B, sizeof(T1) * B_ROW * B_COL, cudaMemcpyHostToDevice);
//单独计算核函数运算时间
cudaEventRecord(start, 0);
#if defined(USE_INT8_T)
cublasGemmEx(handle, //句柄
CUBLAS_OP_T, //矩阵A的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
CUBLAS_OP_T, //矩阵B的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
A_ROW, //矩阵A、C的行数
B_COL, //矩阵B、C的列数
A_COL, //A的列数,B的行数,此处也可为B_ROW一样的
&a, //运算式的 α 值
d_A, //A矩阵
CUDA_R_8I, //A矩阵计算模式,int8型
A_COL, //A的leading dimension,按行优先存储,读取还是列优先,则leading dimension为(A^T的行数)A的列数
d_B, //B矩阵
CUDA_R_8I, //B矩阵计算模式,int8型
B_COL, //B的leading dimension,按行优先存储,读取还是列优先,则leading dimension为(B^T的行数)A的列数
&b, //乘法因子beta
d_C, //C结果矩阵
CUDA_R_32I, //C矩阵计算模式,int32型
A_ROW, //C的leading dimension,C矩阵一定按列优先,则leading dimension为C的行数
CUDA_R_32I, //计算模式,int32模式
//CUBLAS_GEMM_ALGO2 //算法参数
CUBLAS_GEMM_DFALT
); //此处的h_C是按列存储的C
#endif
//计时结束
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime, start, stop);
//TIMER_STOP(_X);
//cout << "GPU耗费了: " << TIMER_MSEC(_X) << " ms " << "\n";
//
//将Device端计算完的结果传输会Host端 cublas方式
//cublasGetMatrix(A_ROW, B_COL, sizeof(*h_C), d_C, A_ROW, h_C, A_ROW);
cublasGetMatrixAsync(A_ROW, B_COL, sizeof(*h_C), d_C, A_ROW, h_C, A_ROW, stream);
//传统方式
//cudaMemcpy(H_C, d_C, sizeof(T2) * A_ROW * B_COL, cudaMemcpyDeviceToHost);
}
TIMER_STOP(_X);
/*
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime_cublas, start, stop);
*/
//打印结果
cout << "cublas_kernel GPU传输、计算花费了: " << TIMER_MSEC(_X) << " ms " << "\n";
//std::cout<< "GPU传输、计算花费了:" << elapsedTime_cublas << " ms" << std::endl;
std::cout << "cublas_kernel GPU计算花费了:" << elapsedTime * N<< " ms" << std::endl<< std::endl;
#if defined(USE_INT8_T)
// 按行优先顺序读取h_C相当于做了CT的结果
//Matrixshow<T2>("计算结果C的转置的值 ( C = A*B )", A_ROW, B_COL, h_C, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 1);
#endif
#elif defined(USE_INT8_N)
//按行读取h_C相当于做了CTT=C的结果
//Matrixshow<T2>("计算结果C的值 ( C^T = (B^T*A^T) = (B*A)^T )", A_ROW, B_COL, h_C, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 0);
#endif
#endif
//释放内存
cudaFree(d_A);
cudaFree(d_B);
cudaFree(d_C);
/*
cudaFreeHost(d_A);
cudaFreeHost(d_B);
cudaFreeHost(d_C);
*/
cudaFreeHost(h_A);
cudaFreeHost(h_B);
cudaFreeHost(h_C);
cudaFreeHost(h_CC);
cublasDestroy(handle);
cudaEventDestroy(start);
cudaEventDestroy(stop);
cudaStreamDestroy(stream);
}
当运行有误时,可以打印cublasGemmEx的返回值来确认是什么错误,官方定义的错误码如下表所示:
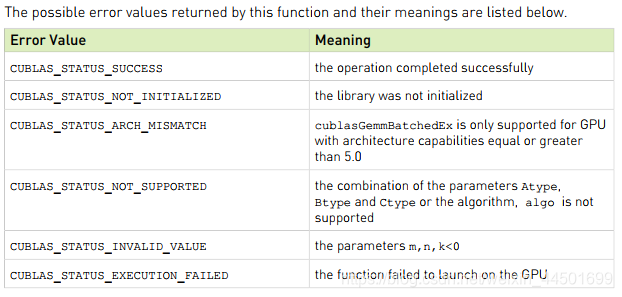
成功时会返回0,也就是CUBLAS_STATUS_SUCCESS。多数情况会返回CUBLAS_STATUS_INVALID_VALUE,这就是m,n,k参数传入不正确所致。
运行结果
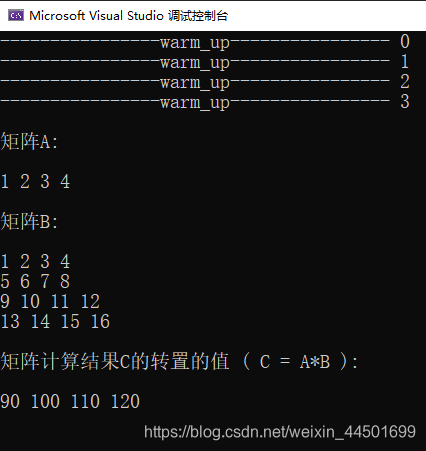
注意
报错:
On entry to GEMM_EX parameter 12 had a illegal value
原因是:这个函数的 lda, ldb 参数(主维度)只能是 4 的整数倍。
整合一下前边出现的代码
template <typename T1, typename T2>
void cublas_kernel()
{
// 定义状态变量
cublasHandle_t handle;
cublasCreate(&handle);
cudaEventCreate(&start);
cudaEventCreate(&stop);
//存储于内存中的矩阵
T1* h_A, * h_B;
T2* h_C, * h_CC;
//在内存中开辟空间
cudaHostAlloc((void**)&h_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_CC, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
MatrixINIT<T1>(A_ROW, A_COL, h_A);
MatrixINIT<T1>(B_ROW, B_COL, h_B);
// 打印待测试的矩阵
#if defined(USE_FLOAT_T)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 1);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 1);
#elif defined(USE_FLOAT_N)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#elif defined(USE_DOUBLE_T)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#elif defined(USE_DOUBLE_N)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0);
#elif defined(USE_INT8_T)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0, 0, "char");
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0, 0, "char");
#elif defined(USE_INT8_N)
Matrixshow<T1>("A", A_ROW, A_COL, h_A, 0, 0, "char");
Matrixshow<T1>("B", B_ROW, B_COL, h_B, 0, 0, "char");
#endif
//存储于显存中的矩阵
T1* d_A, * d_B;
T2* d_C;
cudaMalloc((void**)&d_A, sizeof(T1) * A_ROW * A_COL);
cudaMalloc((void**)&d_B, sizeof(T1) * B_ROW * B_COL);
cudaMalloc((void**)&d_C, sizeof(T2) * A_ROW * B_COL);
/*
cudaHostAlloc((void**)&d_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
*/
//创建流对象,用于任务级(Grid)同步
cudaStream_t stream;
cudaStreamCreateWithFlags(&stream, cudaStreamNonBlocking);
cublasSetStream(handle, stream);
const T2 a = 1.0f, b = 0.0f;
//计时开始
TIMER_START(_X);
//cudaEventRecord(start, 0);
for (int i = 0; i < N ; i++)
{
//数据从Host端拷贝到Device端、 cubals方式
/*
cublasSetMatrix(A_ROW, A_COL, sizeof(*h_A), h_A, A_ROW, d_A, A_ROW);
cublasSetMatrix(B_ROW, B_COL, sizeof(*h_B), h_B, B_ROW, d_B, B_ROW);
*/
cublasSetMatrixAsync(A_ROW, A_COL, sizeof(*h_A), h_A, A_ROW, d_A, A_ROW, stream);
cublasSetMatrixAsync(B_ROW, B_COL, sizeof(*h_B), h_B, B_ROW, d_B, B_ROW, stream);
//数据从Host端拷贝到Device端、 传统方式
//cudaMemcpy(d_A, H_A, sizeof(T1) * A_ROW * A_COL, cudaMemcpyHostToDevice);
//cudaMemcpy(d_B, H_B, sizeof(T1) * B_ROW * B_COL, cudaMemcpyHostToDevice);
//单独计算核函数运算时间
cudaEventRecord(start, 0);
#if defined(USE_FLOAT_N)
cublasSgemm(
handle,
CUBLAS_OP_N, //矩阵A的属性参数,不转置,按列优先
CUBLAS_OP_N, //矩阵B的属性参数,不转置,按列优先
B_COL, //矩阵B^T、C^T的行数
A_ROW, //矩阵A^T、C^T的列数
B_ROW, //B^T的列数,A^T的行数,此处也可为A_COL,一样的
&a, //alpha的值
d_B, //左矩阵,为B^T
B_COL, //B^T的leading dimension,按列优先,则leading dimension为B^T的行数(B的列数)
d_A, //右矩阵,为A^T
A_COL, //A^T的leading dimension,按列优先,则leading dimension为A^T的行数(A的列数)
&b, //beta的值
d_C, //结果矩阵C
B_COL //C^T的leading dimension,C^T矩阵一定按列优先,则leading dimension为C^T的行数(C的列数)
);//此处的h_C是按列存储的C^T
#elif defined(USE_FLOAT_T)
cublasSgemm(
handle,
CUBLAS_OP_T, //矩阵A的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
CUBLAS_OP_T, //矩阵B的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
A_ROW, //矩阵A、C的行数
B_COL, //矩阵B、C的列数
A_COL, //A的列数,B的行数,此处也可为B_ROW一样的
&a, //alpha的值
d_A, //左矩阵,为A
A_COL, //A的leading dimension,按列优先,则leading dimension为(A^T的行数)A的列数
d_B, //右矩阵,为B
B_COL, //B的leading dimension,按列优先,则leading dimension为(B^T的行数)A的列数
&b, //beta的值
d_C, //结果矩阵C
A_ROW //C的leading dimension,C矩阵一定按列优先,则leading dimension为C的行数
);//此处的h_C是按列存储的C
#elif defined(USE_DOUBLE_N)
cublasDgemm(
handle,
CUBLAS_OP_N, //矩阵A的属性参数,不转置,按列优先
CUBLAS_OP_N, //矩阵B的属性参数,不转置,按列优先
B_COL, //矩阵B^T、C^T的行数
A_ROW, //矩阵A^T、C^T的列数
B_ROW, //B^T的列数,A^T的行数,此处也可为A_COL,一样的
&a, //alpha的值
d_B, //左矩阵,为B^T
B_COL, //B^T的leading dimension,按列优先,则leading dimension为B^T的行数(B的列数)
d_A, //右矩阵,为A^T
A_COL, //A^T的leading dimension,按列优先,则leading dimension为A^T的行数(A的列数)
&b, //beta的值
d_C, //结果矩阵C
B_COL //C^T的leading dimension,C^T矩阵一定按列优先,则leading dimension为C^T的行数(C的列数)
);//此处的h_C是按列存储的C^T
#elif defined(USE_DOUBLE_T)
cublasDgemm(
handle,
CUBLAS_OP_T, //矩阵A的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
CUBLAS_OP_T, //矩阵B的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
A_ROW, //矩阵A、C的行数
B_COL, //矩阵B、C的列数
A_COL, //A的列数,B的行数,此处也可为B_ROW一样的
&a, //alpha的值
d_A, //左矩阵,为A
A_COL, //A的leading dimension,按列优先,则leading dimension为(A^T的行数)A的列数
d_B, //右矩阵,为B
B_COL, //B的leading dimension,按列优先,则leading dimension为(B^T的行数)A的列数
&b, //beta的值
d_C, //结果矩阵C
A_ROW //C的leading dimension,C矩阵一定按列优先,则leading dimension为C的行数
);//此处的h_C是按列存储的C
#elif defined(USE_INT8_N)
cublasGemmEx(handle, //句柄
CUBLAS_OP_N, //矩阵A的属性参数,不转置,按列优先
CUBLAS_OP_N, //矩阵B的属性参数,不转置,按列优先
B_COL, //矩阵B^T、C^T的行数
A_ROW, //矩阵A^T、C^T的列数
B_ROW, //B^T的列数,A^T的行数,此处也可为A_COL,一样的
&a, //alpha的值
d_B, //左矩阵,为B^T
CUDA_R_8I, //A矩阵计算模式,int8型
B_COL, //B^T的leading dimension,按列优先,则leading dimension为B^T的行数(B的列数)
d_A, //右矩阵,为A^T
CUDA_R_8I, //B矩阵计算模式,int8型
A_COL, //A^T的leading dimension,按列优先,则leading dimension为A^T的行数(A的列数)
&b, //乘法因子beta
d_C, //C结果矩阵
CUDA_R_32I, //C矩阵计算模式,int32型
B_COL, //C^T的leading dimension,C^T矩阵一定按列优先,则leading dimension为C^T的行数(C的列数)
CUDA_R_32I, //计算模式,int32模式
//CUBLAS_GEMM_ALGO0 //算法参数
CUBLAS_GEMM_DFALT
); //此处的h_C是按列存储的C^T
#elif defined(USE_INT8_T)
cublasGemmEx(handle, //句柄
CUBLAS_OP_T, //矩阵A的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
CUBLAS_OP_T, //矩阵B的属性参数,还是按列优先读取,但是在计算前,转置,变成正常c/c++的方式
A_ROW, //矩阵A、C的行数
B_COL, //矩阵B、C的列数
A_COL, //A的列数,B的行数,此处也可为B_ROW一样的
&a, //运算式的 α 值
d_A, //A矩阵
CUDA_R_8I, //A矩阵计算模式,int8型
A_COL, //A的leading dimension,按行优先存储,读取还是列优先,则leading dimension为(A^T的行数)A的列数
d_B, //B矩阵
CUDA_R_8I, //B矩阵计算模式,int8型
B_COL, //B的leading dimension,按行优先存储,读取还是列优先,则leading dimension为(B^T的行数)A的列数
&b, //乘法因子beta
d_C, //C结果矩阵
CUDA_R_32I, //C矩阵计算模式,int32型
A_ROW, //C的leading dimension,C矩阵一定按列优先,则leading dimension为C的行数
CUDA_R_32I, //计算模式,int32模式
//CUBLAS_GEMM_ALGO2 //算法参数
CUBLAS_GEMM_DFALT
); //此处的h_C是按列存储的C
#endif
//计时结束
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime, start, stop);
//TIMER_STOP(_X);
//cout << "GPU耗费了: " << TIMER_MSEC(_X) << " ms " << "\n";
//
//将Device端计算完的结果传输会Host端 cublas方式
//cublasGetMatrix(A_ROW, B_COL, sizeof(*h_C), d_C, A_ROW, h_C, A_ROW);
cublasGetMatrixAsync(A_ROW, B_COL, sizeof(*h_C), d_C, A_ROW, h_C, A_ROW, stream);
//传统方式
//cudaMemcpy(H_C, d_C, sizeof(T2) * A_ROW * B_COL, cudaMemcpyDeviceToHost);
}
TIMER_STOP(_X);
/*
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime_cublas, start, stop);
*/
//打印结果
//cout << "cublas_kernel GPU传输、计算花费了: " << TIMER_MSEC(_X) << " ms " << "\n";
//std::cout<< "GPU传输、计算花费了:" << elapsedTime_cublas << " ms" << std::endl;
//std::cout << "cublas_kernel GPU计算花费了:" << elapsedTime * N<< " ms" << std::endl<< std::endl;
#if defined(USE_FLOAT_T)
// 按行优先顺序读取h_C相当于做了CT的结果
Matrixshow<T2>("计算结果C的转置的值 ( C = A*B )", A_ROW, B_COL, h_C, 0, 1);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 1);
#endif
#elif defined(USE_FLOAT_N)
//按行读取h_C相当于做了CTT=C的结果
Matrixshow<T2>("计算结果C的值 ( C^T = (B^T*A^T) = (B*A)^T )", A_ROW, B_COL, h_C, 0, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 0);
#endif
#elif defined(USE_DOUBLE_T)
// 按行优先顺序读取h_C相当于做了CT的结果
Matrixshow<T2>("计算结果C的转置的值 ( C = A*B )", A_ROW, B_COL, h_C, 0, 1);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 1);
#endif
#elif defined(USE_DOUBLE_N)
//按行读取h_C相当于做了CTT=C的结果
Matrixshow<T2>("计算结果C的值 ( C^T = (B^T*A^T) = (B*A)^T )", A_ROW, B_COL, h_C, 0, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 0);
#endif
#elif defined(USE_INT8_T)
// 按行优先顺序读取h_C相当于做了CT的结果
Matrixshow<T2>("计算结果C的转置的值 ( C = A*B )", A_ROW, B_COL, h_C, 0, 1);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 1);
#endif
#elif defined(USE_INT8_N)
//按行读取h_C相当于做了CTT=C的结果
//Matrixshow<T2>("计算结果C的值 ( C^T = (B^T*A^T) = (B*A)^T )", A_ROW, B_COL, h_C, 0, 0);
cout << endl;
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 0);
#endif
#endif
//释放内存
cudaFree(d_A);
cudaFree(d_B);
cudaFree(d_C);
/*
cudaFreeHost(d_A);
cudaFreeHost(d_B);
cudaFreeHost(d_C);
*/
cudaFreeHost(h_A);
cudaFreeHost(h_B);
cudaFreeHost(h_C);
cudaFreeHost(h_CC);
cublasDestroy(handle);
cudaEventDestroy(start);
cudaEventDestroy(stop);
cudaStreamDestroy(stream);
}
ISPC的矩阵代码
ISPC的一些简单介绍和配置和使用请参考之前记录的ISPC的专栏文章。
下面的代码是根据ISPC提供的参考代码修改的。
这个好像不支持c++的模板函数,所以写起来感觉可能很多。
SGEMM_kernels_ispc.ispc
// Various ISPC SGEMM kernel and task/kernel implementations
// Junkins, September 2018
#define TILE_SIZE 32
export uniform int SGEMM_get_program_count() {
return programCount;
}
export uniform int SGEMM_get_tile_size() {
return TILE_SIZE;
}
// This version is modified version of 'SGEMM_tileNoSIMDIntrin'.
// The tile used to read/write values for re-use is a 2D block of height 2 instead of a n array of same width.
#define TILE_HEIGHT 2
#define TILE_WIDTH 32
// This version is a further modified version of 'SGEMM_tileBlockNoSIMDIntrin'.
// Since we already know the tile height, the loop used to access the tile vertically is replaced.
export void SGEMM_tileBlockNoSIMDIntrin_2_int(uniform int matrixA[], uniform int matrixB[], uniform int matrixC[],
uniform int M, uniform int N, uniform int K) {
uniform int sumTile[TILE_HEIGHT][TILE_WIDTH];
uniform int oneAVal[TILE_HEIGHT];
for (uniform unsigned int m = 0; m < M; m += TILE_HEIGHT) {
for (uniform unsigned int k0 = 0; k0 < K; k0 += TILE_WIDTH) {
// SPMD "horizontally" over TILE dimension.
foreach (ki = 0 ... TILE_WIDTH) {
// No scatter required.
sumTile[0][ki] = 0;
sumTile[1][ki] = 0;
}
// Loop over the the matrix N dimension:
for (uniform unsigned int n = 0; n < N; n++) {
uniform unsigned int mTimesNPlusN = (m + 0)*N + n;
uniform unsigned int mPlusOneTimesNPlusN = (m + 1)*N + n;
prefetch_nt(&matrixA[mPlusOneTimesNPlusN]);
prefetch_nt(&matrixA[mTimesNPlusN]);
oneAVal[0] = matrixA[mTimesNPlusN];
oneAVal[1] = matrixA[mPlusOneTimesNPlusN];
uniform unsigned int nTimesKPlusk0 = n*K + k0;
// SPMD iterate over the TILE dimension, but within for loop nest:
foreach (kt = 0 ... TILE_WIDTH) {
// Note, no gather required.
varying int matB1 = matrixB[nTimesKPlusk0 + kt];
// Pure SIMD FMAC:
sumTile[0][kt] += oneAVal[0] * matB1;
sumTile[1][kt] += oneAVal[1] * matB1;
}
}
uniform unsigned int mTimesKPlusK0 = (m + 0)*K + k0;
uniform unsigned int mPlusOneTimesKPlusK0 = (m + 1)*K + k0;
// SPMD "horizontally" again over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
matrixC[mTimesKPlusK0 + ki] = sumTile[0][ki];
matrixC[mPlusOneTimesKPlusK0 + ki] = sumTile[1][ki];
}
}
}
}
// Multiple task version of the above:
task void SGEMM_tileBlockNoSIMDIntrin_2_task_int(uniform int matrixA[], uniform int matrixB[], uniform int matrixC[],
uniform int M, uniform int N, uniform int K) {
uniform int sumTile[TILE_HEIGHT][TILE_WIDTH];
uniform int oneAVal[TILE_HEIGHT];
// Determine workset for this task instance:
uniform unsigned int uNumRowsPerTask = M / taskCount;
uniform unsigned int uRowStart = uNumRowsPerTask * taskIndex;
uniform unsigned int uRowEnd = uRowStart + uNumRowsPerTask;
for (uniform unsigned int m = uRowStart; m < uRowEnd; m += TILE_HEIGHT) {
for (uniform unsigned int k0 = 0; k0 < K; k0 += TILE_WIDTH) {
// SPMD "horizontally" over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
// No scatter required.
sumTile[0][ki] = 0;
sumTile[1][ki] = 0;
}
// Loop over the the matrix N dimension:
for (uniform unsigned int n = 0; n < N; n++) {
uniform unsigned int mTimesNPlusN = (m + 0)*N + n;
uniform unsigned int mPlusOneTimesNPlusN = (m + 1)*N + n;
prefetch_nt(&matrixA[mPlusOneTimesNPlusN]);
prefetch_nt(&matrixA[mTimesNPlusN]);
oneAVal[0] = matrixA[mTimesNPlusN];
oneAVal[1] = matrixA[mPlusOneTimesNPlusN];
uniform unsigned int nTimesKPlusk0 = n*K + k0;
// SPMD iterate over the TILE dimension, but within for loop nest:
foreach (kt = 0 ... TILE_WIDTH) {
// Note, no gather required.
varying int matB1 = matrixB[nTimesKPlusk0 + kt];
// Pure SIMD FMAC:
sumTile[0][kt] += oneAVal[0] * matB1;
sumTile[1][kt] += oneAVal[1] * matB1;
}
}
uniform unsigned int mTimesKPlusK0 = (m + 0)*K + k0;
uniform unsigned int mPlusOneTimesKPlusK0 = (m + 1)*K + k0;
// SPMD "horizontally" again over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
matrixC[mTimesKPlusK0 + ki] = sumTile[0][ki];
matrixC[mPlusOneTimesKPlusK0 + ki] = sumTile[1][ki];
}
}
}
}
export void SGEMM_tileBlockNoSIMDIntrin_2_withTasks_int(uniform int matA[], uniform int matB[], uniform int matC[],
uniform int M, uniform int N, uniform int K) {
// The algorithm divides rows in matrix C (M size) between tasks.
// We want each task to process programCount rows in C matrix to maximize SIMD usage.
uniform int numTasks = M / programCount;
launch[numTasks] SGEMM_tileBlockNoSIMDIntrin_2_task_int(matA, matB, matC, M, N, K);
}
// This version is a further modified version of 'SGEMM_tileBlockNoSIMDIntrin'.
// Since we already know the tile height, the loop used to access the tile vertically is replaced.
export void SGEMM_tileBlockNoSIMDIntrin_2_float(uniform float matrixA[], uniform float matrixB[], uniform float matrixC[],
uniform int M, uniform int N, uniform int K) {
uniform float sumTile[TILE_HEIGHT][TILE_WIDTH];
uniform float oneAVal[TILE_HEIGHT];
for (uniform unsigned int m = 0; m < M; m += TILE_HEIGHT) {
for (uniform unsigned int k0 = 0; k0 < K; k0 += TILE_WIDTH) {
// SPMD "horizontally" over TILE dimension.
foreach (ki = 0 ... TILE_WIDTH) {
// No scatter required.
sumTile[0][ki] = 0.0f;
sumTile[1][ki] = 0.0f;
}
// Loop over the the matrix N dimension:
for (uniform unsigned int n = 0; n < N; n++) {
uniform unsigned int mTimesNPlusN = (m + 0)*N + n;
uniform unsigned int mPlusOneTimesNPlusN = (m + 1)*N + n;
prefetch_nt(&matrixA[mPlusOneTimesNPlusN]);
prefetch_nt(&matrixA[mTimesNPlusN]);
oneAVal[0] = matrixA[mTimesNPlusN];
oneAVal[1] = matrixA[mPlusOneTimesNPlusN];
uniform unsigned int nTimesKPlusk0 = n*K + k0;
// SPMD iterate over the TILE dimension, but within for loop nest:
foreach (kt = 0 ... TILE_WIDTH) {
// Note, no gather required.
varying float matB1 = matrixB[nTimesKPlusk0 + kt];
// Pure SIMD FMAC:
sumTile[0][kt] += oneAVal[0] * matB1;
sumTile[1][kt] += oneAVal[1] * matB1;
}
}
uniform unsigned int mTimesKPlusK0 = (m + 0)*K + k0;
uniform unsigned int mPlusOneTimesKPlusK0 = (m + 1)*K + k0;
// SPMD "horizontally" again over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
matrixC[mTimesKPlusK0 + ki] = sumTile[0][ki];
matrixC[mPlusOneTimesKPlusK0 + ki] = sumTile[1][ki];
}
}
}
}
// Multiple task version of the above:
task void SGEMM_tileBlockNoSIMDIntrin_2_task_float(uniform float matrixA[], uniform float matrixB[], uniform float matrixC[],
uniform int M, uniform int N, uniform int K) {
uniform float sumTile[TILE_HEIGHT][TILE_WIDTH];
uniform float oneAVal[TILE_HEIGHT];
// Determine workset for this task instance:
uniform unsigned int uNumRowsPerTask = M / taskCount;
uniform unsigned int uRowStart = uNumRowsPerTask * taskIndex;
uniform unsigned int uRowEnd = uRowStart + uNumRowsPerTask;
for (uniform unsigned int m = uRowStart; m < uRowEnd; m += TILE_HEIGHT) {
for (uniform unsigned int k0 = 0; k0 < K; k0 += TILE_WIDTH) {
// SPMD "horizontally" over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
// No scatter required.
sumTile[0][ki] = 0.0f;
sumTile[1][ki] = 0.0f;
}
// Loop over the the matrix N dimension:
for (uniform unsigned int n = 0; n < N; n++) {
uniform unsigned int mTimesNPlusN = (m + 0)*N + n;
uniform unsigned int mPlusOneTimesNPlusN = (m + 1)*N + n;
prefetch_nt(&matrixA[mPlusOneTimesNPlusN]);
prefetch_nt(&matrixA[mTimesNPlusN]);
oneAVal[0] = matrixA[mTimesNPlusN];
oneAVal[1] = matrixA[mPlusOneTimesNPlusN];
uniform unsigned int nTimesKPlusk0 = n*K + k0;
// SPMD iterate over the TILE dimension, but within for loop nest:
foreach (kt = 0 ... TILE_WIDTH) {
// Note, no gather required.
varying float matB1 = matrixB[nTimesKPlusk0 + kt];
// Pure SIMD FMAC:
sumTile[0][kt] += oneAVal[0] * matB1;
sumTile[1][kt] += oneAVal[1] * matB1;
}
}
uniform unsigned int mTimesKPlusK0 = (m + 0)*K + k0;
uniform unsigned int mPlusOneTimesKPlusK0 = (m + 1)*K + k0;
// SPMD "horizontally" again over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
matrixC[mTimesKPlusK0 + ki] = sumTile[0][ki];
matrixC[mPlusOneTimesKPlusK0 + ki] = sumTile[1][ki];
}
}
}
}
export void SGEMM_tileBlockNoSIMDIntrin_2_withTasks_float(uniform float matA[], uniform float matB[], uniform float matC[],
uniform int M, uniform int N, uniform int K) {
// The algorithm divides rows in matrix C (M size) between tasks.
// We want each task to process programCount rows in C matrix to maximize SIMD usage.
uniform int numTasks = M / programCount;
launch[numTasks] SGEMM_tileBlockNoSIMDIntrin_2_task_float(matA, matB, matC, M, N, K);
}
// This version is a further modified version of 'SGEMM_tileBlockNoSIMDIntrin'.
// Since we already know the tile height, the loop used to access the tile vertically is replaced.
export void SGEMM_tileBlockNoSIMDIntrin_2_double(uniform double matrixA[], uniform double matrixB[], uniform double matrixC[],
uniform int M, uniform int N, uniform int K) {
uniform double sumTile[TILE_HEIGHT][TILE_WIDTH];
uniform double oneAVal[TILE_HEIGHT];
for (uniform unsigned int m = 0; m < M; m += TILE_HEIGHT) {
for (uniform unsigned int k0 = 0; k0 < K; k0 += TILE_WIDTH) {
// SPMD "horizontally" over TILE dimension.
foreach (ki = 0 ... TILE_WIDTH) {
// No scatter required.
sumTile[0][ki] = 0.0d;
sumTile[1][ki] = 0.0d;
}
// Loop over the the matrix N dimension:
for (uniform unsigned int n = 0; n < N; n++) {
uniform unsigned int mTimesNPlusN = (m + 0)*N + n;
uniform unsigned int mPlusOneTimesNPlusN = (m + 1)*N + n;
prefetch_nt(&matrixA[mPlusOneTimesNPlusN]);
prefetch_nt(&matrixA[mTimesNPlusN]);
oneAVal[0] = matrixA[mTimesNPlusN];
oneAVal[1] = matrixA[mPlusOneTimesNPlusN];
uniform unsigned int nTimesKPlusk0 = n*K + k0;
// SPMD iterate over the TILE dimension, but within for loop nest:
foreach (kt = 0 ... TILE_WIDTH) {
// Note, no gather required.
varying double matB1 = matrixB[nTimesKPlusk0 + kt];
// Pure SIMD FMAC:
sumTile[0][kt] += oneAVal[0] * matB1;
sumTile[1][kt] += oneAVal[1] * matB1;
}
}
uniform unsigned int mTimesKPlusK0 = (m + 0)*K + k0;
uniform unsigned int mPlusOneTimesKPlusK0 = (m + 1)*K + k0;
// SPMD "horizontally" again over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
matrixC[mTimesKPlusK0 + ki] = sumTile[0][ki];
matrixC[mPlusOneTimesKPlusK0 + ki] = sumTile[1][ki];
}
}
}
}
// Multiple task version of the above:
task void SGEMM_tileBlockNoSIMDIntrin_2_task_double(uniform double matrixA[], uniform double matrixB[], uniform double matrixC[],
uniform int M, uniform int N, uniform int K) {
uniform double sumTile[TILE_HEIGHT][TILE_WIDTH];
uniform double oneAVal[TILE_HEIGHT];
// Determine workset for this task instance:
uniform unsigned int uNumRowsPerTask = M / taskCount;
uniform unsigned int uRowStart = uNumRowsPerTask * taskIndex;
uniform unsigned int uRowEnd = uRowStart + uNumRowsPerTask;
for (uniform unsigned int m = uRowStart; m < uRowEnd; m += TILE_HEIGHT) {
for (uniform unsigned int k0 = 0; k0 < K; k0 += TILE_WIDTH) {
// SPMD "horizontally" over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
// No scatter required.
sumTile[0][ki] = 0.0d;
sumTile[1][ki] = 0.0d;
}
// Loop over the the matrix N dimension:
for (uniform unsigned int n = 0; n < N; n++) {
uniform unsigned int mTimesNPlusN = (m + 0)*N + n;
uniform unsigned int mPlusOneTimesNPlusN = (m + 1)*N + n;
prefetch_nt(&matrixA[mPlusOneTimesNPlusN]);
prefetch_nt(&matrixA[mTimesNPlusN]);
oneAVal[0] = matrixA[mTimesNPlusN];
oneAVal[1] = matrixA[mPlusOneTimesNPlusN];
uniform unsigned int nTimesKPlusk0 = n*K + k0;
// SPMD iterate over the TILE dimension, but within for loop nest:
foreach (kt = 0 ... TILE_WIDTH) {
// Note, no gather required.
varying double matB1 = matrixB[nTimesKPlusk0 + kt];
// Pure SIMD FMAC:
sumTile[0][kt] += oneAVal[0] * matB1;
sumTile[1][kt] += oneAVal[1] * matB1;
}
}
uniform unsigned int mTimesKPlusK0 = (m + 0)*K + k0;
uniform unsigned int mPlusOneTimesKPlusK0 = (m + 1)*K + k0;
// SPMD "horizontally" again over TILE dimension:
foreach (ki = 0 ... TILE_WIDTH) {
matrixC[mTimesKPlusK0 + ki] = sumTile[0][ki];
matrixC[mPlusOneTimesKPlusK0 + ki] = sumTile[1][ki];
}
}
}
}
export void SGEMM_tileBlockNoSIMDIntrin_2_withTasks_double(uniform double matA[], uniform double matB[], uniform double matC[],
uniform int M, uniform int N, uniform int K) {
// The algorithm divides rows in matrix C (M size) between tasks.
// We want each task to process programCount rows in C matrix to maximize SIMD usage.
uniform int numTasks = M / programCount;
launch[numTasks] SGEMM_tileBlockNoSIMDIntrin_2_task_double(matA, matB, matC, M, N, K);
}
ispc.hpp
#include <device_launch_parameters.h>
#include "cuda_runtime.h"
#include "cublas_v2.h"
#include <iostream>
#include <stdlib.h>
#include <math.h>
#include "SGEMM_kernels_ispc.h"
#include "matrix.hpp"
bool tasks;
using namespace std;
using namespace ispc;
typedef void (*SGEMMFuncPtr)(void);
typedef void (*SGEMMFuncPtr_SingleThreaded_int)(int* matrixA, int* matrixB, int* matrixC, unsigned int A_ROW, unsigned int A_COL, unsigned int B_COL);
typedef void (*SGEMMFuncPtr_MultiThreaded_int)(int* matrixA, int* matrixB, int* matrixC, unsigned int A_ROW, unsigned int A_COL, unsigned int B_COL);
typedef void (*SGEMMFuncPtr_SingleThreaded_float)(float* matrixA, float* matrixB, float* matrixC, unsigned int A_ROW, unsigned int A_COL, unsigned int B_COL);
typedef void (*SGEMMFuncPtr_MultiThreaded_float)(float* matrixA, float* matrixB, float* matrixC, unsigned int A_ROW, unsigned int A_COL, unsigned int B_COL);
typedef void (*SGEMMFuncPtr_SingleThreaded_double)(double* matrixA, double* matrixB, double* matrixC, unsigned int A_ROW, unsigned int A_COL, unsigned int B_COL);
typedef void (*SGEMMFuncPtr_MultiThreaded_double)(double* matrixA, double* matrixB, double* matrixC, unsigned int A_ROW, unsigned int A_COL, unsigned int B_COL);
template <typename T1>
void Test_SGEMM(SGEMMFuncPtr SGEMMFunc, T1* matrixA, T1* matrixB, T1* matrixC,
unsigned int A_ROW, unsigned int A_COL, unsigned int B_COL, bool task) {
unsigned int i;
if (task) {
// type cast
#if defined(USE_ISPC_INT)
auto SGEMMFunc_MT = (SGEMMFuncPtr_MultiThreaded_int)SGEMMFunc;
#elif defined(USE_ISPC_FLOAT)
auto SGEMMFunc_MT = (SGEMMFuncPtr_MultiThreaded_float)SGEMMFunc;
#elif defined(USE_ISPC_DOUBLE)
auto SGEMMFunc_MT = (SGEMMFuncPtr_MultiThreaded_double)SGEMMFunc;
#endif
for (i = 0; i < N; i++) {
SGEMMFunc_MT(matrixA, matrixB, matrixC, A_ROW, A_COL, B_COL);
}
}
else {
// type cast
#if defined(USE_ISPC_INT)
auto SGEMMFunc_ST = (SGEMMFuncPtr_SingleThreaded_int)SGEMMFunc;
#elif defined(USE_ISPC_FLOAT)
auto SGEMMFunc_ST = (SGEMMFuncPtr_SingleThreaded_float)SGEMMFunc;
#elif defined(USE_ISPC_DOUBLE)
auto SGEMMFunc_ST = (SGEMMFuncPtr_SingleThreaded_double)SGEMMFunc;
#endif
for (i = 0; i < N; i++)
{
SGEMMFunc_ST(matrixA, matrixB, matrixC, A_ROW, A_COL, B_COL);
}
}
}
template <typename T1, typename T2>
void cpu_ispc() {
int programCount = SGEMM_get_program_count();
int tileSize = SGEMM_get_tile_size();
if (B_COL % programCount != 0 || B_COL % tileSize != 0) {
printf("\nNumber of columns in Matrix B (K) must be a multiple of %d (target width) and %d (tile size)!\n",
programCount, tileSize);
exit(-1);
}
if (A_ROW % programCount != 0) {
printf("\nNumber of rows in Matrix A (M) must be a multiple of %d (target width)!\n", programCount);
exit(-1);
}
if (A_COL % programCount != 0) {
printf("\nNumber of columns in Matrix A (N), which is also number of rows in Matrix B, "
"must be a multiple of %d (target width)!\n",
programCount);
exit(-1);
}
T1* h_A, * h_B;
T2* h_C, * h_CC;
h_A = (T1*)malloc(sizeof(T1) * A_ROW * A_COL);
h_B = (T1*)malloc(sizeof(T1) * B_ROW * B_COL);
h_C = (T2*)malloc(sizeof(T2) * A_ROW * B_COL);
h_CC = (T2*)malloc(sizeof(T2) * A_ROW * B_COL);
/*
cudaHostAlloc((void**)&h_A, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_B, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_C, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_CC, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
*/
//初始化矩阵
MatrixINIT<T1>(A_ROW, A_COL, h_A);
MatrixINIT<T1>(B_ROW, B_COL, h_B);
//打印矩阵
//Matrixshow<T1>("A", A_ROW, A_COL, h_A, 1);
//Matrixshow<T1>("B", B_ROW, B_COL, h_B, 1);
// Single threaded test cases:
tasks = false;
TIMER_START(t);
#if defined(USE_ISPC_INT)
Test_SGEMM<T1>((SGEMMFuncPtr)SGEMM_tileBlockNoSIMDIntrin_2_int, h_A, h_B,
h_C, A_ROW, A_COL, B_COL, tasks);
#elif defined(USE_ISPC_FLOAT)
Test_SGEMM<T1>((SGEMMFuncPtr)SGEMM_tileBlockNoSIMDIntrin_2_float, h_A, h_B,
h_C, A_ROW, A_COL, B_COL, tasks);
#elif defined(USE_ISPC_DOUBLE)
Test_SGEMM<T1>((SGEMMFuncPtr)SGEMM_tileBlockNoSIMDIntrin_2_double, h_A, h_B,
h_C, A_ROW, A_COL, B_COL, tasks);
#endif
TIMER_STOP(t);
cout << "ISPC单任务花费了:" << TIMER_MSEC(t) << " ms " << endl << endl;
cout << endl;
//打印结果
//Matrixshow<T2>("ISPC 计算结果C的值:", A_ROW, B_COL, h_C, 1,0);
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 0);
#endif
// Multi-threaded test cases:
tasks = true;
TIMER_START(X);
#if defined(USE_ISPC_INT)
Test_SGEMM<T1>((SGEMMFuncPtr)SGEMM_tileBlockNoSIMDIntrin_2_withTasks_int,
h_A, h_B, h_C, A_ROW, A_COL, B_COL, tasks);
#elif defined(USE_ISPC_FLOAT)
Test_SGEMM<T1>((SGEMMFuncPtr)SGEMM_tileBlockNoSIMDIntrin_2_withTasks_float,
h_A, h_B, h_C, A_ROW, A_COL, B_COL, tasks);
#elif defined(USE_ISPC_DOUBLE)
Test_SGEMM<T1>((SGEMMFuncPtr)SGEMM_tileBlockNoSIMDIntrin_2_withTasks_double,
h_A, h_B, h_C, A_ROW, A_COL, B_COL, tasks);
#endif
TIMER_STOP(X);
cout << "ISPC多任务花费了:" << TIMER_MSEC(X) << " ms " << endl << endl;
cout << endl;
//打印结果
//Matrixshow<T2>("ISPC 计算结果C的值:", A_ROW, B_COL, h_C, 1, 0);
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_A, h_B, A_ROW, A_COL, B_COL, h_C, h_CC, 0);
#endif
free(h_A);
free(h_B);
free(h_C);
free(h_CC);
/*
cudaFreeHost(h_A);
cudaFreeHost(h_B);
cudaFreeHost(h_C);
cudaFreeHost(h_CC);
*/
}
自己写的cuda矩阵计算核函数
使用了共享内存进行优化,一些优化的介绍查看之前记录的cuda。
template <typename T1, typename T2>
__global__ void MatrixMulCUDA(const T1* A, const T1 * B, T2* C,
const int ROW_A, const int COL_A, const int ROW_B, const int COL_B)
{
int tx = threadIdx.x;
int ty = threadIdx.y;
//当前线程对应的矩阵C的元素位置
int row = blockIdx.y * BLOCK_SIZE + ty;
int col = blockIdx.x * BLOCK_SIZE + tx;
//int I = (COL_A + BLOCK_SIZE - 1) / BLOCK_SIZE;
int I = (COL_A + BLOCK_SIZE - 1) / BLOCK_SIZE;
T2 t=0.0f, Csub = 0.0f, comp = 0.0f;
//避免bankconflict
__shared__ float As[BLOCK_SIZE+1][BLOCK_SIZE+1];
__shared__ float Bs[BLOCK_SIZE+1][BLOCK_SIZE+1];
//每个Block都将遍历A的一整行块和B的一整列块
//每个线程主要负责一行和一列的内积,另外还负责为当前循环中所计算的块填充一个元素到共享内存中
//快速向上取整
for (int i = 0; i < I; i++) {
if (row < ROW_A && i * BLOCK_SIZE + tx < COL_A)
As[ty][tx] = A[row * COL_A + i * BLOCK_SIZE + tx];//所有计算单元同时加载,所以下面的for循环中As和Bs都已配置完成
else
As[ty][tx] = 0;
if (col < COL_B && i * BLOCK_SIZE + ty < ROW_B)
Bs[ty][tx] = B[(i * BLOCK_SIZE + ty) * COL_B + col];
else
Bs[ty][tx] = 0;
//让同一块中的不同线程指令流同步,保证共享内存中矩阵块的元素全部加载
__syncthreads();//各线程执行到此函数时等待,直到全部线程同步
//Kahan's Summation Formula
//虽然外层循环是面向Block的,但这里内层循环只计算了两块中某行和某列的
for (int j = 0; j < BLOCK_SIZE; ++j)
{
// c += As[ty][j] * Bs[j][tx];
comp -= As[ty][j] * Bs[j][tx];
t = Csub - comp;
comp = (t - Csub) + comp;
Csub = t;
}
__syncthreads();
}
if (row < ROW_A && col < COL_B)
{
C[row * COL_B + col] = Csub;
}
}
template <typename T1, typename T2>
void My_kernel()
{
cudaEventCreate(&start);
cudaEventCreate(&stop);
//分配CPU上的存储空间
T1* h_a, * h_b, * h_c, * h_cc;
cudaHostAlloc((void**)&h_a, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_b, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_c, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&h_cc, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
MatrixINIT<T1>(A_ROW, A_COL, h_a);
MatrixINIT<T1>(B_ROW, B_COL, h_b);
/*
Matrixshow<T1>("A", A_ROW, A_COL, h_a, 0);
Matrixshow<T1>("B", B_ROW, B_COL, h_b, 0);
*/
//分配GPU上的存储空间
T1* d_a, * d_b;
T2* d_c;
/*
cudaHostAlloc((void**)&d_a, sizeof(T1) * A_ROW * A_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_b, sizeof(T1) * B_ROW * B_COL, cudaHostAllocDefault);
cudaHostAlloc((void**)&d_c, sizeof(T2) * A_ROW * B_COL, cudaHostAllocDefault);
*/
cudaMalloc((void**)&d_a, sizeof(T1) * A_ROW * A_COL);
cudaMalloc((void**)&d_b, sizeof(T1) * B_ROW * B_COL);
cudaMalloc((void**)&d_c, sizeof(T2) * A_ROW * B_COL);
unsigned int grid_rows = (A_ROW + BLOCK_SIZE - 1) / BLOCK_SIZE;
unsigned int grid_cols = (B_COL + BLOCK_SIZE - 1) / BLOCK_SIZE;
dim3 grid(grid_rows, grid_cols);
dim3 blocks(BLOCK_SIZE, BLOCK_SIZE);
//创建流对象,用于任务级(Grid)同步
cudaStream_t stream;
cudaStreamCreateWithFlags(&stream, cudaStreamNonBlocking);
//计时开始
TIMER_START(_X);
for (int i = 0; i < N; ++i)
{
// copy matrix A and B from host to device memory
cudaMemcpyAsync(d_a, h_a, sizeof(T1) * A_ROW * A_COL, cudaMemcpyHostToDevice, stream);
cudaMemcpyAsync(d_b, h_b, sizeof(T1) * B_ROW * B_COL, cudaMemcpyHostToDevice, stream);
//cudaMemcpy(d_a, h_a, sizeof(T1) * A_ROW * A_COL, cudaMemcpyHostToDevice);
//cudaMemcpy(d_b, h_b, sizeof(T1) * B_ROW * B_COL, cudaMemcpyHostToDevice);
cudaEventRecord(start, 0);
MatrixMulCUDA<T1, T2> << < grid, blocks >> > (d_a, d_b, d_c, A_ROW, A_COL, B_ROW, B_COL);
cudaDeviceSynchronize();
cudaEventRecord(stop, 0);
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime_mykernel, start, stop);
cudaMemcpyAsync(h_c, d_c, sizeof(T2) * A_ROW * B_COL, cudaMemcpyDeviceToHost, stream);
//cudaMemcpy(h_c, d_c, sizeof(T2) * A_ROW * B_COL, cudaMemcpyDeviceToHost);
}
TIMER_STOP(_X);
cout <<"mykernel GPU传输、计算花费了: " << TIMER_MSEC(_X) << " ms " << "\n";
std::cout <<"mykernel GPU计算花费了:"<<elapsedTime_mykernel * N<< " ms" << std::endl;
//Matrixshow<T2>("计算结果矩阵C的值", A_ROW, B_COL, h_c, 0);
cout << endl;
//检查计算是否正确
#if defined(USE_CPU_COST)
cpu_matrix_mult<T1, T2>(h_a, h_b, A_ROW, A_COL, B_COL, h_c, h_cc, 0);
#endif
//清理内存
cudaFree(d_a);
cudaFree(d_b);
cudaFree(d_b);
cudaFreeHost(h_a);
cudaFreeHost(h_b);
cudaFreeHost(h_c);
cudaFreeHost(h_cc);
cudaEventDestroy(start);
cudaEventDestroy(stop);
cudaStreamDestroy(stream);
}
性能对比平台
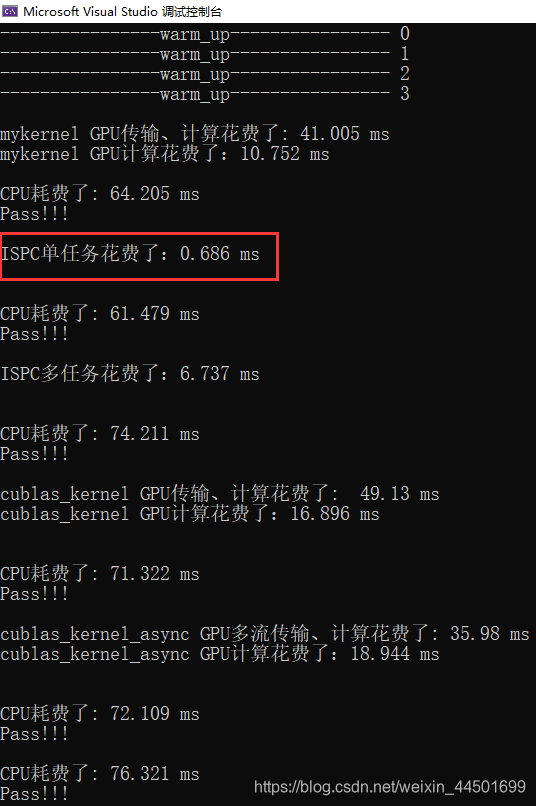
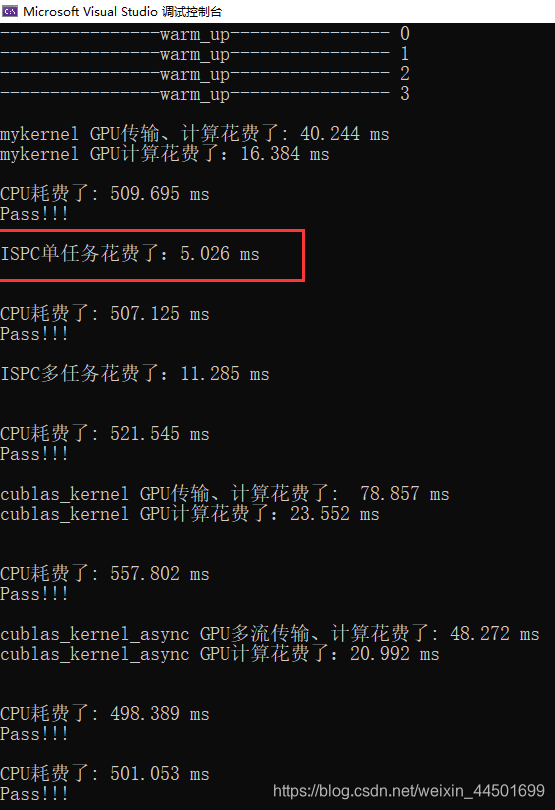
CPU 英特尔八代i7-8550U, GPU: NVIDIA GeForce MAX150; 均为500个epoch的测试,
FLAOT
32*32的矩阵:
64*64的矩阵:
128*128的矩阵:
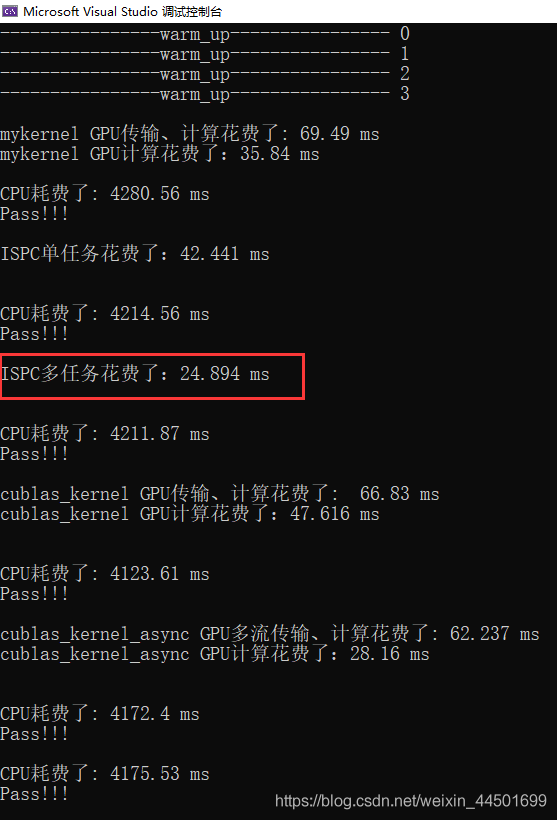
256*256的矩阵:
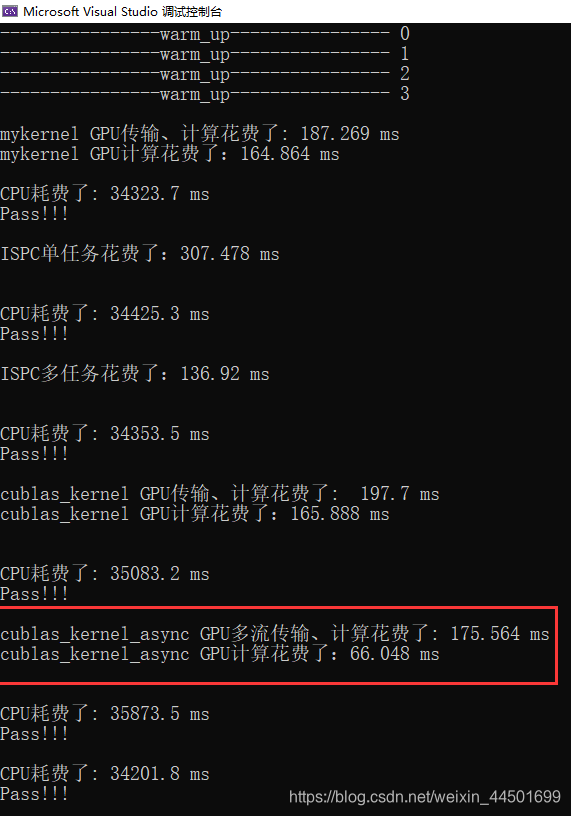
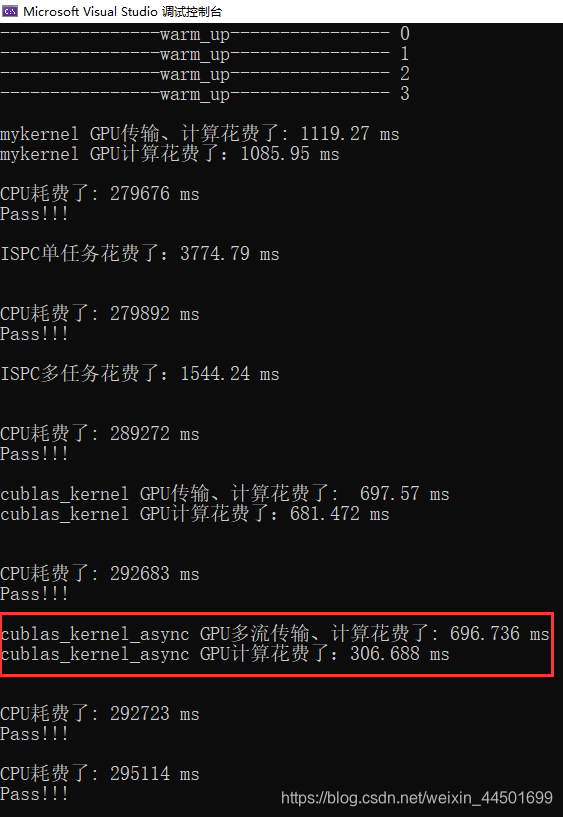
512*512 的矩阵:
小结
当矩阵正在64左右,ISPC单任务的代码是运行的最快的。当矩阵数量在64以上是ISPC的多任务快于单核,当矩阵达到256以上时,cublas的多流运行的最快。相比自己手撸的cuda函数运行速度和cublas的完全不是一个数量级的,优化之路还长啊。
INT8
512*512 的矩阵:
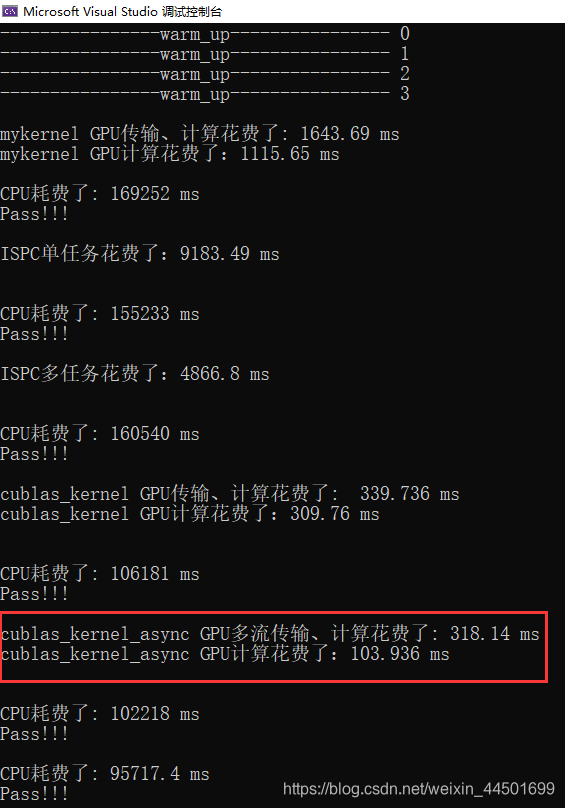
小结:
使用INT8计算时比FLOAT32的速度提升有三倍之多,没有达到理论的四倍速度比,受到带宽和其他一些资源调度的影响。不过已经快到飞起来。
其他注意事项
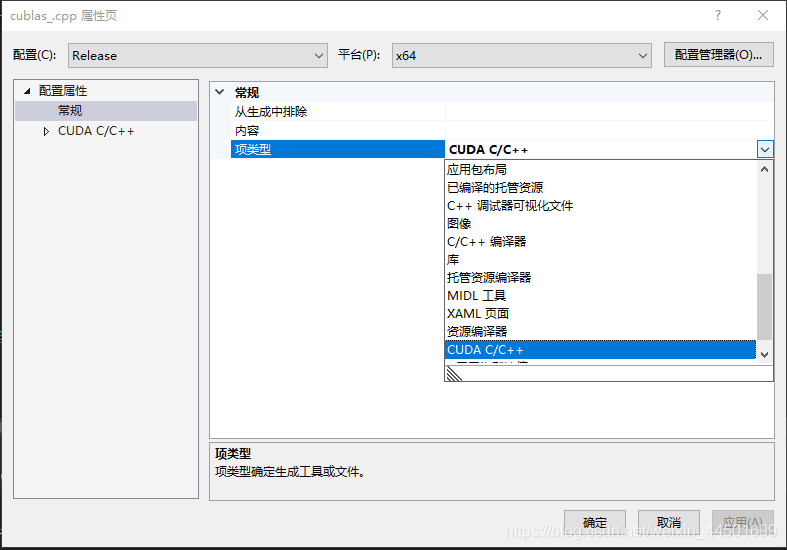
注意我这cublas_.cpp是CPP结尾的文件,不是cu结尾的文件,选中cublas_.cpp,然后点击右键配置属性,使用时记得把它改为 CUDA C/C++的。
更多(代码)
也不知道写点啥了,代码都有注释,有关更多的比较测试,读者们可自行尝试。
所有的资源代码已上传至github;