文章目录
(一)本文数据资料下载
python建模会持续更新,用途是只作为个人笔记。我博客中的所有资料都可通过我提供的链接永久获取,希望大家一起相互促进,相互努力。
本文所有代码、资料获取链接:
链接:https://pan.baidu.com/s/1ZGa_enCUxX7zvnUbxv_ICQ
提取码:p2bv
(二)简单介绍一下定义
插值:插值就是已知一组离散的数据点集,在集合内部某两个点之间预测函数值的方法。
拟合:已知有限个数据点,求近似函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最小。
详细了解可下载PPT:https://pan.baidu.com/s/149o1AzL3Iupf2MfXdbVO5Q
提取码:fq3o
(三)介绍我们可能用到的模块和代码(重点)
本章作用:为了能清晰的看懂本章的接下来的代码做铺垫。
3.1 scipy.interpolate 模块
scipy.interpolate 模块有一维插值函数(interp1d)、二位插值函数(interp2d)、多为插值函数(interpn、interpnd)。
内插法和外插法的区别:是处理方法不同、职责不同、工作内容不同,核心区别就是:内插法在样本数据的范围内预测,比外插法要准。用回归方程预测范围以外的数值称为外插法,而内插法是对数据范围内的点进行预测。
3.1.1 一维插值函数 (interp1d)
interp1d :用于固定已知的数据点。( interp1d 是内插法,不能用于外插值)。
interp1d(x, y, kind='linear', ...)
- x:已知的数据集的 x 值,为一维数组形式。
- y:已知数据集的 y 值,可以为多维数组形式(注意:y数组长度等于x数组长度。)
- kind:字符串或整数,可选项,指定使用的样条曲线的种类或插值方法。
| 候选值 | 作用 |
|---|---|
| ‘zero’ 、‘nearest’ | 阶梯插值,相当于0阶B样条曲线 |
| ‘slinear’ 、‘linear’ | 线性插值,用一条直线连接所有的取样点,相当于一阶B样条曲线 |
| ‘quadratic’、‘cubic’ | 二阶和三阶的线性插值,更高阶的曲线可以直接使用整数值指定 |
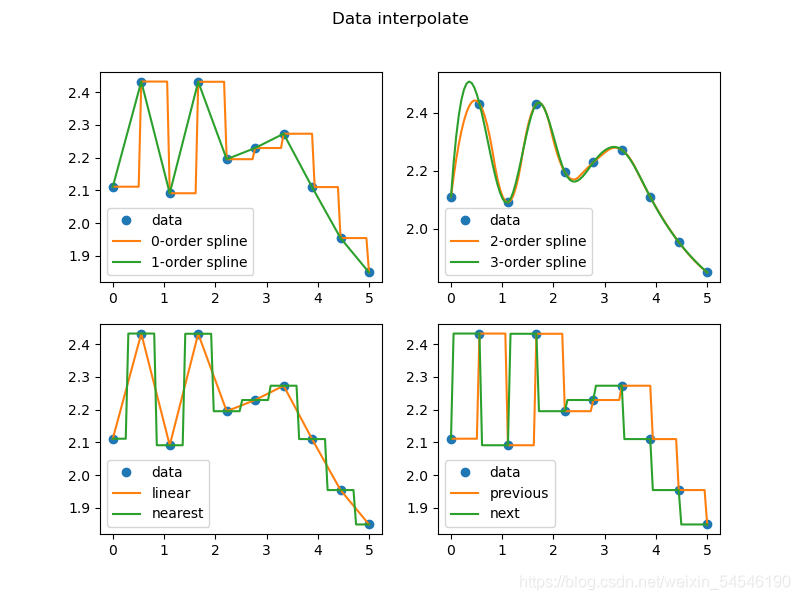
这里的‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’ 分别表示零次、一次、二次、三次样条插值;
3.1.2 一维插值方法的比较
此程序转载于youcans博主的博客:插值方法
# mathmodel24_v1.py
# Demo24 of mathematical modLSing algorithm
# Demo of interpolate with Scipy.interpolate
# Copyright 2021 YouCans, XUPT
# Crated:2021-08-01
#一维插值方法(内插)比较
import numpy as np
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
from scipy.interpolate import interp1d # 导入 scipy 中的一维插值工具 interp1d
# 生成已知数据点集 (x,y),需插值的数据点集 xnew
np.random.seed(5)
x = np.linspace(0, 5, 10) # 生成已知数据点集的 x
y = np.cos(x/10)*2 + 0.5*np.random.rand(10) # 生成已知数据点集的 y
xnew = np.linspace(0, 5, 100) # 指定需插值的数据点集 xnew
# 使用不同插值方法,由给定数据点集 (x,y) 求插值函数 fx
f1 = interp1d(x, y, kind="linear") # 线性插值
f2 = interp1d(x, y, kind="zero") # 零阶样条插值
f3 = interp1d(x, y, kind="slinear") # 一次样条插值
f4 = interp1d(x, y, kind="quadratic") # 二次样条插值
f5 = interp1d(x, y, kind="cubic") # 三次样条插值
f6 = interp1d(x, y, kind="nearest") # 临近点插值,向下舍入
# f7 = interp1d(x, y, kind="nearest-up") # 临近点插值,向上舍入
f8 = interp1d(x, y, kind="previous") # 前点插值
f9 = interp1d(x, y, kind="next") # 后点插值
# 绘图
plt.figure(figsize=(8,6))
plt.suptitle("Data interpolate") # 全局标题
plt.subplot(221)
plt.plot(x, y, "o", label="data") # 已知数据点
plt.plot(xnew, f2(xnew), label="0-order spline") # 零阶样条插值
plt.plot(xnew, f3(xnew), label="1-order spline") # 一阶样条插值
plt.legend(loc="lower left")
plt.subplot(222)
plt.plot(x, y, "o", label="data") # 已知数据点
plt.plot(xnew, f4(xnew), label="2-order spline") # 二阶样条插值
plt.plot(xnew, f5(xnew), label="3-order spline") # 三阶样条插值
plt.legend(loc="lower left")
plt.subplot(223)
plt.plot(x, y, "o", label="data") # 已知数据点
plt.plot(xnew, f1(xnew), label="linear") # 线性插值
plt.plot(xnew, f6(xnew), label="nearest") # 临近点插值,向下舍入
# plt.plot(xnew, f7(xnew), label="nearest-up") # 临近点插值,向上舍入
plt.legend(loc="lower left")
plt.subplot(224)
plt.plot(x, y, "o", label="data") # 已知数据点
plt.plot(xnew, f8(xnew), label="previous") # 前点插值
plt.plot(xnew, f9(xnew), label="next") # 后点插值
plt.legend(loc="lower left")
plt.show()
3.1.2 二维插值类 (interp2d)
interp2d(x,y,z,kind='linear', ...)
- x,y:已知的数据集的 x,y 值,都为一维数组。
- z:已知数据集的 z 值,可以为多维数组形式(注意:y 数组长度等于x,y 数组长度。)
- kind:字符串或整数,可选项,指定使用的样条曲线的种类或插值方法。 kind具体用法与一维插值函数(interp1d)没区别。
3.1.3 多维插值 (griddate)
Scipy.interpolate 模块中的griddata()函数具有强大的处理多维散列取样点进行插值运算的能力。如(二维散乱点插值)
griddata(points, values, xi, method='linear', fill_value=nan)
- points表示K维空间中的坐标,它可以是形状为(N,k)的数组,也可以是一个有k个数组的序列,N为数据的点数。
- values是points中每个点对应的值。xi是需要进行插值运算的坐标,其形状为(M,k),可通过numpy.meshgrid(,)构造网格节点获得。
- method参数有三个选项:‘nearest’、 ‘linear’、 ‘cubic’,分别对应0阶、1阶以及3阶插值。
3.2 numpy中多项式拟合函数(polyfit)
polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)
-
xarray_like:形状 (M,)
M 样本点的 x 坐标。(x[i], y[i]) -
yarray_like:形状(M)或(M,K)
样本点的 y 坐标。通过通过包含每个列包含一个数据集的 2D 阵列,可以同时安装几个共享相同 x 坐标的示例点数据集。 -
deg:拟合多面体的程度.deg = 2 :指拟合二次多项式。
详细信息请查看 polyfit官网
3.3 scipy.optimize模块中的函数curve_fit
The scipy.optimize module contains a least squares curve fit routine that requires as input a user-defined fitting function (in our case fitFunc ), the x-axis data (in our case, t) and the y-axis data (in our case, noisy). The curve_fit routine returns an array of fit parameters, and a matrix of covariance data (the square root of the diagonal values are the 1-sigma uncertainties on the fit parameters—provided you have a reasonable fit in the first place.):
fitParams, fitCovariances = curve_fit(fitFunc, t, noisy)
print fitParams
print fitCovariance
调用curve_fit()函数,核心步骤:
- 定义需要拟合的函数类型,如:
def func(x, a, b):
return 数据的拟合函数
# 如return c*y**2
-
调用
popt, pcov = curve_fit(func, x, y)函数进行拟合,并将拟合系数存储在popt中,a=popt[0]、b=popt[1]进行调用; -
调用
func(x, a, b)函数,其中x表示横轴表,a、b表示对应的参数。
3.4 一些小模块代码解释
3.4.1 numpy.linsapce()
numpy.linspace(start, stop, num=50)
start:返回样本数据开始点
stop:返回样本数据结束点
start和stop之间返回均匀间隔的数据
num:生成的样本数据量,默认为50
numpy.linsapce() 详细参考np.linspace用法介绍
3.4.2 pyplot.subplot()
plt.subplot(231) #把画布分成2*3的格子,把Y1放在第一格
plt。subplot(232)#把画布分成2*3的格子,把Y2放在第2格
plt.subplot(233)#把画布分成2*3的格子,把Y3放在第3格
例:在一行画两个图片
plt.subplot(121)
plt.subplot(122)
3.4.3 pyplot.contour()
contour()作用:绘制轮廓线,类于等高线 。
matplotlib.pyplot.contour([X, Y,] Z, [levels], ** kwargs)
- X,Y :值Z的坐标。
- X和Y必须都是2-D,且形状与Z相同,或者它们必须都是1-d,这样len(X)== M是Z中的列数,len(Y)== N是Z中的行数。
- Z : 绘制轮廓的高度值。
- levels: int或类数组,确定轮廓线/区域的数量和位置。
3.4.4 numpy.meshgrid(x, y)
作用:生成坐标矩阵
X,Y = numpy.meshgrid(x, y)
- 输入的x,y,就是网格点的横纵坐标列向量(非矩阵)
- 输出的X,Y,就是坐标矩阵。
3.4.5 np.linalg.norm()
作用:求相应的范数
x_norm=np.linalg.norm(x, ord=None)
# linalg=linear(线性)+algebra(代数),norm则表示范数。
- x: 表示矩阵(也可以是一维)
- ord:范数类型
详细可查看np.linalg.norm(求范数)
3.4.6 pyplot.clabel()
plt.cable(c,inline = True, fontsize = 10)
作用:定义等高线的标签。
- C:要标记的ContourSet(需要添加标签的线)。
- inline表示标签添加的位置:
- inline = True时,等高线在数字处会断开。
- inline = False时,等高线线会穿过数字。
- fontsize:以磅为单位的尺寸或相对尺寸,代表标签大小,例如‘smaller’,“ x-large”。
- colors:标签颜色:
- 如果为无,则每个标签的颜色与相应轮廓的颜色匹配。
- 如果使用一种字符串颜色(例如,颜色= ‘r’或颜色= ‘red’),则所有标签都将以此颜色绘制。
- 如果是matplotlib颜色args(字符串,float,rgb等)的元组,则将按照指定的顺序以不同的颜色绘制不同的标签。
(四)求解插值问题
4.1 一维插值
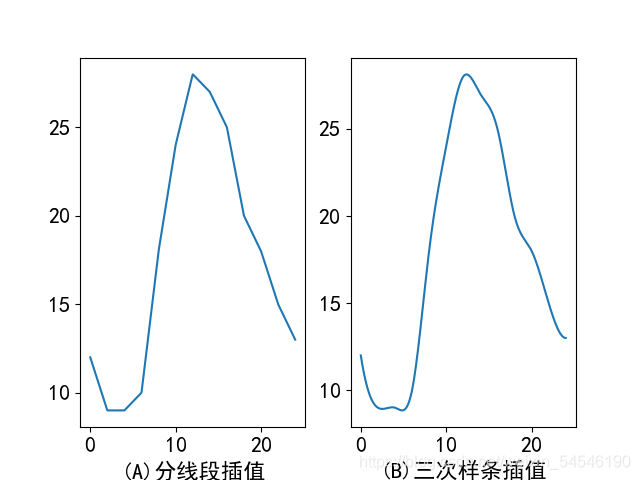
题目:在一天内,从0点开始每间隔 2h 测得环境温度如下表所示。分别进行分段线性插值和三次样条插值,并画出插值曲线。
| 时间 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 温度 | 12 | 9 | 9 | 10 | 18 | 24 | 28 | 27 | 25 | 20 | 18 | 15 | 13 |
# coding=utf-8
# 一维插值.py
# Copyright 2021 源仔
# Crated:2021-08-06
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
x = np.arange(0,25,2)
y = np.array([12,9,9,10,18,24,28,27,25,20,18,15,13])
xnew = np.linspace(0, 24, 500) # 生成0到25之间均匀间隔的500个插值点
f1 = interp1d(x,y); y1 = f1(xnew)
f2 = interp1d(x,y,'cubic') ; y2 = f2(xnew)
plt.rc('font',size=16); plt.rc('font',family='SimHei')
plt.subplot(121); plt.plot(xnew,y1) ; plt.xlabel("(A)分线段插值")
plt.subplot(122); plt.plot(xnew,y2) ; plt.xlabel("(B)三次样条插值")
plt.savefig("一维插值")
plt.show()
4.2 二维网格节点插值
已知ing面区域 0
≤
\le
≤ x
≤
\le
≤ 1400, 0
≤
\le
≤ y
≤
\le
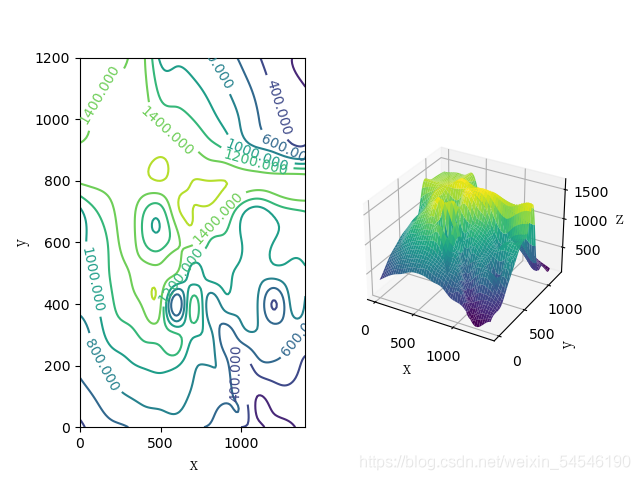
≤ 1200 的高程数据如下表所示(单位:m)。求该区域地表面积的近似值,并用插值数据画出该区域的登高线图和三位表面图。
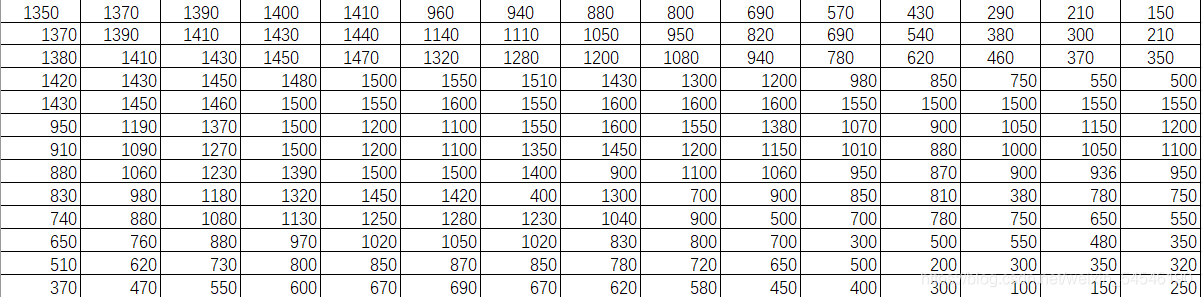
解: 原始数据给出 100
×
\times
× 100 网格节点的高程数据,为提高计算精度,利用双三次样条插值,得到给定区域 10
×
\times
× 10 网格节点上得搞成数据。
利用分点
x
i
x_i
xi?=10i (i=0,1,···,140)把 0
≤
\le
≤ x
≤
\le
≤ 1400 剖分成 140 个小区间,利用分点
y
i
y_i
yi? = 10j(j = 0,1,···,120)把 0
≤
\le
≤ y
≤
\le
≤ 1200 剖分成 120 个小区间,把平面区域 0
≤
\le
≤ x
≤
\le
≤ 1400,0
≤
\le
≤ y
≤
\le
≤ 1200 剖分成140
×
\times
× 120个小曲面进行计算,每个小区面的面积用对应的三位空间中 4 个点所构成的两个小三角形面积的和作为近似值。计算三角形面积时,使用海伦公式,即设
Δ
\Delta
ΔABC 的边长为 a,b,c,p = (a+b+c)/2,则
Δ
\Delta
ΔABC的面积 s =
p
(
p
?
a
)
(
p
?
b
)
(
p
?
c
)
\sqrt{p(p-a)(p-b)(p-c)}
p(p?a)(p?b)(p?c)?.
from matplotlib.font_manager import FontProperties
from scipy.interpolate import interp2d
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
import matplotlib.pyplot as pt
from numpy.linalg import norm
import pandas as pd
import numpy as np
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
z = pd.read_excel("数据表.xlsx",header=None)
x = np.arange(0,1500,100)
y = np.arange(1200,-100,-100)
f = interp2d(x,y,z,'cubic')
xn = np.linspace(0,1400,141)
yn = np.linspace(0,1200,121)
zn = f(xn,yn)
m = len(xn); n = len(yn); s = 0;
for i in np.arange(m-1):
for j in np.arange(n-1):
## p1,p2,p3,p4表示被解剖的小矩形的四个顶点
p1 = np.array([xn[i], yn[j], zn[j, i]])
p2 = np.array([xn[i+1], yn[j], zn[j, i+1]])
p3 = np.array([xn[i+1], yn[j+1], zn[j+1, i+1]])
p4 = np.array([xn[i], yn[j+1], zn[j+1, i]])
## norm表示范数,令 p1 = [2,3,4],p2 = [3,4,5],所以 p3 = p1-p2 = [1,1,1],则norm(p3)=1.73(根号3)
## 这里p12,p23,p13,p14,p34表示矩阵的边长和对角线长度
p12 = norm(p1-p2); p23 = norm(p3-p2); p13 = norm(p3-p1)
p14 = norm(p4-p1); p34 = norm(p4-p3)
## 这里用用的是 海伦公式 ,s1,s2表示小曲面矩形分成的两个小三角形面积
l1 = (p12+p23+p13)/2 ; s1 = np.sqrt(l1*(l1-p12)*(l1-p23)*(l1-p13))
l2 = (p13+p14+p34)/2 ; s2 = np.sqrt(l2*(l2-p13)*(l2-p14)*(l2-p34))
s = s + s1 + s2
print("区域面积为:",s)
# 图一
plt.subplot(121); contr = plt.contour(xn,yn,zn) ; plt.clabel(contr)
## plt.contour() 用于绘制等高线 ;plt.clabel(contr) :表示在等高线上显示高度
plt.xlabel('x', fontproperties=font) ;plt.ylabel("y", fontproperties=font,rotation=90)
# 图二
ax = plt.subplot(122,projection = '3d')
X,Y = np.meshgrid(xn,yn)
ax.plot_surface(X,Y,zn,cmap='viridis')
ax.set_xlabel('x', fontproperties=font); ax.set_ylabel('y', fontproperties=font,rotation=90); ax.set_zlabel('z', fontproperties=font)
plt.savefig('二维网格节点插值')
plt.show()
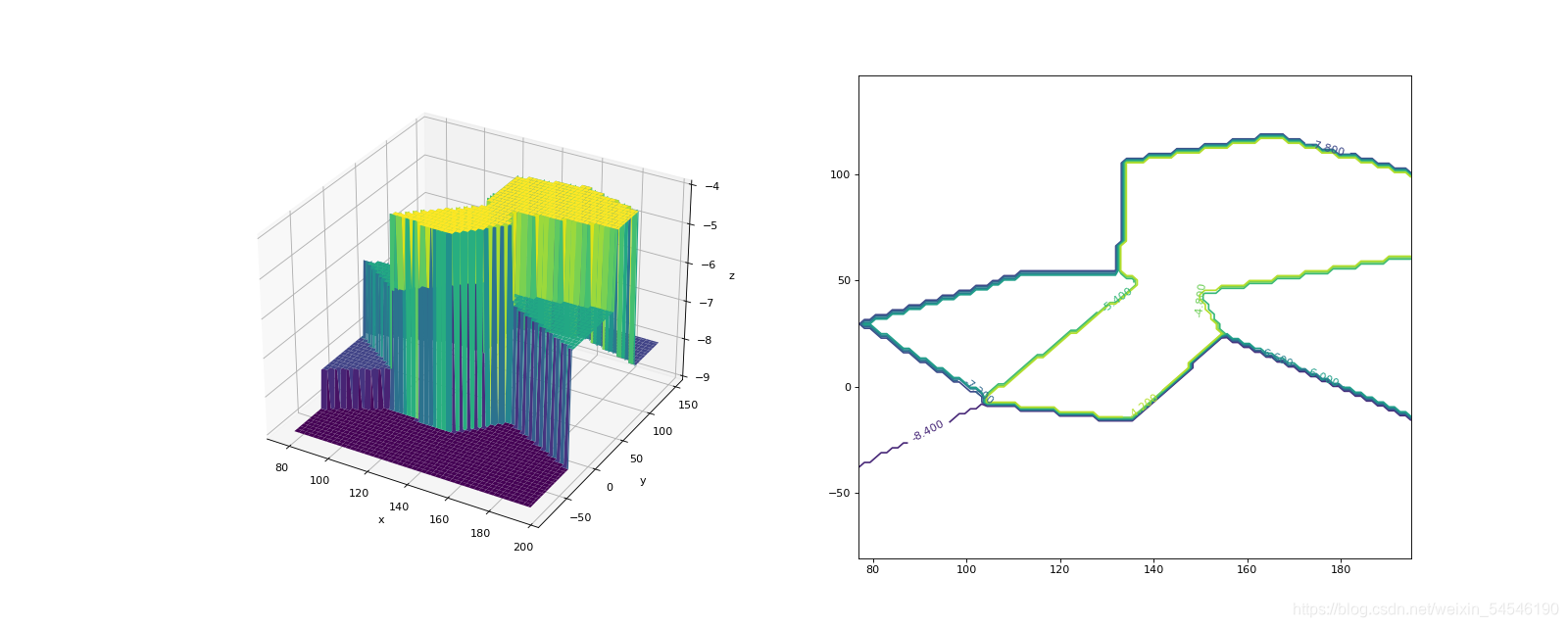
4.3 二维散乱点插值
问题 :在某海域测得一些点(x,y)处的水深 z 由下表给出,画出深海地区的地形和等高线。
| x | 129 | 140 | 103.5 | 88 | 185.5 | 195 | 105 | 157.5 | 107.5 | 77 | 81 | 162 | 162 | 117.5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 7.5 | 141.5 | 23 | 147 | 22.5 | 137.5 | 8525 | -6.5 | -81 | 3 | 56.5 | -66.5 | 84 | -33.5 |
| z | 4 | 8 | 6 | 8 | 6 | 8 | 8 | 9 | 9 | 8 | 8 | 9 | 4 | 9 |
from scipy.interpolate import griddata
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
import numpy as np
x = np.array([129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5])
y = np.array([7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5])
z = -np.array([4,8,6,8,6,8,8,9,9,8,8,9,4,9])
xy = np.vstack([x,y]).T
xn = np.linspace(x.min(),x.max(),100)
yn = np.linspace(y.min(),y.max(),100)
# 构造网格节点
xng,yng = np.meshgrid(xn,yn)
# 最近邻点插值
zn = griddata(xy,z,(xng,yng),method='nearest')
#设置图形的大小
plt.figure(figsize=(20,8),dpi=80)
ax = plt.subplot(121,projection='3d')
ax.plot_surface(xng,yng,zn,cmap='viridis')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
plt.subplot(122); c = plt.contour(xn,yn,zn,8); plt.clabel(c)
plt.savefig("二维散乱点插值.png")
plt.show()