[Python知识库]BinarySearch二分查找

前提元素要有序的情况下

def liner_search(li, val):
    for ind, v in enumerate(li):
        if v == val:
            return ind
    else:
        return None


def binary_search(li, val):
    left = 0
    right = len(li) - 1
    while left <= right:  # 候选区有值
        mid = (left + right) // 2  # 整除
        if li[mid] == val:
            return mid
        elif li[mid] > val:  # 说明查找值在左侧
            right = mid - 1
        else:  # 说明查找值在右侧时
            left = mid + 1
    return None


li2 = list(range(90000000))
print(binary_search(li2, 65000200))
print(liner_search(li2, 65000200))

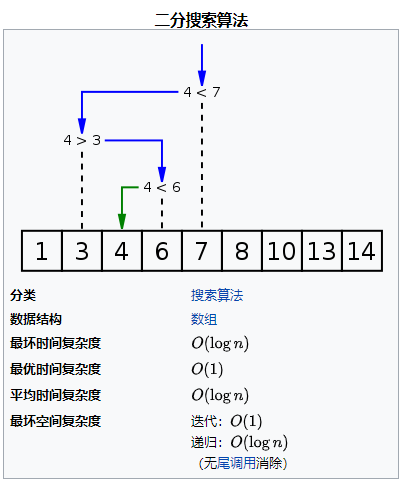
1. 二分搜索是什么？

二分搜索（英语：binary search），也叫折半搜索（英语：half-interval search），是一种在有序数组中查找特定元素的搜索算法。所以是用二分查找的前提是数组必须是有序的；时间复杂度，空间复杂度请参照下图；有的同学可能对时间复杂度和空间复杂的计算有点绕，我又在其他文章中介绍；

?

2. 下面通过代码讲解,注意了解下注释；

有关算法将基于python编写，如果你是javer，没有关系，你可以看的很轻松。

2.1 while循环方式

# python while循环版
def binary_search(list, item):
    low = 0
    hight = len(list) - 1
    while low <= hight:
        mid = (low + hight)//2  # 双斜线表示取整
        guess = list[mid]       # guess表示我们猜测mid位置即为我们要查找的元素
        if(guess == item):      # 如果我们猜中，返回下表
            return mid
        if(guess < item):       # 如果猜测的值比较小 那么我们从新的将区间定位的较大的区间
            low = mid + 1
        else:
            hight = mid - 1     # 如果猜测的时间比较大，我们把新的区间定位到较小的区间

    return None                 # 未能匹配到值

#test
my_list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
print(binary_search(my_list, 7))

2.2递归方式

# python 递归版
def binary_search2(low, hight, item, list):
    if(low > hight):
        return -1
    mid = low + (hight - low)//2 # 计算mid值，注意是 hight-low
    guess = list [mid]
    if(guess == item):
        return mid
    if(guess < item):
        return binary_search2(mid+1, hight, item, list) # 
    if(guess > item):
        return binary_search2(low, mid - 1, item, list)

#test
my_list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
print(binary_search2(0, len(my_list)-1, 7, my_list))