[Python知识库]Python数据可视化 | 1、数据可视化流程

1、数据准备

• 数据规模：数据分组、数据采样（处理大数据时候尤为需要）
• 数据类型：数值数据、分类数据（一定要对数据结构特别清楚：连续？离散？有序吗？）
• 数据规模：取值异常、数据缺失

数据分组 groupby

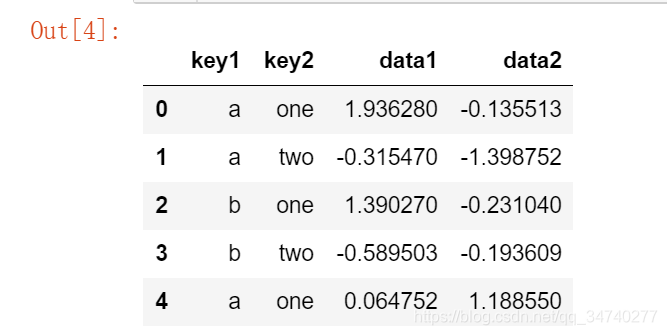
# DataFarme
df = pd.DataFrame({'key1':['a','a','b','b','a'],
                  'key2':['one','two','one','two','one'],
                  'data1':np.random.normal(size=5),
                  'data2':np.random.normal(size=5)})
df

df['data1'].groupby(df['key1']).mean()

数据采样 sample (处理大数据时尤为需要)

import random
x = np.arange(1,100)
y = random.sample(list(x),10)# 采样
y

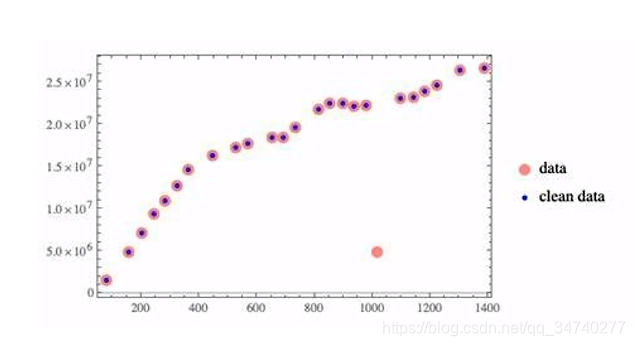
取值异常、数据缺失

1. 数据准备
2. 确定图表

NA处理 dropna fillna

# 去掉异常
x = np.arange(0,100)
y = x[(x>90)|(x<100)]
y

# 替换异常
y = x
for i in np.arange(0,100):
    if i >= 0 and i<=90:
        y[i] = 0
    else:
        y[i] = i
y

np.array([0 if i>= 10 and i <= 90 else i for i in range(0,100)])

# NA处理
from numpy import nan
data = pd.Series([1,nan,2,nan,3,nan])
data

data.dropna() # 删除空值

data.fillna(4) # 用4替换空值

2、确定图表

数据可视化里通常面临的三类问题：

• 关联分析：散点图，曲线图（scatter，plot）
• 分布分析：灰度图，密度图（hist，gaussian_kde，plot）
• 分类分析：柱状图，箱式图（bar，boxplot）

关联分析

from sklearn import datasets
import matplotlib.pyplot as plt
import seaborn as sns
bc = datasets.load_breast_cancer()
df = pd.DataFrame(bc.data,columns=bc.feature_names)
sns.lmplot('mean concavity','mean symmetry',df,
              height=5,aspect=1.5,fit_reg=True,order=4)

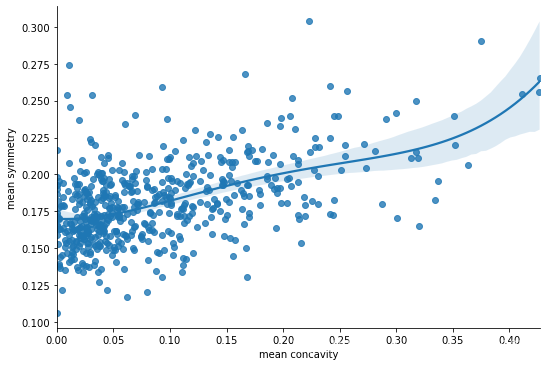
sns.lmplot('mean concavity','mean concave points',df,
              height=5,aspect=1.5,fit_reg=True,order=4)

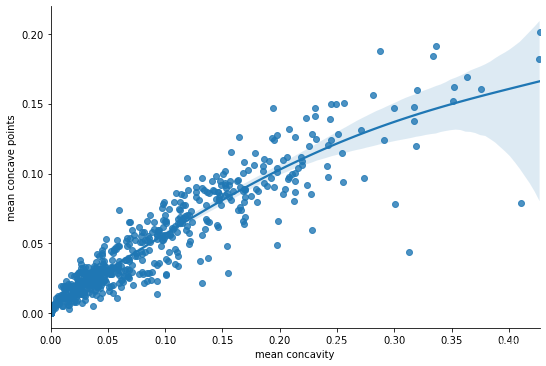
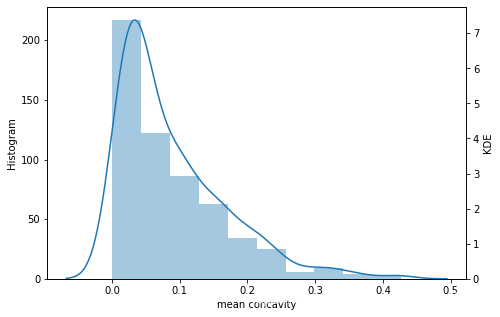
分布分析

plt.figure(figsize=(7.5,5))
sns.distplot(df['mean concavity'],bins=10,kde=False)
plt.ylabel('Histogram')
plt.twinx()
sns.kdeplot(df['mean concavity'],cumulative=False)
plt.ylabel('KDE')

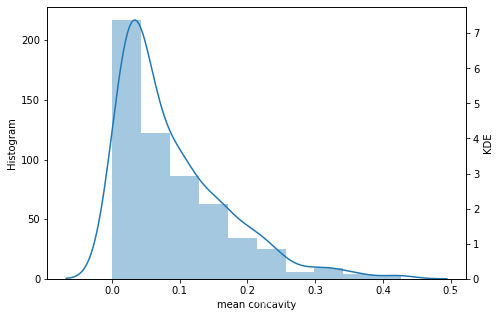
分类分析

plt.figure(figsize=(7.5,5))
sns.boxplot(x='mean concavity',data=df)

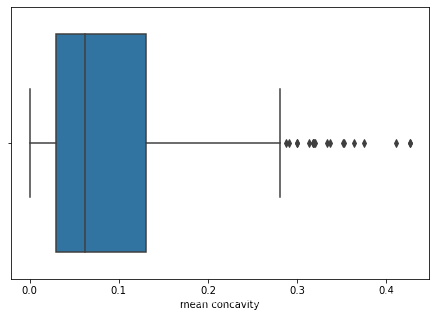
df['mean concavity'].describe()

3、分析迭代

• 确定拟合模型：OLS, fit OLS = 最小二乘；fit = 拟合
• 分析拟合性能：summary_table统计学汇总
• 确定数据分布：hist
• 确定重点区间：quartile 分布的上下四分位数，以及各分位数之间的区间

sns.lmplot('mean concavity','mean concave points',df,
              height=5,aspect=1.5,fit_reg=True,order=1)

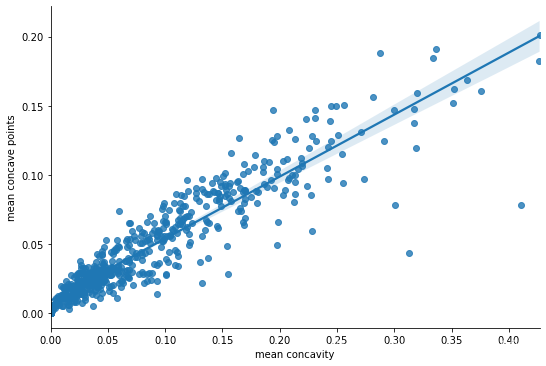
plt.figure(figsize=(7.5,5))
sns.distplot(df['mean concavity'],bins=10,kde=False)
plt.ylabel('Histogram')
plt.twinx()
sns.kdeplot(df['mean concavity'],kernel = 'gau',cumulative=False)
# sns.kdeplot(df['mean concavity'],kernel = 'gau',cumulative=False)
plt.ylabel('KDE')

plt.figure(figsize=(7.5,5))
sns.boxplot(x='mean concavity',data=df)

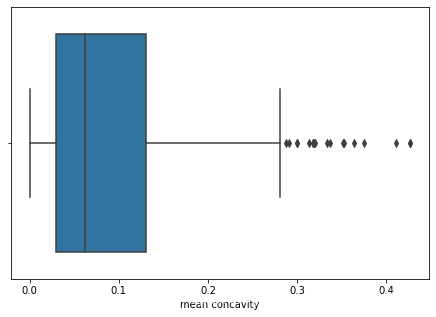
• 箱型图Boxplot
  观察分布的对称性和偏性
  
  
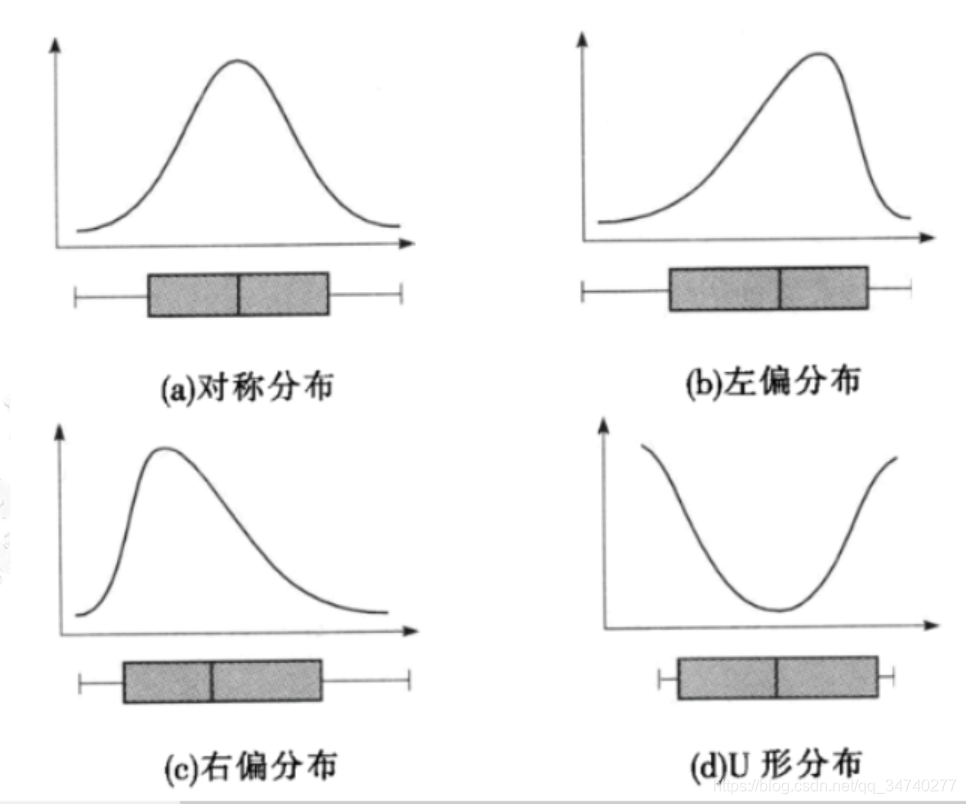
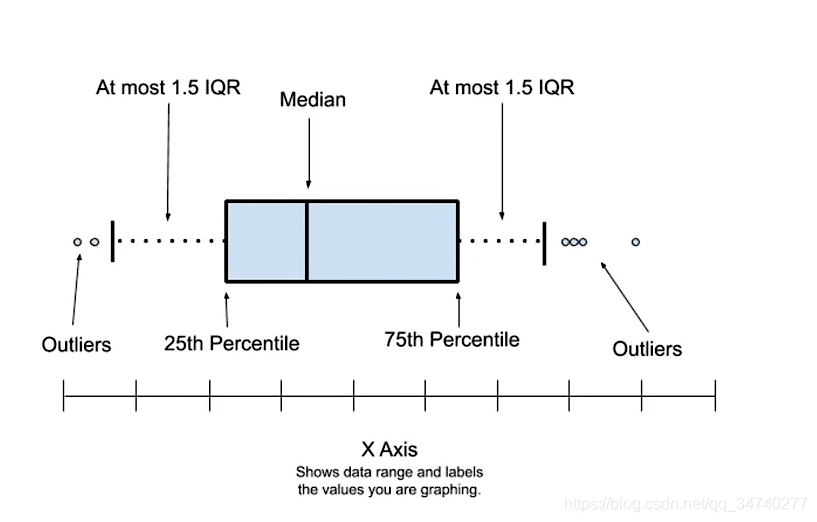
  箱型图的局限性
  
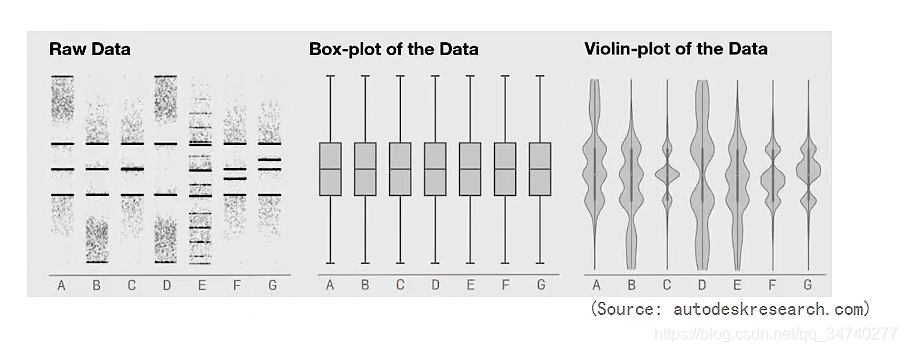
  对数据的本质理解会产生偏差，不同的数据集可能得到相同的箱型图。

"""
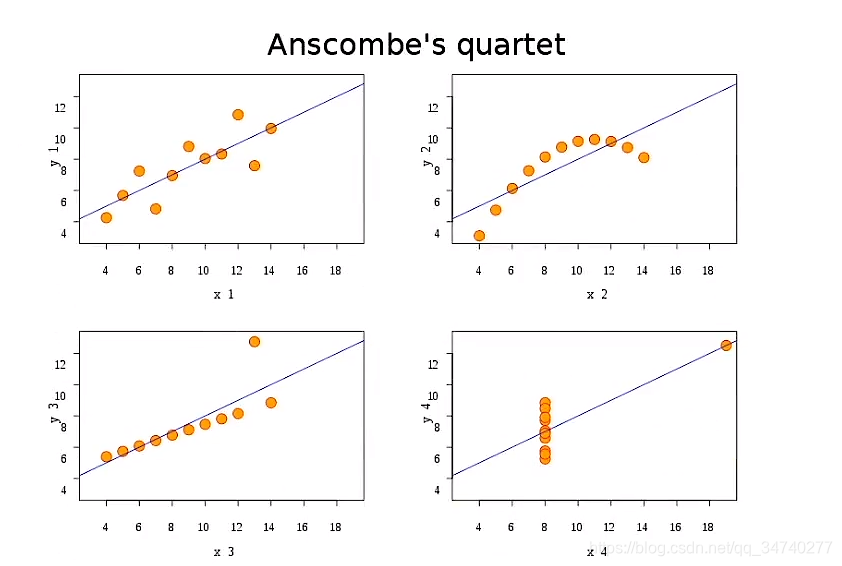
Edward Tufte uses this example from Anscombe to show 4 datasets of x
and y that have the same mean, standard deviation, and regression
line, but which are qualitatively different.
"""
x=[10,8,13,9,11,14,6,4,12,7,5] 
x4=[8,8,8,8,8,8,8,19,8,8,8]

y1=[8.04,6.95,7.58,8.81,8.33,9.96,7.24,4.26,10.84,4.82,5.68] 
y2=[9.14,8.14,8.74,8.77,9.26,8.10,6.13,3.10,9.13,7.26,4.74] 
y3=[7.46,6.77,12.74,7.11,7.81,8.84,6.08,5.39,8.15,6.42,5.73] 
y4=[6.58,5.76,7.71,8.84,8.47,7.04,5.25,12.50,5.56,7.91,6.89]
df=pd.DataFrame({'x':x,'y1':y1,'y2':y2,'y3':y3,'y4':y4,})
df[['y1','y2','y3','y4']].describe().loc['mean':'std']

分析迭代的要素，不仅依赖于数据本身，也依赖人的分析角度。

4、输出结论

• 养成看图说话的习惯
• 提出一个好问题，画出一个好图像，给出一个好结论
  
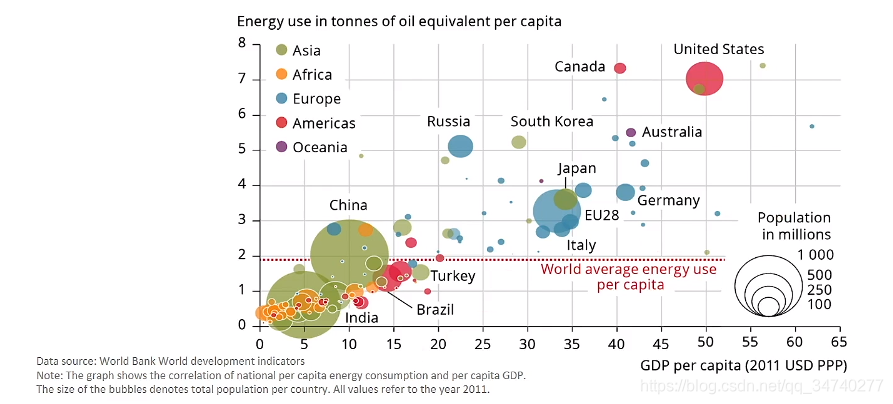
  结论：
  （1）人均GDP和石油消耗量成正比
  （2）人均GDP和石油消耗量与国家人口数量没有关系

5、小结

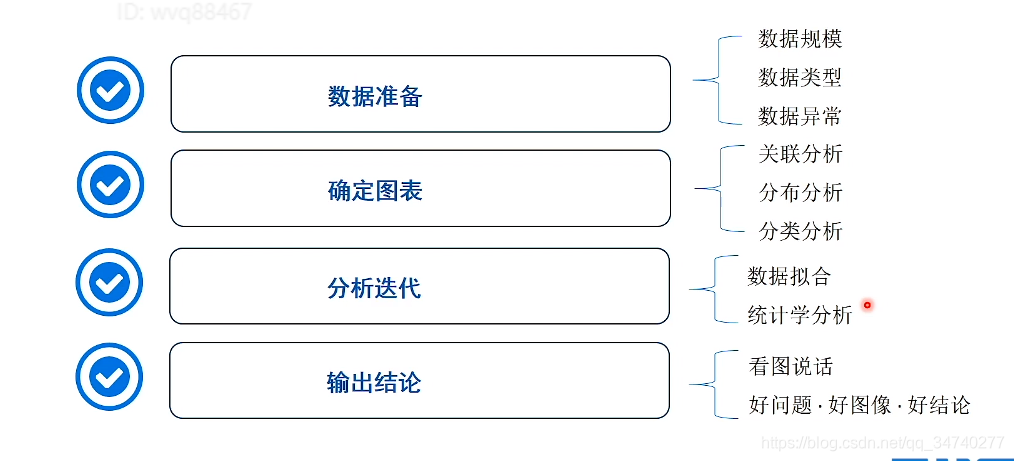
6、作业

绘制出Edward Tufte的散点图和一维拟合曲线，如下所示。（答案在下一篇文章公布）