关于均值
求解均值,例如有这么一组数据存放在Excel中,可能是所用的时间,可能是一些距离,可能是一些价格…等等
均值可能会受极端值的影响,所以比赛中常常去掉一个最高分去掉一个最低分,再求均值。
在含有极端值总体中,由于样本均值不具有耐抗性,往往难以代表"平均水平",
有时候也要考虑怎么处理这种极端情况,因为一两个偶然的结论数据就会导致一项研究的整个结论被改写。如何处理异常值是另外一件事情,且按下不表。

显然均值起源于统计学,统计学是数学的一个分支,它使我们能够有系统地分类、分析和解释数据。 统计经常用图形来表达。图形能够组织数据、表达数据之间的趋势和关系。
想象一下,如果每次需要切割一块木头时都需要重新制作锯,是不是太麻烦了。每次做锯,即使是完成同样的任务,也会出现许多人用不同的名称来命名这种工具。 为避免出现这种状况,我们给了这个工具一个名称,锯,每个人都可以引用它。
统计数据也是如此,我们拥有大家都熟悉的众所周知的工具,平均值mean就是这样一种工具,与此类似,还有众数mode、中位数median等。
- 均值(Mean) (1+2+3+3+5+7+7+8+9+10)/10 5.5 算术平均数。求和,除个数
- 中位数(Median) (5+7)/2 6 从小到大排序;选取中间的数求算术平均数
- 众数(Mode) 3,7 3,7 数据集中出现次数最多的数
python方法
读Excel数据
import xlrd
import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
from pandas import Series, DataFrame
data = xlrd.open_workbook('wjxData20210821.xls')
table = data.sheet_by_name('usedtime')
usedtime = table.col_values(3)[1:]
print(usedtime)
print(type(usedtime))
结果

统计变量说明
代码接上
df = pd.DataFrame(usedtime)
print(df.describe())

count:数量统计,此列共有多少有效值
mean:均值
std:标准差
min:最小值
25%:四分之一分位数
50%:二分之一分位数
75%:四分之三分位数
max:最大值
箱线图
代码接上
plt.grid(linestyle="--", alpha = 0.3)
df.boxplot()
plt.show()
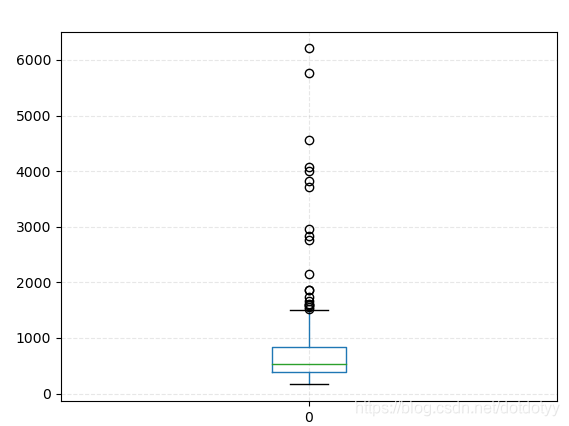
箱线图说明

求均值、众数等
代码接上
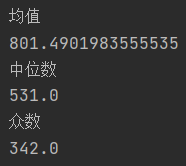
print("均值")
print(np.mean(usedtime)) #均值
print("中位数")
print(np.median(usedtime)) #中位数
print("众数")
print(stats.mode(usedtime)[0][0]) #众数