作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119854683
目录
前置参考:
[数值计算-10]:一元非线性函数求最小值 - 梯度下降法&Python法代码示例
https://blog.csdn.net/HiWangWenBing/article/details/119832688
第1章 多元非线性函数
1.1 什么是多元函数
设D为一个非空的n 元有序数组的集合, f为某一确定的对应规则。
若对于每一个有序数组?( x1,x2,…,xn)∈D,通过对应规则f,都有唯一确定的实数y与之对应,则称对应规则f为定义在D上的n元函数。
记为y=f(x1,x2,…,xn) 其中 ( x1,x2,…,xn)∈D。 变量x1,x2,…,xn称为自变量,y称为因变量。
当n=1时,为一元函数,记为y=f(x),x∈D,
当n=2时,为二元函数,记为z=f(x,y),(x,y)∈D。
二元及以上的函数统称为多元函数。
1.2 二元函数的几何图形
设D是二维空间R2的一个非空子集,称映射f:D→R为定义在D上的二元函数,通常记为
z=f(x,y),(x,y)∈D
其中点集D称为该函数的定义域,x、y称为自变量,z称为因变量.

如二元函数:z = f(x,y) =??x^2 + y^2 + 1
1.3. 函数的元与方程的元的区别
一元函数与二元方程:y= f(x)? => y - f(x) = 0
二元函数与三元方程:z= f(x,y)? => z?- f(x,y) = 0
第2章 向量vector
2.1 什么是向量
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。
与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
2.2?向量的维度
向量的投影轴的个数,就是向量的维度,如:?
(1)一维向量
A= [P1] = [Px] =【2】, 1维向量,投影值为2
(2)二维向量
A= [P1,P2] = [Px, Py] =【4,3】, 2维向量,在2个维度方向的投影值分别为4,3.

(3)三维向量
A= [P1,P2,P3] = [Px, Py, Pz] =【2,3,5】, 3维向量,在个3维度方向的投影值为2,3,5

2.3 向量的组成成分
就是向量在各个维度方向或数轴方向的投影,就是向量的成分,表示为:A= [P1,P2,P3, .....Pn]
2.4 向量的方向
箭头所指:代表向量的方向。
2.5 向量的大小
线段长度:代表向量的大小。

2.6 向量在此文中的作用
(1)描述多元函数在空间中任意点的坐标组成, 即不同维度方向上的数值。
(2)描述多元函数在空间中任意点的切线组成,即不同维度方向上切线/导数值。
- 切线向量最终的方向,就是梯度的方向。
- 切线向量在各个维度方向的分量,就是梯度在各个维度方向上的偏导数。
第3章 多元函数的偏导数/偏微分
3.1 一元函数的切线和导数

一元函数的切线和导数,有现成的公式求导数,如下图所示:

?那么,对于二元函数或多元函数,求导数,该如何计算呢?
这就需要用到偏导数的概念:通过临时固化其他维度分量的数值,用来求解多元函数在某个维度方向的导数或切线斜率。
然后,把所有维度方向的导数组成一个向量,就得到多元函数在空间中某一点处的导数或梯度P = {P1, P2, P3.....Pn}; 其中Pi是在i维度方向上的偏导数。
3.2 什么多元函数的偏导数/偏微分

其中:
x1, x2,....Xi......表示的是维度方向,而不是指在单个维度方向上的数值序列.?
{x1.0, x1.1, x1.2.....x1.n..}? 表示在x1的维度方向的序列
{x2.0, x2.1, x2.2.....x2.n..}? 表示在x2的维度方向的序列
{xi.0,? xi.1, xi.2? .....xi.n..}? 表示在x2的维度方向的序列
为了编码混淆,我们把不同的维度,使用不同的字母表示,并用二元函数为例:
z = f(x,y), 则在(xi,yi)处的偏导数为:

3.3 偏导数的计算方法
(1)导函数解析法
f'(x,y)|x 为f(x,y)在任意点(x,y)处相对于x的偏导函数 ,则在(xi,yi)处的对x的偏导数=?f'(xi,yi)|x
f'(x,y)|y?为f(x,y)在任意点(x,y)处相对于y的偏导函函,则在(xi,yi)处的对y的偏导数 =?f'(xi,yi)|y
(2)极限法
在(xi,yi)处对x求偏导:
?? ? ?
在(xi,yi)处对y求偏导:
? ? ? ?
(3)数值计算法(类似极限法)
详见:
[数值计算-9]:一元非线性函数求导数(数值微分)- 解析法与迭代法&Python法代码示例
https://blog.csdn.net/HiWangWenBing/article/details/119824982
第4章 梯度
4.1 什么梯度
在空间几何中,空间中的任意一点的梯度,就是一个向量,
4.2 梯度的标量表示法
?
4.3 梯度的向量表示法

4.4 梯度的复数表示

4.5 梯度的计算
梯度的计算就是偏导数的计算。
某个维度方向的梯度值 = 学习率 * 偏导数 * (-1)
第5章 梯度下降法求多元函数的极小值 - 原理
5.1 二元与一元函数梯度下降法的比较?
(1)一元函数的梯度下降法图示
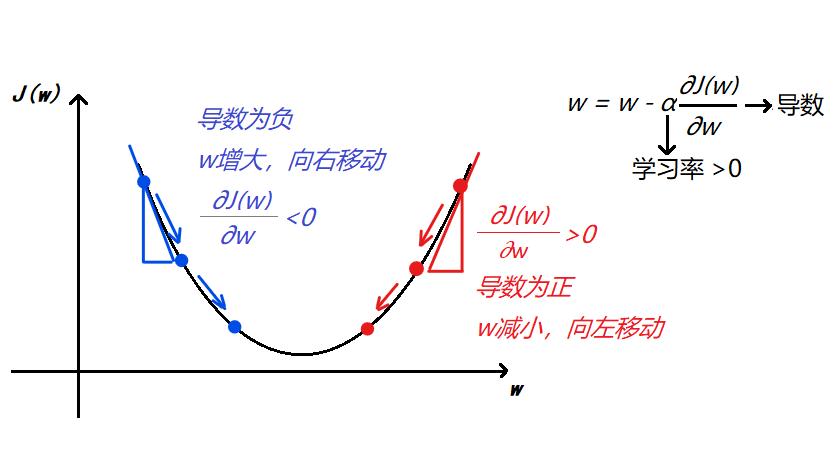
(2)二元函数的梯度下降法图示:
?
与一元函数的梯度下降法求极小值大体相同,主要区别在于:
- 由一元函数变成了多元函数
- 迭代的变量又一维变成了多维
- 每个维度方向由求导变成了求偏导
5.2 迭代算法
?
5.3?收敛条件
- 迭代次数
第6章 梯度下降法求多元函数的极小值 - 代码示例
6.1 前提条件
#导入库
from math import *
import time
import numpy as np
import matplotlib.pyplot as plt
6.2?二元函数图形
# 原函数:二元2次非线性函数
# y=f(x,y) = x^2 + y^2 + 1
def f(x,y):
return(1.0*x**2 + 1.0*y**2 + 1)
x = np.arange(-10, 10, 1)
y = np.arange(-10, 10, 1) #X,Y的范围
xd,yd = np.meshgrid(x,y) #空间的点序列转换成网格点
zd = f(xd,yd) #生成z轴的网格数据
figure = plt.figure()
ax1 = plt.axes(projection='3d') #创建三维坐标系
ax1.plot_surface(xd,yd,zd,rstride=1,cstride=1,cmap='rainbow')
#plt.show()#展示图片输出:

6.3?二元偏导函数图形
(1)对x的偏导函数
# 偏导函数:一阶对x的偏导函数
def fv1_x(x,y):
return(2*x) #导函数
# 函数图形: 对x的偏导函数
x = np.arange(-10, 10, 1)
y = np.arange(-10, 10, 1) #X,Y的范围
xd,yd = np.meshgrid(x,y) #空间的点序列转换成网格点
zd = fv1_x(xd,yd) #生成z轴的网格数据
figure = plt.figure()
ax1 = plt.axes(projection='3d') #创建三维坐标系
ax1.plot_surface(xd,yd,zd,rstride=1,cstride=1,cmap='rainbow')
#plt.show()#展示图片
输出:

(2)对y的偏导函数
# 偏导函数:一阶对y的导函数
def fv1_y(x,y):
return(2*y) #导函数
# 函数图形: 对y的偏导函数
x = np.arange(-10, 10, 1)
y = np.arange(-10, 10, 1) #X,Y的范围
xd,yd = np.meshgrid(x,y) #空间的点序列转换成网格点
zd = fv1_y(xd,yd) #生成z轴的网格数据
figure = plt.figure()
ax1 = plt.axes(projection='3d') #创建三维坐标系
ax1.plot_surface(xd,yd,zd,rstride=1,cstride=1,cmap='rainbow')
#plt.show()#展示图片
6.4?二元函数梯度下降法
(1)梯度下降法算法函数
# 梯度下降法求最小值的算法h(函数)
def fmin_gradient_descent(f, fv1_x, fv1_y, init_x0, init_y0, learning_rate, max_loop):
x_data = []
y_data = []
z_data = []
x_k = init_x0
x_k1 = init_x0
y_k = init_y0
y_k1 = init_y0
for k in range(max_loop):
#计算梯度
step_x = learning_rate * fv1_x(x_k, y_k)
step_y = learning_rate * fv1_y(x_k, y_k)
# 保存当前的迭代点
x_data.append(x_k1)
y_data.append(y_k1)
z_data.append(f(x_k1,y_k1))
x_k1 = x_k - step_x
y_k1 = y_k - step_y
# 为新一轮迭代做准备
x_k = x_k1
y_k = y_k1
z_k = f(x_k,y_k)
return ((x_k, y_k, z_k), (x_data, y_data, z_data))(2)梯度下降法运行:学习率=0.1
# 梯度下降法算法的使用
# 学习率=0.1,学习率较小,通过小步碎跑的方式逐步收敛域目标点。
result = fmin_gradient_descent(f,fv1_x, fv1_y, init_x0 = 10, init_y0 = 10, learning_rate = 0.1, max_loop =100)
print(result[0])
iter_x = result[1][0]
item_y = result[1][1]
item_z = result[1][2]
fig=plt.figure()
ax1 = plt.axes(projection='3d') #创建三维坐标系
ax1.scatter3D(iter_x,item_y,item_z, c='r', marker= '*')
(2.0370359763344878e-09, 2.0370359763344878e-09, 1.0)
Out[11]:
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x1dd0e292340>

(3)梯度下降法运行:学习率=0.5
# 梯度下降法算法的使用
# 学习率等于0.5时,为最佳迭代,无论Xk在哪里,都能够只需要一步迭代,就能够到目标点。
# 然后目标点的导数为0,后续的迭代步长为0,因为这里不可能是鞍点。
# 这就是导数(切线)的神奇之处,不同点,其导数不同值不同,不同点的迭代步长不同
# 但都能够保证,一次能够找到目标最小值点(后续的导数为0)
result = fmin_gradient_descent(f,fv1_x, fv1_y, init_x0 = 10, init_y0 = 10, learning_rate = 0.5, max_loop =100)
print(result[0])
iter_x = result[1][0]
item_y = result[1][1]
item_z = result[1][2]
fig=plt.figure()
ax1 = plt.axes(projection='3d') #创建三维坐标系
ax1.scatter3D(iter_x,item_y,item_z, c='r', marker= '*') (0.0, 0.0, 1.0)
Out[12]:
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x1dd0e2f3d60>

(4)梯度下降法运行:学习率=0.9
# 梯度下降法算法的使用
# 学习率=0.9,学习率较大,通过震荡的方式逐渐收敛到目标点。
result = fmin_gradient_descent(f,fv1_x, fv1_y, init_x0=10, init_y0=10, learning_rate = 0.9, max_loop =100)
print(result[0])
iter_x = result[1][0]
item_y = result[1][1]
item_z = result[1][2]
fig=plt.figure()
ax1 = plt.axes(projection='3d') #创建三维坐标系
ax1.scatter3D(iter_x,item_y,item_z, c='r', marker= '*') (2.0370359763344985e-09, 2.0370359763344985e-09, 1.0)
Out[15]:
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x1dd0e49f250>

作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119854683