Clark变换
作用
参考:
https://blog.csdn.net/chenjianbo88/article/details/53027298
https://zhuanlan.zhihu.com/p/147659820
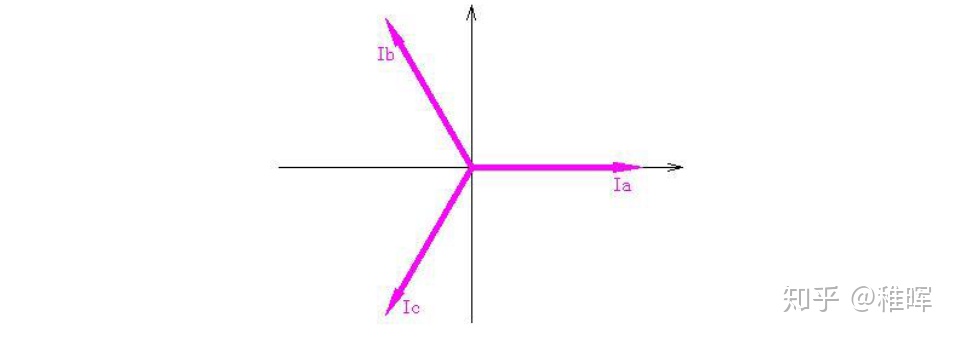
将 平面三相坐标系
I
a
I
b
I
c
I_aI_bI_c
Ia?Ib?Ic? 变换为 平面直角坐标系
I
α
I_\alpha
Iα?
I
β
I_\beta
Iβ?
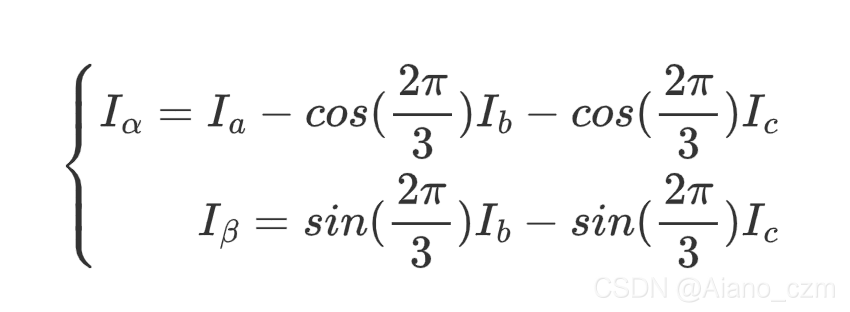
写成矩阵:
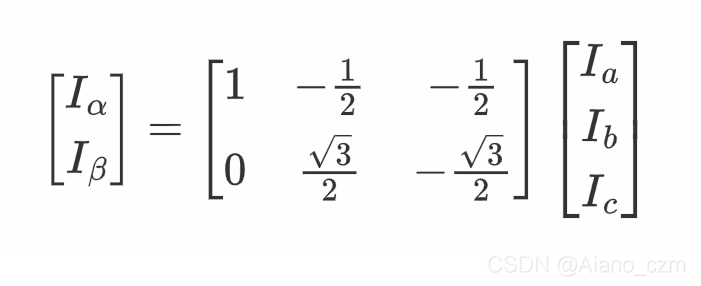
Python模拟
sin函数:https://blog.csdn.net/henni_719/article/details/77367294
正弦波信号:https://blog.csdn.net/weixin_39124421/article/details/103817951
np.linspace():https://blog.csdn.net/Asher117/article/details/87855493
import numpy as np
import matplotlib.pyplot as plt
def clark_transformation(input_matrix):
trans_arr = np.mat([[1, -1 / 2, -1 / 2], [0, np.sqrt(3) / 2, -np.sqrt(3) / 2]])
return trans_arr * input_matrix
def show_plot():
# init
plt.figure(figsize=(50,10))
# process
lin = np.linspace(0, 50, num=1000)
print(lin)
sin_wave1 = np.sin(lin)
phi = np.pi * 2 / 3
sin_wave2 = np.sin(lin - phi)
sin_wave3 = np.sin(lin - phi * 2)
# draw
plt.subplot(211)
plt.grid()
plt.title('Source')
plt.plot(lin, sin_wave1)
plt.plot(lin, sin_wave2)
plt.plot(lin, sin_wave3)
# clark transformation
trans_wave1 = np.empty(lin.shape)
trans_wave2 = np.empty(lin.shape)
for i in range(len(lin)):
input_array = np.mat([[sin_wave1[i]], [sin_wave2[i]], [sin_wave3[i]]])
output_array = clark_transformation(input_array)
trans_wave1[i] = output_array[0]
trans_wave2[i] = output_array[1]
# draw
plt.subplot(212)
plt.grid()
plt.title('Trans')
plt.plot(lin, trans_wave1)
plt.plot(lin, trans_wave2)
plt.show()
show_plot()
效果:
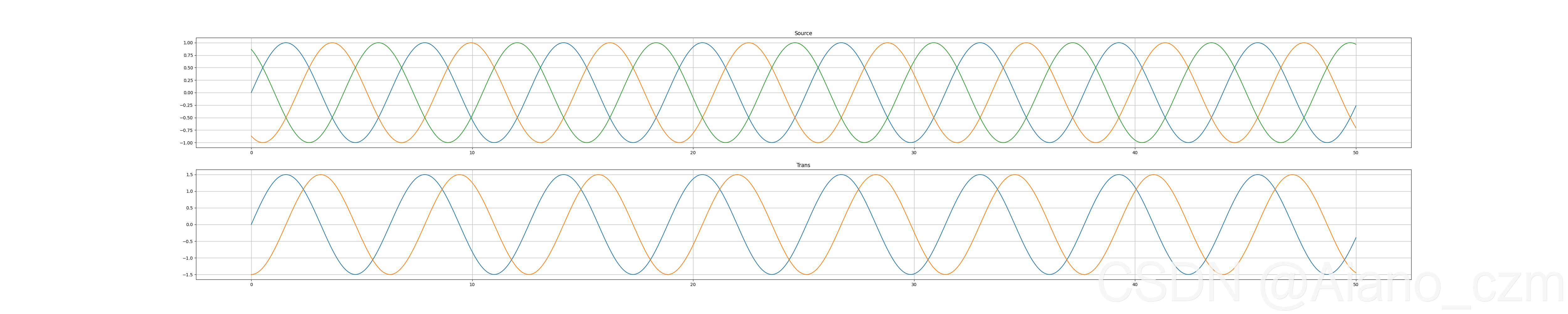
上图为相位相差 2 π 3 \frac{2\pi}{3} 32π?的三个正弦波
下图为经过Clark变换得到的两个正弦波
Park变换
作用
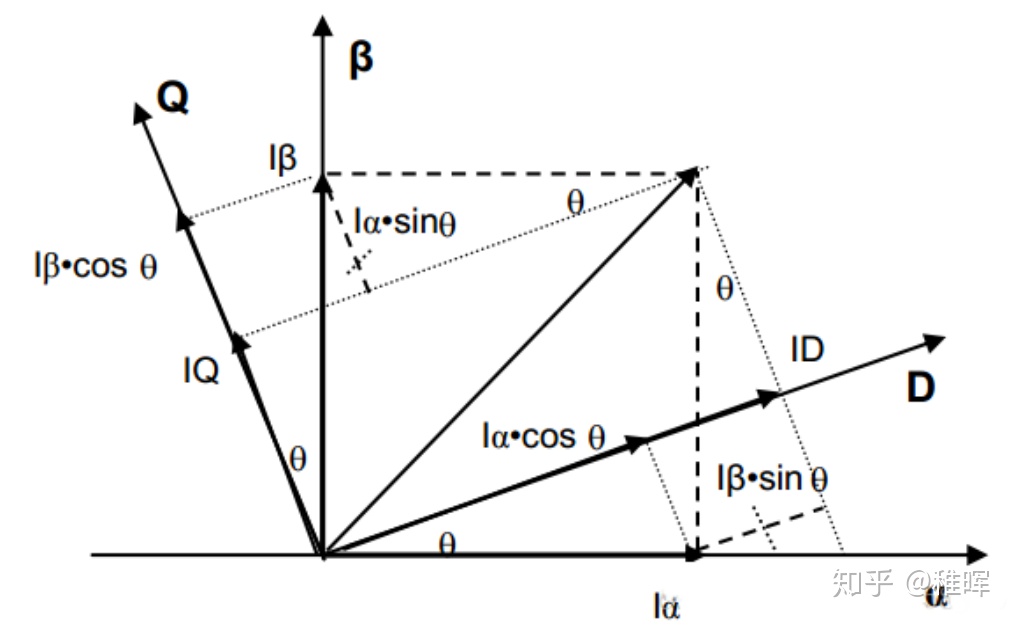
让新的坐标系跟着theta角旋转,使得投影到该坐标系上的值为定值,达到让非线性线性化的效果
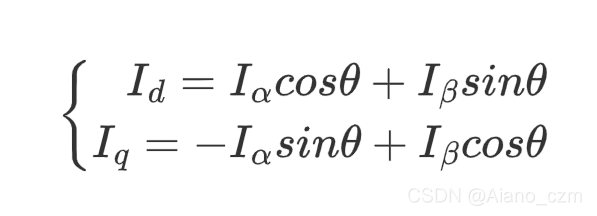
写成矩阵:(其实就是一个旋转矩阵)
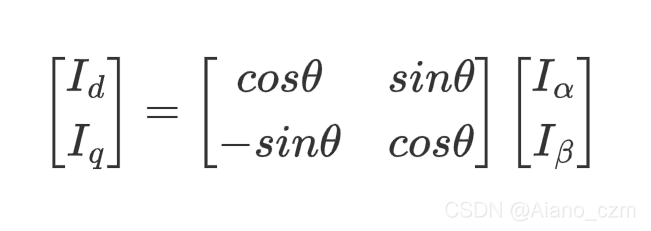
Python模拟
import numpy as np
import matplotlib.pyplot as plt
def clark_transformation(input_matrix):
trans_arr = np.mat([[1, -1 / 2, -1 / 2], [0, np.sqrt(3) / 2, -np.sqrt(3) / 2]])
return trans_arr * input_matrix
def park_transformation(input_matrix, theta):
trans_arr = np.mat([[np.cos(theta), np.sin(theta)], [-np.sin(theta), np.cos(theta)]])
return trans_arr * input_matrix
def show_plot():
# init
plt.figure(figsize=(20, 10))
# process
lin = np.linspace(0, 50, num=1000)
print(lin)
sin_wave1 = np.sin(lin)
phi = np.pi * 2 / 3
sin_wave2 = np.sin(lin - phi)
sin_wave3 = np.sin(lin - phi * 2)
# draw1
plt.subplot(311)
plt.grid()
plt.title('Source')
plt.plot(lin, sin_wave1)
plt.plot(lin, sin_wave2)
plt.plot(lin, sin_wave3)
# clark transformation
clark_trans_wave1 = np.empty(lin.shape)
clark_trans_wave2 = np.empty(lin.shape)
for i in range(len(lin)): # i means index, lin[i] means theta
input_array = np.mat([[sin_wave1[i]],
[sin_wave2[i]],
[sin_wave3[i]]])
output_array = clark_transformation(input_array)
clark_trans_wave1[i] = output_array[0]
clark_trans_wave2[i] = output_array[1]
# draw2
plt.subplot(312)
plt.grid()
plt.title('Clark')
plt.plot(lin, clark_trans_wave1)
plt.plot(lin, clark_trans_wave2)
# park transformation
park_trans_wave1 = np.empty(lin.shape)
park_trans_wave2 = np.empty(lin.shape)
for i in range(len(lin)): # i means index, lin[i] means theta
input_array = np.mat([[clark_trans_wave1[i]],
[clark_trans_wave2[i]]])
output_array = park_transformation(input_array, lin[i])
park_trans_wave1[i] = output_array[0]
park_trans_wave2[i] = output_array[1]
# draw3
plt.subplot(313)
plt.grid()
plt.title('Park')
plt.plot(lin, park_trans_wave1)
plt.plot(lin, park_trans_wave2)
# show plot
plt.show()
show_plot()
效果:
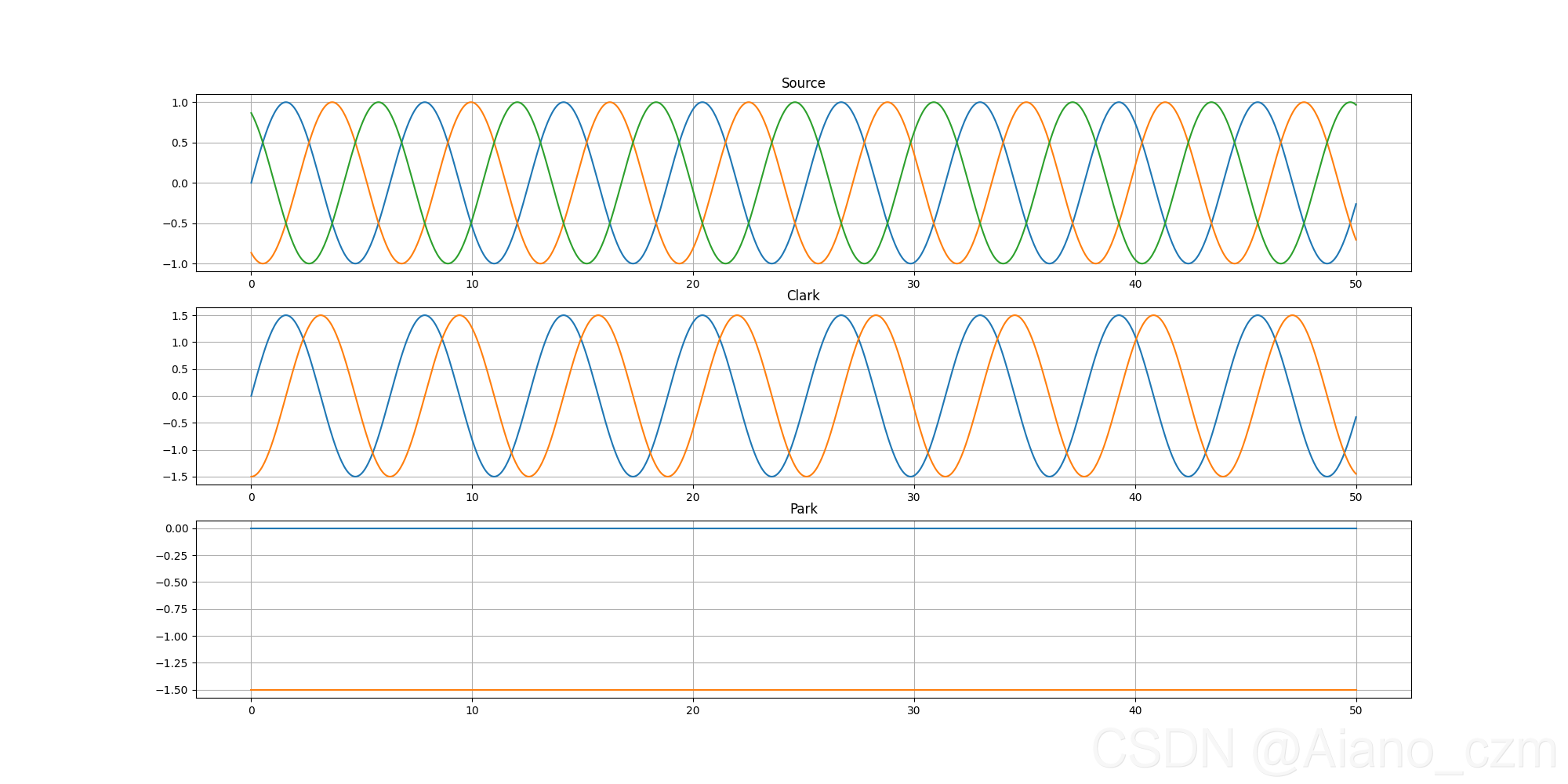
我是顺着Clark变换接着变换的,可以看出最终都是一条直线,是常量