学习复杂网络陷入误区,一直在思考度中心性是否需要加权?误认为中心性指标仅计算了度(无向网络中的度),没有考虑权重。结果忽略了中心性指标都是基于最短路径计算的(紧密中心性和中介中心性)。对此使用紧密中心性指标计算无权网络、加权网络、加权有向网络在数据基本一致的情况,该项指标是否有计算权重。
目录
一、无向无权网络
(一)数据
1.节点数据(节点数据没有变化)
(2)边数据(无权)(edge-11.txt)

(二)代码
import networkx as nx
import matplotlib.pyplot as plt
column1 = []
with open('node-9.txt','r') as f:
line = f.readline() # 读取一行
while line:
txt_data = eval(line) # 可将字符串变为元组
column1.append(txt_data) # 列表增加
line = f.readline() # 读取下一行
#print(column1)
edge = []
with open('edge-11.txt','r') as f:
line = f.readline() # 读取一行
while line:
txt_data = eval(line) # 可将字符串变为元组
edge.append(txt_data) # 列表增加
line = f.readline() # 读取下一行
#print(edge)
G = nx.Graph()
G.add_nodes_from(column1)
G.add_edges_from(edge)
nx.draw_networkx(G,pos=nx.shell_layout(G),node_size=20,node_shape='o',width=1,style='solid',font_size=8)
plt.show()
#计算紧密中心度(无权重无向)
print("无权重无向Closeness centrality")
c = nx.closeness_centrality(G)
for v in G.nodes():
print(v, c[v])
结果
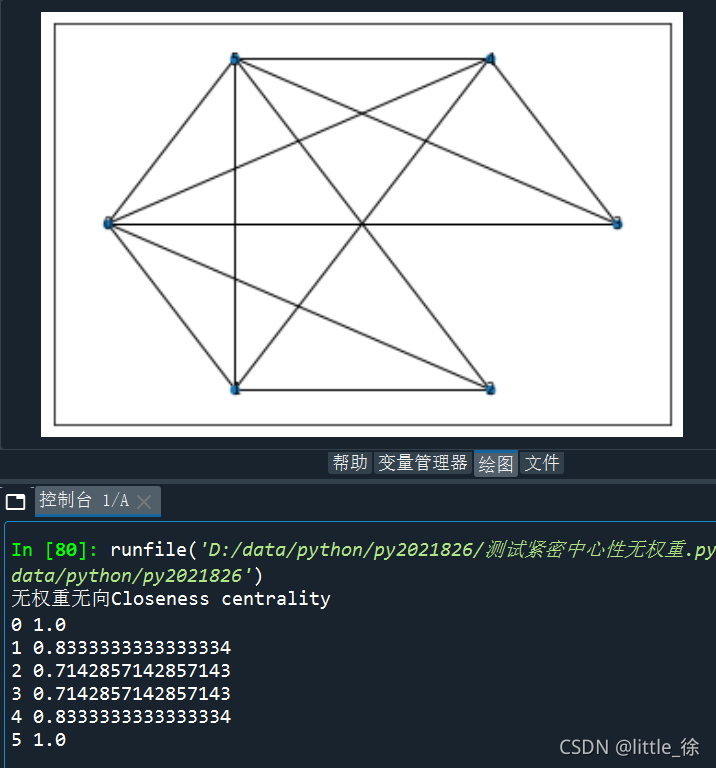
二、无向加权网络
(一)数据
1.节点数据(节点数据没有变化)
(2)边数据(加权)(edge-10.txt)
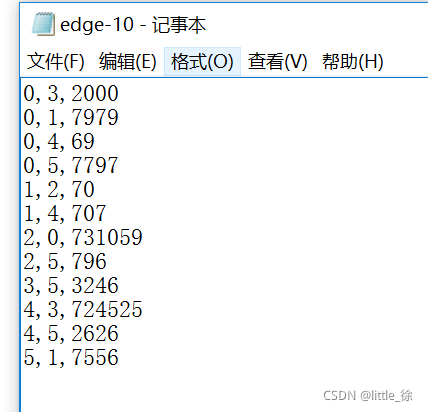
(二)代码
import networkx as nx
import matplotlib.pyplot as plt
column1 = []
with open('node-9.txt','r') as f:
line = f.readline() # 读取一行
while line:
txt_data = eval(line) # 可将字符串变为元组
column1.append(txt_data) # 列表增加
line = f.readline() # 读取下一行
#print(column1)
edge = []
with open('edge-10.txt','r') as f:
line = f.readline() # 读取一行
while line:
txt_data = eval(line) # 可将字符串变为元组
edge.append(txt_data) # 列表增加
line = f.readline() # 读取下一行
#print(edge)
G = nx.Graph()
G.add_nodes_from(column1)
G.add_weighted_edges_from(edge)
nx.draw_networkx(G,pos=nx.shell_layout(G),node_size=20,node_shape='o',width=1,style='solid',font_size=8)
plt.show()
####------紧密中心性-------#########
#计算紧密中心度(有权重无向)
print("无向加权Closeness centrality")
c = nx.closeness_centrality(G)
for v in G.nodes():
print(v, c[v])
结果
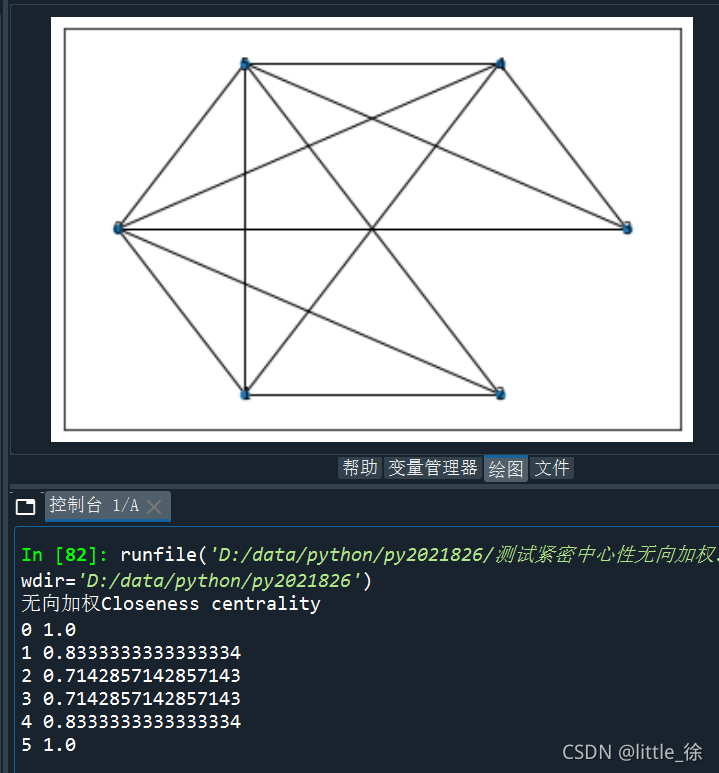
三、加权有向网络(变化权重)
(一)数据
1.节点数据(节点数据没有变化)
(2)边数据(加权)

(二)代码
import networkx as nx
import matplotlib.pyplot as plt
column1 = []
with open('node-9.txt','r') as f:
line = f.readline() # 读取一行
while line:
txt_data = eval(line) # 可将字符串变为元组
column1.append(txt_data) # 列表增加
line = f.readline() # 读取下一行
#print(column1)
edge = []
with open('edge-10.txt','r') as f:
line = f.readline() # 读取一行
while line:
txt_data = eval(line) # 可将字符串变为元组
edge.append(txt_data) # 列表增加
line = f.readline() # 读取下一行
#print(edge)
G = nx.DiGraph()
G.add_nodes_from(column1)
G.add_weighted_edges_from(edge)
nx.draw_networkx(G,pos=nx.shell_layout(G),node_size=20,node_shape='o',width=1,style='solid',font_size=8)
plt.show()
####------紧密中心性-------#########
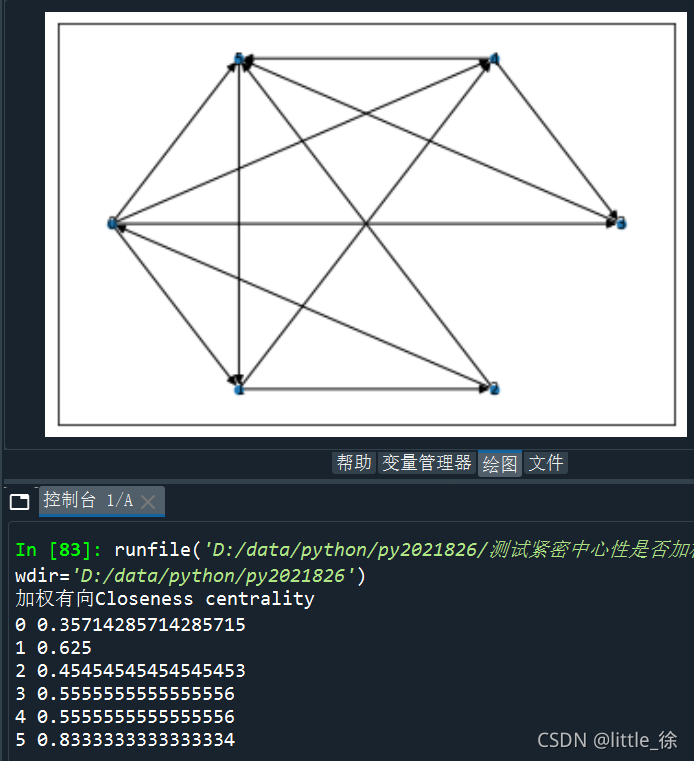
#计算紧密中心度(加权有向)
print("加权有向Closeness centrality")
c = nx.closeness_centrality(G)
for v in G.nodes():
print(v, c[v])
结果
四、加权为1有向网络
(一)数据
1.节点数据(节点数据没有变化)
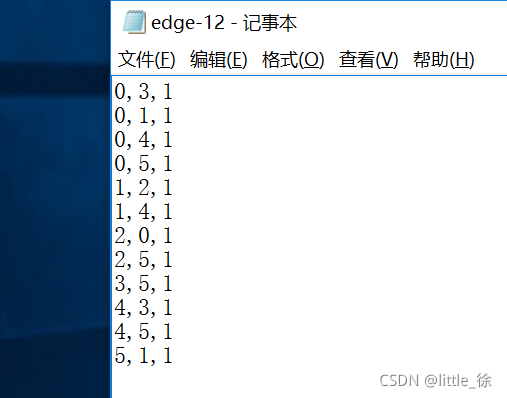
(2)边数据(加权为1)(edge-12.txt)
(二)代码
import networkx as nx
import matplotlib.pyplot as plt
column1 = []
with open('node-9.txt','r') as f:
line = f.readline() # 读取一行
while line:
txt_data = eval(line) # 可将字符串变为元组
column1.append(txt_data) # 列表增加
line = f.readline() # 读取下一行
#print(column1)
edge = []
with open('edge-12.txt','r') as f:
line = f.readline() # 读取一行
while line:
txt_data = eval(line) # 可将字符串变为元组
edge.append(txt_data) # 列表增加
line = f.readline() # 读取下一行
#print(edge)
G = nx.DiGraph()
G.add_nodes_from(column1)
G.add_weighted_edges_from(edge)
nx.draw_networkx(G,pos=nx.shell_layout(G),node_size=20,node_shape='o',width=1,style='solid',font_size=8)
plt.show()
####------紧密中心性-------#########
#计算紧密中心度(加权有向)
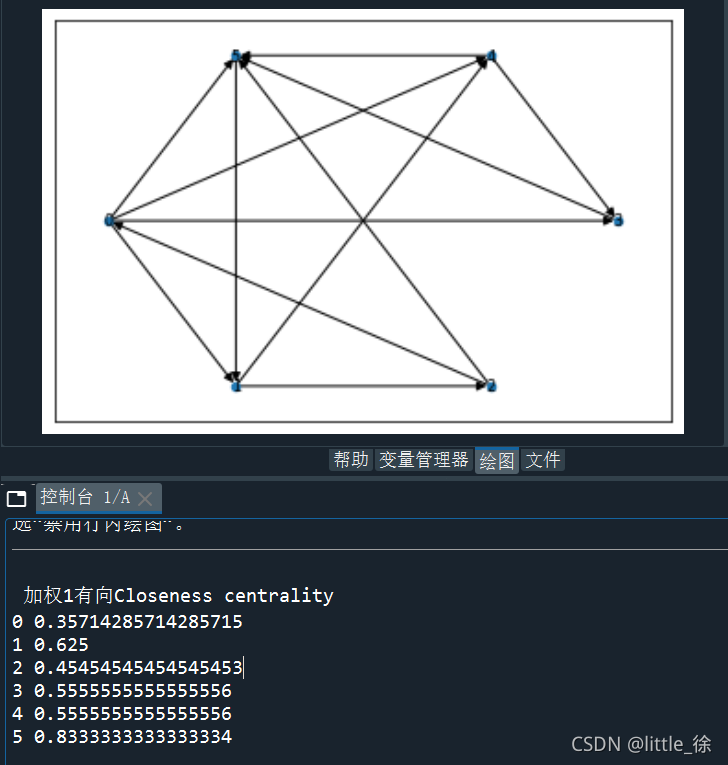
print("加权1有向Closeness centrality")
c = nx.closeness_centrality(G)
for v in G.nodes():
print(v, c[v])
结果
五、结果
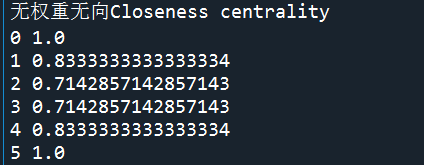
无向无权结果:
无向加权结果:
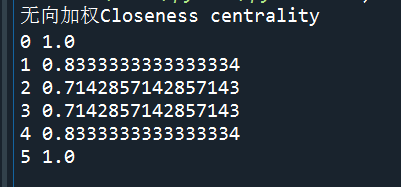
加权(带权重)有向结果:
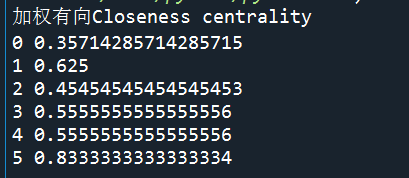
加权(加权为1)有向结果:
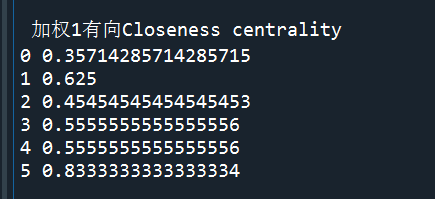
对比结果可以发现,紧密中心性在无向网络和有向网络中计算结果是不一致的,但是无向无权和无向加权网络中的紧密中心性结果一致,有向加权为1和有向加权(随机权重)网络中的紧密中心性结果一致,因此可以得出结论:无向和有向网络紧密中心性计算结果不一致;但是有向网络中,权重并没有影响紧密中心性,紧密中心性closeness_centrality中使用的Dijkstra算法并没有使用边的权重。对此,就要思考,Dijkstra算法可以添加属性权重,closeness_centrality在“拿来用”的时候,是怎么把这个属性显示出来?
对此可以观察下紧密中心性的计算原理:
亲近中心性的计算步骤:
1.使用Dijkstra算法计算每对节点间的最短路径,并将这些距离存储在一张表中。
2.对每个节点:a. 计算所有其他节点的平均距离 b.除以最大距离 c.亲近性=1/平均距离
其结果是一个介于0到1的数值:值越高意味着亲近中心性更大(平均距离越低)。(更常见的是将该分数归一化,使该得分代表最短路径的平均长度,而不是它们的总和。这种调整允许比较不同大小图节点的紧密性中心性。)
归一化后的紧密中心性公式如下:

在这个公式中
- u是一个节点。
- n是图中的节点数。
- d(u,v)是另一个节点V和U之间的最短路径距离。(Dijkstra算法)
再来看下Networkx官方给出的函数:

(closeness distance 函数计算有 向图的传入距离。要使用向外距离。)
发现这个函数可以添加参数:

因此可以猜想,这个是否就是继承Dijkstra算法添加权重的参数呢?接下来使用权重为1和权重随机的有向网络对比验证一下。
六、正确添加权重
c = nx.closeness_centrality(G,distance='weight')
下面的区别是边的数据不一样
1.加权(随机)有向网络
边数据:edge-10.txt
print("加权有向Closeness centrality")
c = nx.closeness_centrality(G,distance='weight')
for v in G.nodes():
print(v, c[v])
结果1:
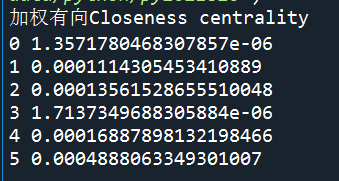
2.加权为1有向网络
边数据:edge-12.txt
#计算紧密中心度(加权为1有向)
print("加权1有向Closeness centrality")
c = nx.closeness_centrality(G,distance='weight')
for v in G.nodes():
print(v, c[v])
结果2:
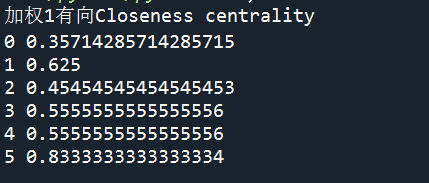
结果不一致,而且结果2和未加distance='weight’的加权(带权重)有向结果、加权(加权为1)有向结果一致(详看第五章 五、结果),说明在未写distance参数时,distance默认为1,nx.closeness_centrality(G,distance=1)。
通过网络查询,ucinet计算紧密中心性是可以选择是否加权,说明其实这个软件基本满足我们的需求。由于一开始就是学习gephi,而且可视化较好,就不再学习ucinet去验证了。会使用的小伙伴可以拿这个数据去验证下。
(写于2021.8.26;2021.8.27修改,增加第六章。)