1. 题目
你在一个城市里,城市由 n 个路口组成,路口编号为 0 到 n - 1 ,某些路口之间有 双向 道路。
输入保证你可以从任意路口出发到达其他任意路口,且任意两个路口之间最多有一条路。
给你一个整数 n 和二维整数数组 roads ,其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。
你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。
请返回花费 最少时间 到达目的地的 路径数目 。
由于答案可能很大,将结果对 10^9 + 7 取余 后返回。
示例 1:
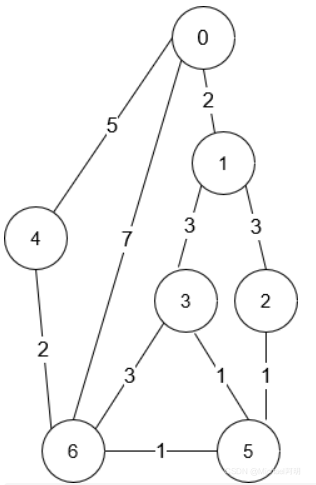
输入:n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],
[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
输出:4
解释:从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为:
- 0 ? 6
- 0 ? 4 ? 6
- 0 ? 1 ? 2 ? 5 ? 6
- 0 ? 1 ? 3 ? 5 ? 6
示例 2:
输入:n = 2, roads = [[1,0,10]]
输出:1
解释:只有一条从路口 0 到路口 1 的路,花费 10 分钟。
提示:
1 <= n <= 200
n - 1 <= roads.length <= n * (n - 1) / 2
roads[i].length == 3
0 <= ui, vi <= n - 1
1 <= timei <= 10^9
ui != vi
任意两个路口之间至多有一条路。
从任意路口出发,你能够到达其他任意路口。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-ways-to-arrive-at-destination
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
2. 解题
- 迪杰斯特拉 最短路径,优先队列
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
from queue import PriorityQueue
q = PriorityQueue()
g = [[] for _ in range(n)]
for r in roads:
g[r[0]].append((r[1], r[2]))
g[r[1]].append((r[0], r[2]))
time_roadnums = [[int(1e15), 0] for _ in range(n)]
# 存储 【最短时间,方案数】
time_roadnums[0][0] = 0
time_roadnums[0][1] = 1
q.put([0, 0]) # [时间,id] 第一个参数小的优先
while not q.empty():
t, id = q.get()
for it in g[id]:
nid, times = it
if time_roadnums[nid][0] > t+times: # 更短时间
time_roadnums[nid][0] = t+times
time_roadnums[nid][1] = time_roadnums[id][1] # 方案数清空,换成当前的
q.put([t+times, nid])
elif time_roadnums[nid][0] == t+times: # 相同时间
time_roadnums[nid][1] += time_roadnums[id][1] # 方案数累加
return time_roadnums[n-1][1]%int(1e9+7)
80 ms 20.9 MB Python3
顺便问一句,Python 优先队列 怎么改 优先级为 大的优先?请大家赐教
我的CSDN博客地址 https://michael.blog.csdn.net/
长按或扫码关注我的公众号(Michael阿明),一起加油、一起学习进步!
