开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> Python知识库 -> python数学建模（四）微分方程模型 -> 正文阅读

[Python知识库]python数学建模（四）微分方程模型

（源）本编博客源代码下载

python建模会持续更新，用途是只作为个人笔记。我博客中的所有资料都可通过我提供的链接永久获取，希望大家一起相互促进，相互努力。

本文所有代码、资料获取链接：
求解微分方程代码
提取码：z4i6
–来自百度网盘超级会员V2的分享

（一）用python求解微分方程

1.1 求微分方程（方程组）的符号解

Sympy 库提供了 dsolve 函数求微分方程的符号解。在声明时可以使用Function 函数将符号变量声明为函数类型。如下：

y = Function('y')
或
y = symbols(‘y’, cls=Function)

例一：求微分方程的通解
（1）齐次方程： $\frac{\partial^2 y}{\partial x^2}-5\frac{\partial y}{\partial x}+6y =0;$
（2）非齐次方程： $\frac{\partial^2 y}{\partial x^2}-5\frac{\partial y}{\partial x}+6y = xe^{2x}.$

# coding=utf-8
# 求微分方程（方程组）的符号解 例一
# Copyright  源仔
# Crated：2021-08-25

from sympy import *

x = symbols('x'); y = symbols('y',cls=Function)
eq1 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)
eq2 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)-x*exp(2*x)
print("齐次方程的解为：",dsolve(eq1,y(x)))
print("非齐次方程的解为：",dsolve(eq2,y(x)))

OUT:
	齐次方程的解为： Eq(y(x), (C1 + C2*exp(x))*exp(2*x))
	非齐次方程的解为： Eq(y(x), (C1 + C2*exp(x) - x**2/2 - x)*exp(2*x))

例二：
（1）初值问题： $\frac{\partial^2 y}{\partial x^2}-5\frac{\partial y}{\partial x}+6y =0，y(0)=1,\frac{\partial y}{\partial x} |_ {x=0}=0;$
（2）初值问题： $\frac{\partial^2 y}{\partial x^2}-5\frac{\partial y}{\partial x}+6y = xe^{2x}，y(0)=1,y(2)=0$

# coding=utf-8
# 求微分方程（方程组）的符号解 例二
# Copyright  源仔
# Crated：2021-08-25

from sympy import *

x = symbols('x'); y = symbols('y',cls=Function)
eq1 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)
eq2 = diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)-x*exp(2*x)
print("初值问题的解为：{}".format(dsolve(eq1,y(x),ics={y(0):1,diff(y(x),x).subs(x,0):0})))
y2 = dsolve(eq2,y(x),ics={y(0):1,y(2):0})
print("边值问题的解为：{}".format(y2))

 O U T:
	初值问题的解为：Eq(y(x), (3 - 2*exp(x))*exp(2*x))
	边值问题的解为：Eq(y(x), (-x**2/2 - x + 3*exp(x)/(-1 + exp(2)) + (-4 + exp(2))/(-1 + exp(2)))*exp(2*x))

例三：求下述微分方程的解：
$\begin{cases} \frac{\partial^2 y}{\partial x^2}+2\frac{\partial y}{\partial x}+2y =sinx,&\\ y(0) = 0, \frac{\partial y}{\partial x}|_{x=0}=1. \end{cases}$

# coding=utf-8
# 求微分方程（方程组）的符号解：例三
# Copyright  源仔
# Crated：2021-08-25

# 引入符号变量 x
from sympy.abc import x
from sympy import Function, diff, dsolve, sin

y = Function('y')
eq = diff(y(x),x,2)+2*diff(y(x),x)+2*y(x)-sin(x)  # 定义方程
con = {y(0): 0,diff(y(x), x).subs(x,0): 1}        # 定义初值条件
y = dsolve(eq, ics=con)
print("# Copyright  源仔")
print(y)

OUT:

	# Copyright  源仔
	Eq(y(x), (6*sin(x)/5 + 2*cos(x)/5)*exp(-x) + sin(x)/5 - 2*cos(x)/5)

例四：求下述微分方程的解：
$\begin{cases} \frac{\partial x_1}{\partial t}=2x_1-3x_2+3x_3,&x_1(0)=1,\\ \frac{\partial x_2}{\partial t}=4x_1-5x_2+3x_3,&x_2(0)=2,\\ \frac{\partial x_3}{\partial t}=4x_1-4x_2+2x_3,&x_3(0)=3. \end{cases}$

# coding=utf-8
# 求微分方程（方程组）的符号解：例四
# Copyright  源仔
# Crated：2021-08-25

import sympy as sp

t = sp.symbols('t')
x1,x2,x3 = sp.symbols('x1,x2,x3', cls=sp.Function)
eq = [x1(t).diff(t)-2*x1(t)+3*x2(t)-3*x3(t),
      x2(t).diff(t)-4*x1(t)+5*x2(t)-3*x3(t),
      x3(t).diff(t)-4*x1(t)+4*x2(t)-2*x3(t),
      ]
con = {x1(0):1, x2(0):2, x3(0):3}
s = sp.dsolve(eq,ics=con)
print(s)

或编辑如下简介的程序：
````python
# coding=utf-8
# 求微分方程（方程组）的符号解：例四
# Copyright  源仔
# Crated：2021-08-25

import sympy as sp

t = sp.symbols('t')
x1,x2,x3 = sp.symbols('x1:4',cls=sp.Function)
x = sp.Matrix([x1(t),x2(t),x3(t)])
A = sp.Matrix([[2,-3,3],[4,-5,3],[4,-4,2]])
eq = x.diff(t) - A*x
s = sp.dsolve(eq,ics={x1(0):1,x2(0):2,x3(0):3})
print(s)

OUT:

	[Eq(x1(t), 2*exp(2*t) - exp(-t)), Eq(x2(t), 2*exp(2*t) - exp(-t) + exp(-2*t)), Eq(x3(t), 2*exp(2*t) + exp(-2*t))]

1.2 数值解法

Python对常微分程的数值求解是基于一介方程进行的、告诫微分方程必须化成一介方程组，通常采用龙格—-库塔方法。scipy.integrate 模块的 odient 函数求常微分方程的数值解，其基本调用格式为：

sol = odeint(func, y0, t)

其中 function是定义微分方程的函数或匿名函数， y0 是初始条件的序列， t是一个自变量取值的序列（t 的第一个元素一定是初始时刻），返回值 sol 是对应于序列 t 中元素的数值解，如果微分方程组中有 n 个函数，返回值 sol 是 n 列的矩阵呢个，第i(i = 1,2,··· ，n) 列对应第 i 个函数的数值解。
例5：求微分方程
$\begin{cases} \frac{\partial y}{\partial x}=-2y+x^2+2x,\\ y(1)=2.\\ \end{cases}$
在0 $\le$ x$\le$10 步长间隔为 0.5 点上的数值解。

# coding=utf-8
# 求微分方程（方程组）的数值解：例五
# Copyright  源仔
# Crated：2021-08-26

from scipy.integrate import odeint
import numpy as np

dy = lambda y, x: -2*y+x**2+2*x
x = np.arange(1, 10.5, 0.5)
sol = odeint(dy, 2, x)
print("x+{}\n对应的数值解y={}".format(x, sol.T))# T表示转置

OUT:
x+[ 1.   1.5  2.   2.5  3.   3.5  4.   4.5  5.   5.5  6.   6.5  7.   7.5
  8.   8.5  9.   9.5 10. ]
对应的数值解y=[[ 2.          2.08484933  2.9191691   4.18723381  5.77289452  7.63342241
   9.75309843 12.12613985 14.75041934 17.62515427 20.75005673 24.12502089
  27.7500077  31.62500278 35.75000104 40.1250004  44.75000015 49.62500006
  54.75000002]]

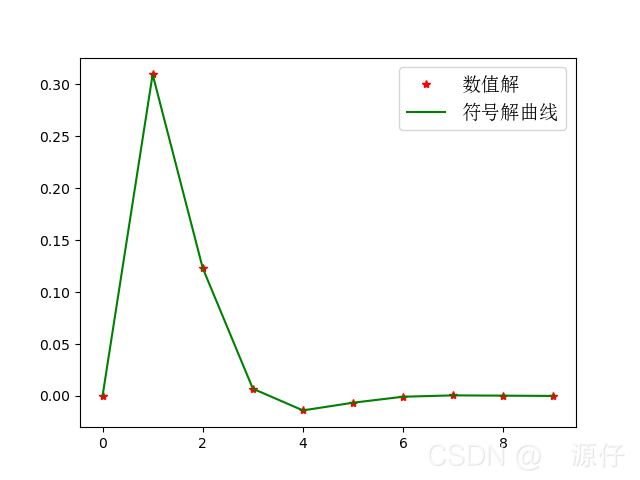
例六：求下述微分方程的数值解，并在同一个图形界面上画出符号姐和数值解的曲线
$\begin{cases} \frac{\partial^2 y}{\partial x^2}+2\frac{\partial y}{\partial x}+2y =0,&\\ y(0) = 0, \frac{\partial y}{\partial x}|_{x=0}=1. \end{cases}$

# coding=utf-8
# 求微分方程（方程组）的数值解：例六
# Copyright  源仔
# Crated：2021-08-26

from matplotlib.font_manager import FontProperties
from scipy.integrate import odeint
from sympy.abc import t
import numpy as np
import matplotlib.pyplot as plt

my_font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)

def Pfun(y, x):
    y1,y2 = y;
    return np.array([y2, -2*y1-2*y2])
x = np.arange(0, 10, 1.0)              # 创建时间点
sol1 = odeint(Pfun, [0.0, 1.0], x)     # 求数值解

plt.plot(x, sol1[:, 0],'r*',label="数值解")
plt.plot(x, np.exp(-x)*np.sin(x),'g', label="符号解曲线")
plt.legend(prop=my_font)  # 表示添加图例，并且用特有的 prop=my_font
plt.savefig("例六")
plt.show()

在这里插入图片描述

1.1.2 Lorenz 模型的混沌效应

Lorenz 模型是由美国气象学家 Lorenz 在研究大气运动时，通过化简对流模型，只保留 3 个变量提出的一个完全确定性的一阶自治常微分方程组（埠显含时间变量），其方程为：
$\begin{cases} \dot x=\sigma(y-x),\\ \dot y=\rho x-y-xz,\\ \dot z=xy-\beta z \end{cases}$
其中，参数 $\sigma$ 为 Prandtl 数， $\rho$ 为 Rayleigh 数， $\beta$ 为方向比。Lorenz 模型如今已经成为混沌领域的经典模型，第一个混沌吸引子————Lorenz 吸引子也是在这个系统中发现的。系统中三个参数的选择对系统会不会进入混沌状态其重要的作用。
下面左侧的图给出了 Lorenz 模型在 $\sigma$ =10， $\rho$ =28， $\beta$ = ${3\over 8}$ 时系统的三位演化轨迹。由此图可见，经过长时间运行后，系统只在三维空间的一个优先区域运动，即在三维空间里的测度为0，并显示出我们经常听到的蝴蝶效应。
右侧图给出了系统从两个考的很近的初值出发（相差仅为 0.0001）后，接的偏差烟花曲线。随着时间的增大，可以看见两个解的差异越来越大，这正是动力学系统对处置敏感性的直观表现，由此可以判定此系统的这种状态为混沌态。混沌运动时确定性系统中存在随机性，他的运动轨道对初始条件十分敏感。

# coding=utf-8
# 求微分方程（方程组）的数值解：例五
# Copyright  源仔
# Crated：2021-08-26

from scipy.integrate import odeint
import numpy as np
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt

def lorenz(w, t):
    sigma=10; rho=28; beta=8/3
    x, y, z=w;
    return np.array([sigma*(y-x), rho*x-y-x*z, x*y-beta*z])
t = np.arange(0, 50, 0.01)         # 创建时间点
sol1 = odeint(lorenz, [0.0, 1.0, 0.0], t)
sol2 = odeint(lorenz, [0.0, 1.0001, 0.0], t)

ax1 = plt.subplot(121,projection='3d')
ax1.plot(sol1[:,0],sol1[:,1],sol1[:,2],'r')

ax1.set_xlabel('$x$')
ax1.set_ylabel('$y$')
ax1.set_zlabel('$z$')

ax2 = plt.subplot(122,projection='3d')
ax2.plot(sol1[:,0]-sol2[:,0],sol1[:,1]-sol2[:,1],sol1[:,2]-sol2[:,2],'g')

ax2.set_xlabel('$x$')
ax2.set_ylabel('$y$')
ax2.set_zlabel('$z$')

plt.savefig("Lorenz 模型的混沌效应", dpi=500)
plt.show()

print("sol1=",sol1,'\n\n',"sol1-sol2=",sol1-sol2)

在这里插入图片描述

（二）微分方程建模方法

建立微分方程木星一般可以分为三步：
（1）根据实际要求确定研究的量（自变量、未知函数、必要的参数等），并确定坐标系。
（2）找出这些量满足的基本规律。
（3）运用这些归路列出方程和定解条件。

2.1 按规律直接列方程

例：将某物体放置于空气中，在时刻 t = 0 测量得他的温度为 $u_0$ = 150
$C^。$ （ $C^。$ 指摄氏度），10 min后测量得它得温度为 $u_1$ = 100 $C^。$ .奥球建立此物体得温度 $u$ 和时间 $t$ 的关系，并计算 20min 后物体的物体的温度，其中假设空气的温度保持为 $\overline u$ =24 $C^。$

解牛顿冷却定律是温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的归规律：当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比，比例系数成为热传递系数。

假设该物体在时刻 $t$ 的温度为 $u$ = u(t),则由牛顿冷却定律，得到

（1）式 $\frac{\partial u}{\partial t}$ = -k(u- $\overline u$ ) ,

其中，k > 0,方程（1）就是物体冷却过程的数学模型。注意到 $\overline u$=24 $ 为常数，u-$\overline u$ > 0，可将方程（1）改写为：

（2）式 $\frac{\partial (u-24)}{\ (u-24)}$ = -k $\partial t$

再对（2）两边同时积分后得：

（3）式 $u$ = 24 + 126 $e^{-kt}$

把条件 t = 10， $u$ = $u_1$ = 100 带入（3）式，得 看k = ${1\over 10}$ln ${126\over 76}$ = 0.0506，
故此物体得温度 $u$ 和时间 他的关系为 $u$ = 24 + 126$e^{-0.0506t}$.20min 后物体的温度为69.8413 $C^。$。

程序如下：

# coding=utf-8
# 按规律直接列方程.py
# Copyright 源仔
# Crated：2021-08-23

import sympy as sp

sp.var('t, k')   # 定义符号变量 t， k
u = sp.var('u', cls = sp.Function)   #定义符号函数
eq = sp.diff(u(t), t) + k * (u(t) - 24)  # 定义方程
uu = sp.dsolve(eq, ics = {u(0): 150})  # 求微分方程的符号解
print(uu)
kk = sp.solve(uu, k)   # kk返回值是列表，可能有多个解
k0 = kk[0].subs({t: 10.0, u(t): 100.0})
print(kk, '\t' , k0)
'''
sub() 源码
        >>> from sympy import pi, exp, limit, oo
        >>> from sympy.abc import x, y
        >>> (1 + x*y).subs(x, pi)
        pi*y + 1
        >>> (1 + x*y).subs({x:pi, y:2})
        1 + 2*pi
        >>> (1 + x*y).subs([(x, pi), (y, 2)])
        1 + 2*pi
        >>> reps = [(y, x**2), (x, 2)]
        >>> (x + y).subs(reps)
        6
        >>> (x + y).subs(reversed(reps))
        x**2 + 2

        >>> (x**2 + x**4).subs(x**2, y)
        y**2 + y
'''
u1 = uu.args[1]   # 提出符号表达式
u0 = u1.subs({t: 20, k: k0})  # 带入具体值
print("20分钟后的温度为： ", u0)

OUT:
Eq(u(t), 24 + 126*exp(-k*t))
[log(126/(u(t) - 24))/t] 	 0.0505548566665147
20分钟后的温度为：  69.8412698412698

2.2 微元分析法

该方法的基本思想是通过分析研究对象的有关变量再一个很短时间内的变化规律，寻找一些微元之间的关系式。
例：有高为 1m 的半球形容器，水葱它的底部小孔流出。小孔横截面积为 1 $cm^2$ 。开始时容器内盛满了水，求谁从小孔流出过程中容器里水面的高度 $h$ (水面与孔口中心的距离)随时间 $t$ 变化的规律。
解：如下图所示，以底部中心为坐标原点，垂直向上为坐标轴的正向建立坐标系。
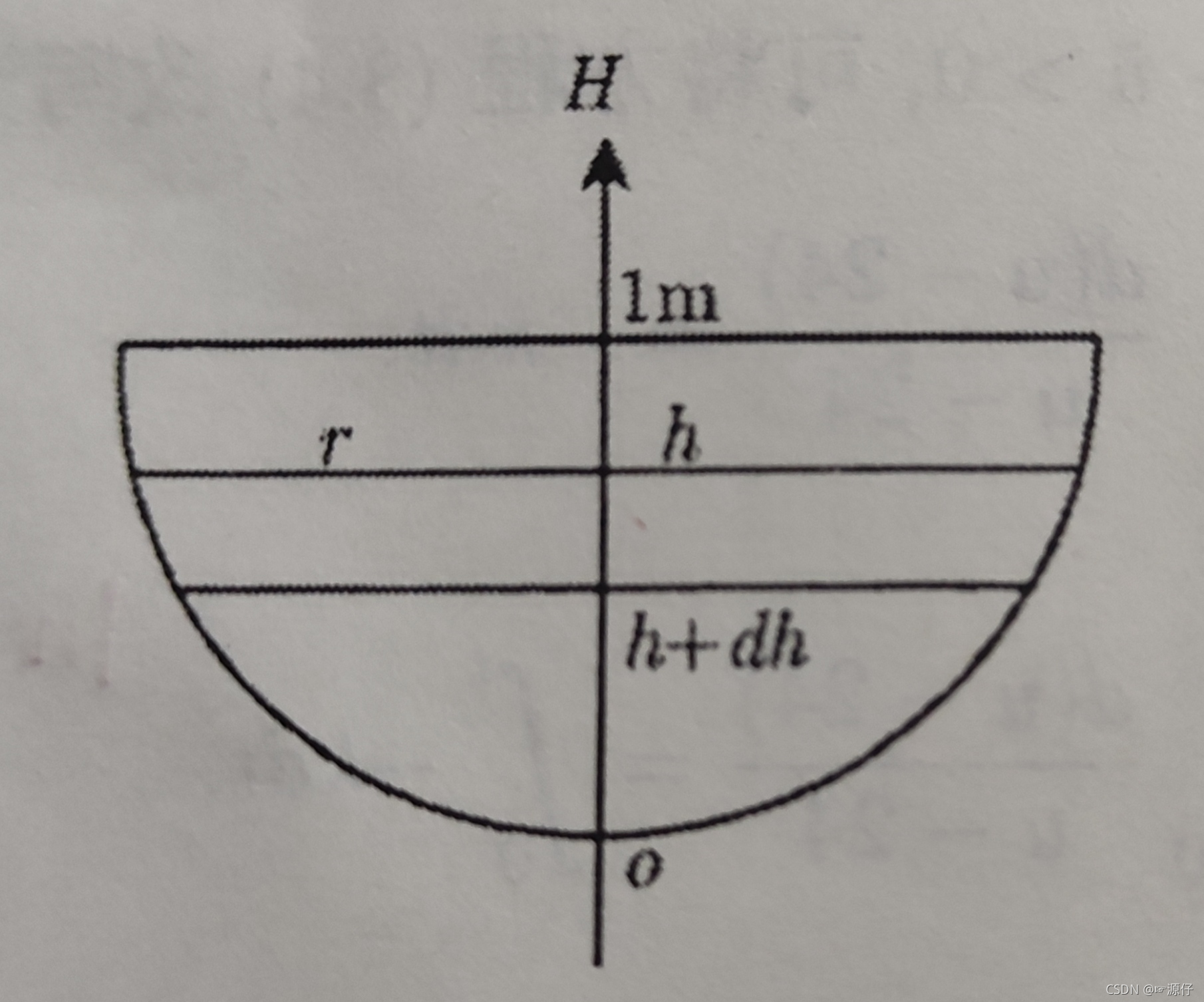
在这里插入图片描述

有水力学知，水从空口流出的流量 Q 为“通过空口横截面积的水的体积 V 对时间变化率”，满足：
（一式）Q = $\frac{\partial V}{\partial t}$ = 0.62S $\sqrt {2gh}$

（一式）中，0.62为流量系数：g 为重力加速度（取9.8 m/ $s^2$ ）,S为孔口横截面积（单位： $m^2$ ）,h 为 t 时刻水面高度（单位：cm）。当 S= 1 $cm^2$ = 0.0001 $m^2$ ,
（二式） dV = 0.000062 $\sqrt{2gh}$ dt

在微小时间间隔 [t, t+dt] 内，水面高度有 h 降到 h+dh （这里dh < 0），容器中谁的体积改变量近似为：
（三式）dV = - $\pi r^2dh$
（三式）中， $r$ 为 $t$ 时刻水面的半径，右端置负号式由于 dh < 0 ，而 dV > 0,这里
（四式） $r^2$ = [ $1^2$ - $1-h)^2$ ]=2 $h$ - $h^2$
由（二式）减（四式），得：
（五式） 0.000062 $\sqrt{2gh}$ dt= $\pi (h^2-2h)dh$
在考虑初值条件，得到如下的微分方程模型：
$\begin{cases} \frac{\partial t}{\partial h}={1000 \pi\over 0.62 \sqrt{2g}}(h^{3 \over 2}-2h^{1 \over 2}), \\ t(1) = 0. \end{cases}$
利用分离变量法，可以球的微分方程的解为:
$-15260.5042h^{3 \over 2} + 4578.1513h^{5 \over 2} + 10682.3530$
代码如下：

# coding=utf-8
# 微元分析法.py
# Copyright  源仔
# Crated：2021-08-23

import sympy as sp

sp.var('h')   # 定义符号变量
sp.var('t', cls = sp.Function) # 定义符号函数
g = 9.8
eq = t(h).diff(h) - 10000 * sp.pi/0.62/sp.sqrt(2*g) * (h**(3/2)-2*h**(1/2))  # 定义方程
t = sp.dsolve(eq, ics={t(1): 0})   # 求解微分方程的符号解
print(t)

t = sp.simplify(t)
print(t.args[1].n(9))
'''
simplify() 源码
    >>> from sympy import simplify, cos, sin
    >>> from sympy.abc import x, y
    >>> a = (x + x**2)/(x*sin(y)**2 + x*cos(y)**2)
    >>> a
    (x**2 + x)/(x*sin(y)**2 + x*cos(y)**2)
    >>> simplify(a)
    x + 1
args() 源码   
    def args(self):
        """Returns a tuple of arguments of 'self'.

        Examples
        ========

        >>> from sympy import cot
        >>> from sympy.abc import x, y

        >>> cot(x).args
        (x,)

        >>> cot(x).args[0]
        x

        >>> (x*y).args
        (x, y)

        >>> (x*y).args[1]
        y

        Notes
        =====

        Never use self._args, always use self.args.
        Only use _args in __new__ when creating a new function.
        Don't override .args() from Basic (so that it's easy to
        change the interface in the future if needed).
        """
        return self._args
'''

OUT:
Eq(t(h), 45539712848047*pi*sqrt(h)*(2*h + 3*(h - 2)**2 - 12)/93750000000 + 318777989936329*pi/93750000000)
-15260.5042*h**1.5 + 4578.15127*h**2.5 + 10682.353

2.3 模型近似法

该方法得基本思想是在不同得假设下模拟实际的现象，即建立模拟近似得微分方程。从数学上求解或分析接的性质，再去和实际情况做对比，观察这个模型能否模拟，近似某些实际的现象。

例：（交通管理问题）在交叉的十字路口，都会设置红绿灯。为了让那些正常行驶在交叉路口或离交叉路口太近无法停下的车辆通过路口，红绿灯转换中间还要两栖一段时间的黄灯。那么，黄灯应该亮多长时间才合适呢？

分析 黄灯状态持续的时间包括驾驶员的反应时间、车通过交叉路口的时间以及通过刹车距离所需要的时间。

解： 记 $v_0$ 式法定速度， $I$ 是交通路口的长度，则车通过路口的时间为 $\over v_0$

下面计算刹车距离，刹车距离就是从开始刹车到速度 $v = 0$ 时汽车通过的距离。设 $W$ 为汽车的重量， $u$ 为摩擦系数。显然，地面对汽车的摩擦力为 $u W$ ，其方向与运动方向想法。由牛顿第二定律，汽车在停止过程中，形式的距离 $x$ 与时间 $t$ 的谷氨醯可由如下微分方程表示：
（一）式： $\over g$ · $d^2x \over dt^2$ = - $u W$
其中， $g$ 为重力加速度，化简为：
（二）式： $d^2x \over dt^2$ = - $u g$
再考虑初值条件，建立如下微分方程模型：
$\begin{cases} {d^2x \over dt^2}= -ug,\\ x|_{t=0}=0, {dx \over dt}|_{t=0}=v_0. \end{cases}$
求得解为：
（四）式： $x (t)$ =- $\over 2$ $ugt^2$ + $v_0t$
令 $\over dt$ =0，可得刹所用的时间 $t_0$ = $v_0 \over ug$ ，从而得到刹车距离 $x(t_0)$ = $v_0^2 \over 2ug$ 。

2.下面计算黄灯状态的时间 T ，则；
（五）式： $T$ = ${x(t_0)+I+L} \over v_0$ + $T_0$
其中 $T_0$ 是驾驶员的反应时间，代入 $x(t_0)$ 得：
（六）式： $T$ = $v_0 \over 2ug$ + $\over v_0$ + $T_0$
设 $T_0$ = 1s， $L$ = 4.5m， $I$ = 9m.另外，取具体代表性的 $u = 0.7$ ，当 $v_0$ = 45km/h、65km/h以及 80km/h 时，黄灯时间 $T$ 如下表所示：

表：不同速度下计算的黄灯时长
$v_0$	45	65	80
$\over s$	4.58	5.95	7.00

程序如下：

# coding=utf-8
# 计算黄灯时间的 python程序
# Copyright  源仔
# Crated：2021-08-28

from numpy import array

v0 = array([45, 65, 80])
T0 = 1; L = 4.5; I = 9; mu = 0.7; g = 9.8
T = v0/(2*mu*g)+(I+L)/v0+T0

print(T)