[Python知识库]数学建模算法与应用——用python进行程序的编写

第1章 线性规划

化成matlab后使用python进行求解：
首先需要导入numpy与scipy模块
调用scipy中的optimize.linprog即可

#optimize.linprog的使用方法大致如下
result = optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
            bounds=None, method='interior-point', callback=None,
            options=None, x0=None)
# c : 1-D array       A_ub : 2-D array          b_ub : 1-D array          A_eq : 2-D array     b_eq : 1-D array
#bounds=((min,max),(min,max)~)          (min, max)`` pairs for each element in ``x``

from scipy import optimize
import numpy as np

f=np.transpose(np.array([-2,-3,5]))
a=np.array([[-2,5,-1],[1,3,1]])
b=np.array([-10,12])
Aeq=np.array([[1,1,1]])
beq=np.array([7])
res = optimize.linprog(f, a, b, Aeq, beq, bounds=((0,None),(0,None),(0,None)))
print(res)

f=np.transpose(np.array([2,3,1]))
a=np.array([[1,4,2],[1,2,0]])
b=np.array([8,6])
res = optimize.linprog(f, a, b, bounds=((0,None),(0,None),(0,None)))
print(res)

第2章 整数规划

生成1000*1000个点，计算每个点符合区域：

    x=np.arange(0,12,step=12/1000)
    y=np.arange(0,9,step=9/1000)

    t=0
    for xx in x:
        for yy in y:
            if yy<12-xx and yy<xx**2:
                t+=1
    print(t)
    area_appr=12*9*t/1000000
    print(area_appr)

计算的结果为49.550508

import numpy as np
#采用统计随机点落在曲边三角形的频数
x=np.random.uniform(0,12,10**7)
y=np.random.uniform(0,9,10**7)
z1=np.where(x<=3,(y-x**2)<0,False)
z2=np.where(x>=3,(12-x)>y,False)
z3=((z1==True).sum())+((z2==True).sum())#总频数
print(12*9*z3/10**7)

结果为：49.5045648

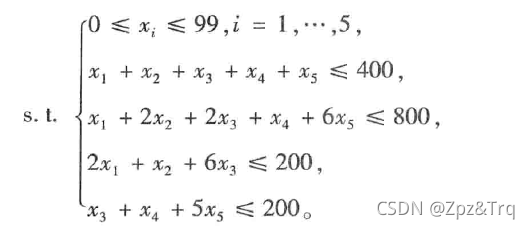
import numpy as np
import random

x=np.random.randint(0,100,size=(5))
print(x)
def fun_f(x):
    a=x[0]**2+x[1]**2+3*x[2]**2+4*x[3]**2+2*x[4]**2
    b=-8*x[0]-2*x[1]-3*x[2]-x[3]-2*x[4]
    return a+b

def fun_g(y):
    a=y[0]+y[1]+y[2]+y[3]+y[4]-400
    b=y[0]+2*y[1]+2*y[2]+y[3]+6*y[4]-800
    c=2*y[0]+y[1]+6*y[2]-200
    d=y[2]+y[3]+5*y[4]-200
    return np.array([a,b,c,d])

chushi=fun_f(x)
end=x
i=0
while i<10**6:
    globals()
    x=np.random.randint(0,100,size=(5))
    y=fun_f(x)
    judge=all(fun_g(x)<0)
    if judge:
        res=fun_f(x)
        if res>chushi:
            end=x
    else:
        continue
    i+=1
#    if i%10**4==0:
#        print(i)

print(end)
print(fun_f(end))

每次的结果有些差异：

#第一次
[35 98  1 97 13]
48204
#第二次
[35 55  3 72 12]
24806