Kalman滤波

状态估计器
模型精确和随机干扰信号统计特性已知的线性系统
本质：贝叶斯模型 + 最小均方误差估计
步骤
- 根据上一次的最优状态估计和最优估计误差去计算这次的先验状态估计和先验误差估计
- 根据本次先验误差估计和测量噪声，得到卡尔曼增益
- 根据当前测量值和先验状态估计值，通过卡尔曼增益加权，得到本次的最优估计

推导

五个公式

预测

$\hat{x}_k^- = F_k \hat{x}_{k-1} + B_k\vec{u}_k$

$P_k^- = F_k P_{k-1}F_k^T + Q_k$

更新

$K_k = P_k^- H_k^T(H_kP_k^-H_k^T + R_k)^{-1}$

$\hat{x}_k = \hat{x}_k^- + K_k (\vec{z}_k - H_k \hat{x}_k^-)$

$P_k = P_k^- - K_kH_kP_k^-$

参数	含义
$\hat{x}_k^-$	k时刻的先验状态估计值，根据k-1时刻的最优估计预测的k时刻的结果
$P_k^-$	k时刻的先验估计协方差，预测状态不确定性度量
$\hat{x}_k$	k时刻的后验状态估计值，最优估计
$P_k$	k时刻的后验估计协方差
$R_k$	观测噪声协方差矩阵
$H_k$	观测矩阵
$K_k$	卡尔曼增益
$B_k$	控制矩阵，控制向量如何作用当前矩阵
$\vec{u}_k$	控制向量
$F_k$	状态转移矩阵，如何从上一状态推测当前状态
$\vec{z}_k$	k时刻观测值
$Q_k$	过程噪声协方差矩阵

推导过程

先列出状态预测方程

$x_k = F_kx_{k-1}+B_ku_k + w_{k-1}$

利用预测状态的协方差矩阵描述不确定度

$P_k = cov(x_k, x_k)=cov(F_kx_{k-1}) + cov(B_ku_k) + cov(w_k) \\ =F_kP_{k-1}F_k^T +Q_k$

实际过程中，状态元素有时候无法直接测量，需要观测方程实现状态转移

$z_k = H *x_k+v_k$

真实值与预测值误差

$e_k^- = x_k - x_k^-\\$

真实值与预测值误差协方差为

$P_k^- = E(e_k^- * e_k^{-T})$

真实值与估计值误差

$e_k = x_k - \hat{x}_k = x_k - (\hat{x}_k^- + K_k (\vec{z}_k - H_k \hat{x}_k^-)) \\ =(I-K_kH_k)(x_k-x_k^-) - K_kv_k$

真实值与估计值误差的协方差为

$P_k = E(e_k*e_k^T) \\ = E([(I-K_kH_k)(x_k-x_k^-) - K_kv_k][(I-K_kH_k^T)(x_k-x_k^-) - K_kv_k]^T) \\ = (I-K_kH_k)P_k^-(I-K_kH_k)^T + K_kRK^T \\ = P_k^- - K_kH_kP_k^- - P_k^-H_k^T + K_k(H_kP_k^-H^T + R)K_k^T$

卡尔曼滤波的估计原则就是使最优状态估计的协方差 $P_k$ 最小
$P_k$ 对卡尔曼增益矩阵 $K$ 求偏导

$\frac{?P_k}{?K_k} = -2(P_k^-H^T) + 2K_k(H_kP_k^-H^T + R) = 0$

求得卡尔曼增益 $K_k$ 为

$K_k = P_k^-H_k^T(H_kP_k^-H^T + R)^{-1}$

将 $K_k$ 代入 $P_k$ ，得到

$P_k = P_k^- - K_kH_kP_k^-$

实现

卡尔曼滤波的预测、更新车辆轨迹
根据已知轨迹，预测后面多步的轨迹
分别使用cv2.KalmanFilter和按照上述公式推导实现
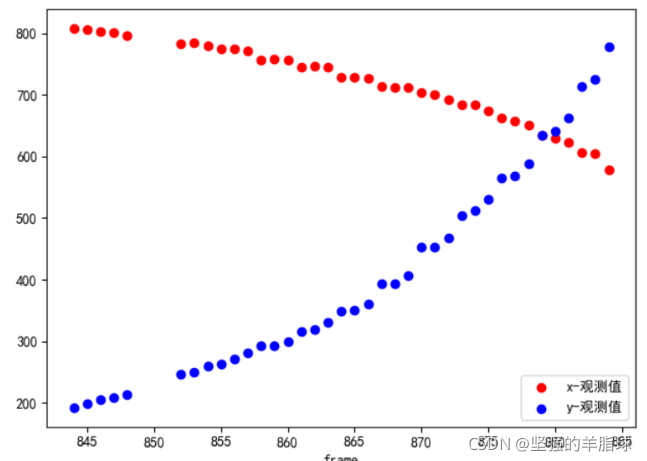
数据使用视频帧号和目标对应中心点的x和y坐标

cv2.KalmanFilter

cv2.KalmanFilter函数介绍如下

cv2.KalmanFilter(dynam_params, measure_param, control_params) # 创建kalman滤波器 
    dynam_params：状态空间的维数； 4
    measure_param：测量值的维数；  2
    control_params：控制向量的维数，默认为0。由于这里该模型中并没有控制变量，因此也为0。
kalman.measurementMatrix 观测矩阵 H
kalman.transitionMatrix  状态转移矩阵 F
kalman.processNoiseCov 处理噪声协方差矩阵  Q
kalman.measurementNoiseCov 观测噪声协方差矩阵 R
kalman.controlMatrix 控制矩阵 B
kalman.statePost   校正状态 
kalman.statePre   预测状态
kalman.errorCovPost 后验方差协方差阵 P = (I-KH)P'(k)
kalman.errorCovPre 先验方差
kalman.gain 卡尔曼增益矩阵

实现如下

# 状态量  x, y, Vx, Vy
kalman = cv2.KalmanFilter(4, 2)
kalman.measurementMatrix = np.array([[1, 0, 0, 0], [0, 1, 0, 0]], np.float32) # 设置测量矩阵 H
kalman.processNoiseCov = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]], np.float32) # 设置过程噪声协方差矩阵 Q
kalman.measurementNoiseCov = np.matrix([[1, 0], [0, 1]])    # 观测噪声方差

num = len(info['frame'])
for k in range(1, num):
    delt = (info['frame'][k] - info['frame'][k-1])
    kalman.transitionMatrix = np.array([[1, 0, delt, 0], [0, 1, 0, delt], [0, 0, 1, 0], [0, 0, 0, 1]], np.float32) # 设置转移矩阵 F

    x, y = info['x'][k], info['y'][k]
    current_measurement = np.array([[np.float32(x)], [np.float32(y)]])
    kalman.correct(current_measurement)  # 用当前测量来校正卡尔曼滤波器
    current_prediction = kalman.predict()
    plt.scatter(info['frame'][k], current_prediction[0][0], color='g')
    plt.scatter(info['frame'][k], current_prediction[1][0], color='y')
plt.show()

自己实现

    x_hat = np.matrix([[info['x'][0]], [info['y'][0]], [0], [0]])
    P = np.matrix(np.diag([1, 1, 1, 1]))
    Q = np.matrix(np.diag([1, 1, 1, 1]))
    # Q = np.matrix([[1/3, 0, 1/2, 0], [0, 1/3, 0, 1/2], [1/2, 0, 1, 0], [0, 1/2, 0, 1]], np.float32)
    H = np.matrix([[1, 0, 0, 0], [0, 1, 0, 0]])
    R = np.matrix([[1, 0], [0, 1]])
    figure = plt.figure()
    plt.scatter(info['frame'], info['x'], color='r', label='x-观测值')
    plt.scatter(info['frame'], info['y'], color='g', label='y-观测值')

    for k in range(1, num):
        delt_t = (info['frame'][k] - info['frame'][k - 1])
        F = np.matrix([[1, 0, delt_t, 0], [0, 1, 0, delt_t], [0, 0, 1, 0], [0, 0, 0, 1]])
        # 预测
        x_hat_minus = F * x_hat
        P_minus = F * P * F.T + Q

        # 更新
        K = P_minus * H.T * np.linalg.inv(H * P_minus * H.T + R)
        x_hat = x_hat_minus + K * (np.matrix([[info['x'][k]], [info['y'][k]]]) - H * x_hat_minus)
        P = P_minus - K * H * P_minus

        plt.scatter(info['frame'][k], x_hat_minus.A[0][0], color='olive', label='x-预测值', marker='s')
        plt.scatter(info['frame'][k], x_hat_minus.A[1][0], color='pink', label='y-预测值', marker='*')
    plt.show()

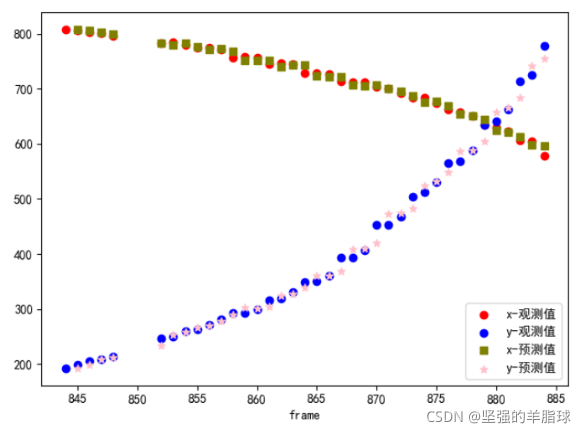
轨迹预测

通过修改delt_t，实现之后轨迹的预测
因为没有观测值的加权，导致预测值会有部分误差

# 往后预测10步
for i in range(1, 11):
# 多步预测
delt_t = i
F = np.matrix([[1, 0, delt_t, 0], [0, 1, 0, delt_t], [0, 0, 1, 0], [0, 0, 0, 1]])
x_hat_minus = F * x_hat