[Python知识库]python数据拟合

python数据拟合

1.多项式拟合

1.1 多项式拟合描述

输入：多项式次数$n$；数据集合 { ( x i , y i ) } \{(x_i,y_i)\} {(xi?,yi?)}
输出：$f_n(x)$，使得 $\sum (f(x_i)?y_i{)}^2$ 最小

解决方案：polyfit ( x , y , deg , rcond = None , full = False , w = None )

1.2 多项式拟合实现

导入库：numoy、matplotlib

#导入库
import numpy as np
import matplotlib.pyplot as plt

生成测试数据：

#定义测试多项式函数
def func1(x):
    return 3*x*x*x-2*x*x+4

#生成测试数组
x1 = np.array([1,2,3,4,5,6,7,8])
y1 = func1(x1)

#添加噪声
n1 = np.random.normal(0.0,1.0,8)*0.1
y1 = y1*(1+n1)

数据拟合：

f1 = np.polyfit(x1, y1, 3)
p1 = np.poly1d(f1)
print('p1 is :\n',p1)

p1 is :
3 2
-1.897 x + 57.77 x - 204.8 x + 177.6

得到拟合函数：
$f_1=?1.897x^3+57.77x^2?204.8x+177.6$

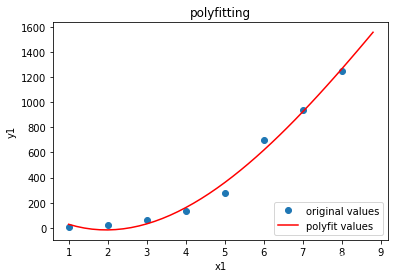
绘制拟合曲线：

xx1 = np.arange(1,9,0.2)
yvals1 = p1(xx1) #拟合y值

#绘图
plot1 = plt.plot(x1, y1, 'o',label='original values')
plot2 = plt.plot(xx1, yvals1, 'r-',label='polyfit values')
plt.xlabel('x1')
plt.ylabel('y1')
plt.legend(loc=4) #指定legend的位置右下角
plt.title('polyfitting')
plt.show()

2.自定义函数拟合

2.1 自定义函数拟合描述

输入：自定义函数$f(x)$及参数${\sigma }_i$；数据集合 { ( x i , y i ) } \{(x_i,y_i)\} {(xi?,yi?)}
输出：使得 $\sum (f(x_i)?y_i{)}^2$ 最小参数取值

解决方案：scipy.optimize.curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=True, bounds=(- inf, inf), method=None, jac=None, **kwargs)

2.1 自定义函数拟合的实现

导入库：numpy、matplotlib、scipy

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

设置拟合数据：

x2 = np.array([1,2,3,4,5,6,7,8,9,10])
y2 = np.array([0.16,0.63,1.60,3.00,8.00,33.0,73.0,125.0,211.0,310.0])
y2=y2*100

自定义拟合函数：

def func2(x, p, q,m):
    return m*(1-np.exp(-x*(p+q)))/(1+q/p*np.exp(-(p+q)*x))

非线性最小二乘法拟合：

popt, pcov = curve_fit(func2, x2, y2)

拟合y值

p = popt[0] 
q = popt[1]
m = popt[2]

yvals2 = func2(x2,p,q,m) #拟合y值
print('popt:', popt)
print('系数p:', p)
print('系数q:', q)
print('系数m:', m)
print('系数pcov:', pcov)
print('系数yvals2:', yvals2)

popt: [4.93963593e-04 7.86873973e-01 4.96871803e+04]
系数p: 0.0004939635925128215
系数q: 0.7868739729224568
系数m: 49687.18030400891
系数pcov: [[ 1.16165013e-08 -4.88182871e-06 3.60534694e-01]
[-4.88182871e-06 2.28100736e-03 -1.95238501e+02]
[ 3.60534694e-01 -1.95238501e+02 1.97747550e+07]]
系数yvals2: [ 37.30343602 119.0851606 297.86586198 686.25958059
1518.69723981 3252.26832861 6655.68174484 12625.30614774
21284.37699301 30920.18607139]

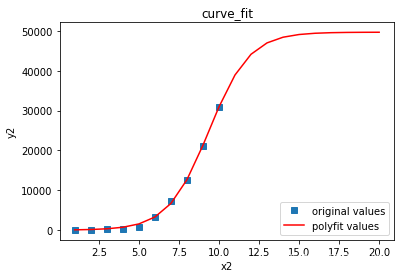
绘制拟合图像

xx2 = np.arange(1,21)
y2test = func2(xx2,p,q,m)

#绘图
plot1 = plt.plot(x2, y2, 's',label='original values')
plot2 = plt.plot(xx2, y2test, 'r',label='polyfit values')
plt.xlabel('x2')
plt.ylabel('y2')
plt.legend(loc=4) #指定legend的位置右下角
plt.title('curve_fit')
plt.show()