[Python知识库]numpy基础用法

入门numpy

基础操作

import numpy

data = numpy.array([1, 2, 3])

data.max()
print(data.max()) #实现求max
numpy.ones(3)
print(numpy.ones(3)) # 赋值为1
numpy.zeros(3)
print(numpy.zeros(3)) # 赋值为0
numpy.random.random(3) 
print(numpy.rabdom.random(3)) # 生成3列的浮点数，浮点数都是从0-1中随机

输出结果为：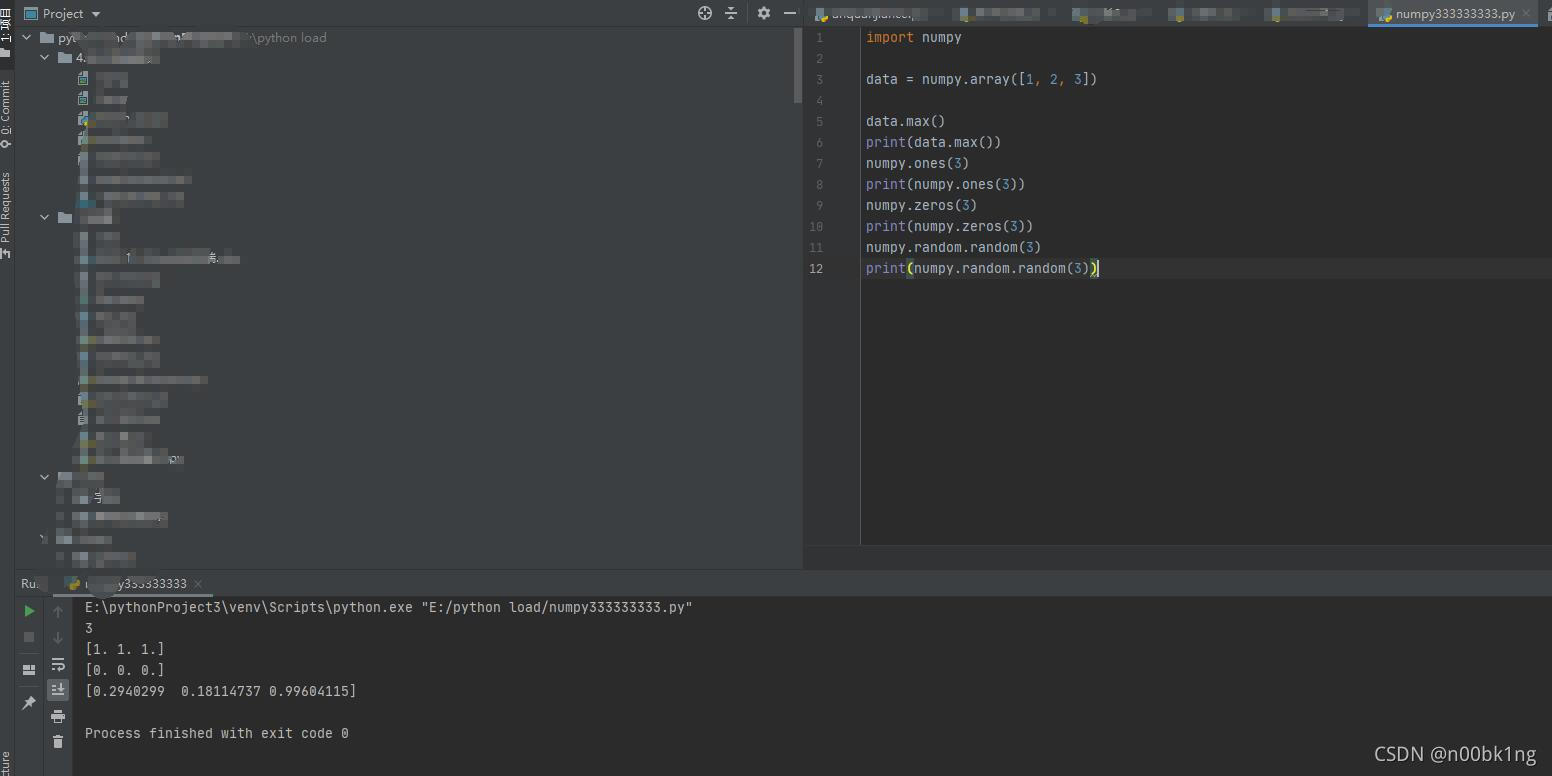

import numpy

data = numpy.array([1, 2])
ones = numpy.ones(2)

print(data + ones)  # 加法
print(data - ones)  # 减法
print(data * data)  # 乘法
print(data / data)  # 除法
print(data * 1.6)   # 与常数的乘法

输出结果：

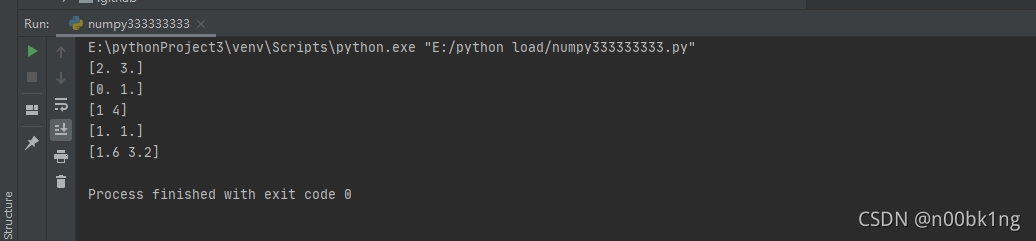
聚合函数

import numpy

data = numpy.array([1, 2, 3, 4])
print(data[0])  # 输出数组第一个元素
print(data[1])  # 输出数组第二个元素
print(data[0:2])  # 输出数组第1,2个元素
print(data[1:])  # 输出数组第1个元素后的元素
print(data.max())  # 输出max值
print(data.min())  # 输出min值
print(data.sum())  # 输出总和
print(numpy.ones((3, 2)))  # 生成三行二列的1
print(numpy.zeros((3, 2)))  # 生成三行二列的0
print(numpy.random.random((3, 2)))  # 生成3行2列的浮点数，浮点数都是从0-1中随机,维度：2

实现结果：

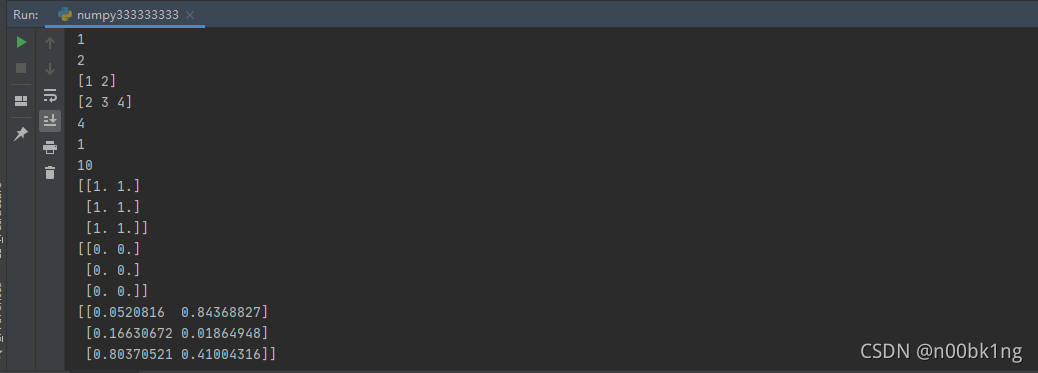
利用（配合高维）

import numpy

data = numpy.array([[1, 2], [3, 4], [5, 6]])
print(data.max(axis=0))  # 找每一列中最大的数，并求和
print(data.max(axis=1))  # 找每一行中最大的数，并求和
data1 = numpy.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])  # 高维数组
print(data1)

实现结果：

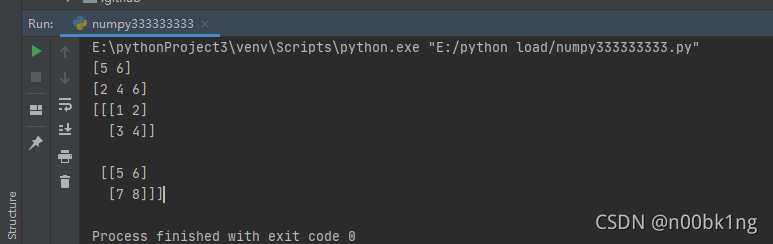
具体操作

数组拆分

垂直拆分：numpy.vsplit(数组，份数)->(数组片段)

import numpy

x = numpy.arange(1, 13).reshape(6, 2)
print(x)
y = numpy.vsplit(x, 3)
print(y)

实现结果：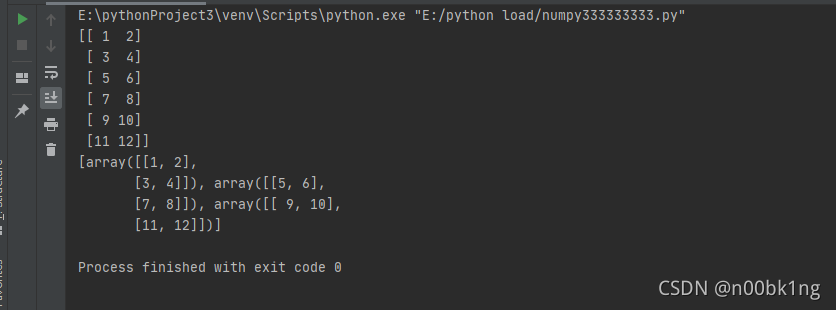
水平拆分：numpy.hsplit(数组，份数)->(数组片段)

import numpy

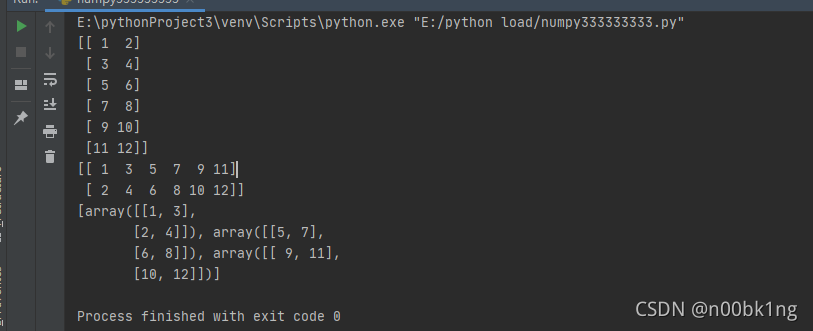
x = numpy.arange(1, 13).reshape(6, 2)
print(x)
# y = numpy.vsplit(x, 3)
# print(y)
z = x.T
print(z)
zz = numpy.hsplit(z, 3)
print(zz)

实现结果：

numpy.dsplit(数组，份数)->(数组片段)

  In [32]: e = np.dstack((a,b))    
  In [33]: e Out[33]:  array([[[11, 21],
             [12, 22],
             [13, 23]],

   [[14, 24],
    [15, 25],
    [16, 26]],

   [[17, 27],
    [18, 28],
    [19, 29]]])   In [35]: np.dsplit(e,2) Out[35]:  [array([[[11],
     [12],
     [13]],

    [[14],
     [15],
     [16]],

    [[17],
     [18],
     [19]]]), array([[[21],
     [22],
     [23]],

    [[24],
     [25],
     [26]],

    [[27],
     [28],
     [29]]])]

灵活选择引用

inistate =np.array([1,2,3,4])
pre_inistate = inistate[0:3]
pre_inistate

array([0.18257419, 0.36514837, 0.54772256])

numpy基本加减和取行操作
矩阵删除、插入、尾部添加操作(delete,insert,append)
delete()函数
insert()函数
append()函数
np.random.choice(a, size, replace, p)
np.argmax(a, axis=None, out=None)
星号()的作用
ndarray.ndim代表的就是shape元组的长度。
numpy.linspace用法
拉平操作 ravel()和faltten()及reshape(1,-1)的区别联系(补充[None,:]操作)
np.prod() 计算元素乘积
把矩阵大于或小于N的元素置M的技巧
numpy中的矩阵copy问题
np.zeros_like()构造全零矩阵，无需指定大小
random.rand和random.rand和random.randint区别
np.random.random() 生成一个随机数
np.random.uniform()
np.random.rand() 生成均匀分布矩阵
np.random.randn() 生成正太分布矩阵
np.randm.randint() 生成离散均匀分布的整数值组成的矩阵
python 断言 assert
星号( * ) 和 .dot 和 np.multiply 的区别联系
np.pad()函数进行padding操作
numpy.empty() 创建指定形状和数据类型且未初始化的数组
判断两个矩阵元素完全相等&&存在相等
关于 np.mat() 的使用
np.full 用于形成元素全为某元素的矩阵
astype 转换数据类型
np.meshgrid() 快速生成网格
np.hstack() 和 np.vstack() 用于堆叠矩阵
numpy 取整
np.newaxis 在特定位置增加一个维度
python 广播机制
numpy.transpose()转置
numpy 中双冒号的用法

numpy基本加减和取行操作

    import numpy as np
    a = np.array([1,1,1,1])
    b = np.array([[1],[1],[1],[1]])
    a+b
    array([[2, 2, 2, 2],
    [2, 2, 2, 2],
    [2, 2, 2, 2],
    [2, 2, 2, 2]]) # 这叫python的广播机制

    c = np.array([[1,1,1,1]])
    c+b
    array([[2, 2, 2, 2],
    [2, 2, 2, 2],
    [2, 2, 2, 2],
    [2, 2, 2, 2]])
    W = np.array([[1,1,1],[2,2,2]])
    W[:,1]
    array([1, 2]) # 这里要特别注意，W[:,1]虽然取的是W的第一列，但是返回的却是一维数组

    W[1]
    array([2, 2, 2]) # 取得是W第一行，返回的也是一维数组

    W[:,1] = np.array([5,5])
    W
    array([[1, 5, 1],
    [2, 5, 2]]) # 这里用array[5,5]这样的一维数组直接可以把W矩阵的第1列替换(维度符合即可)

矩阵删除、插入、尾部添加操作(delete,insert,append)

numpy矩阵操作主要有delete()、insert()、append()等函数，分别执行删除、插入和添加的操作，注意append可以看为insert函数的特殊情况，即在尾部补充可以看为插入最后一行或列，这在后文会举例说明。

delete()函数

#numpy.delete(arr,obj,axis=None)
#axis 表明哪个维度的向量应该被移除
#axis 如果为None，则需要先将矩阵拉平，在删去第obj的元素
#obj 表明axis维度的哪一行(或列)应该被移除。

举例说明如下

import numpy as np  
matrix = [ [1,2,3,4], [5,6,7,8], [9,10,11,12] ]  
p1= np.delete(matrix, 1, 0) # 第0维度(行)第1行被删除(初始行为0行) 
print(’>>>>p1>>>>\n’,p1) p2 = np.delete(matrix, 1, 1) # 第1维度(列)第1行被删除 
print(’>>>>p2>>>>\n’,p2) p3 = np.delete(matrix, 1) #拉平后删除第1个元素(初始为第0个) 
print(’>>>>p3>>>>\n’,p3) p4 = np.delete(matrix,[0,1], 1) # 第1维度(列)第0、1行被删除 
print(’>>>>p4>>>>\n’,p4)

结果

        p1>>>>
        [[ 1 2 3 4]
        [ 9 10 11 12]]

        p2>>>>
        [[ 1 3 4]
        [ 5 7 8]
        [ 9 11 12]]

        p3>>>>
        [ 1 3 4 5 6 7 8 9 10 11 12]

        p4>>>>
        [[ 3 4]
        [ 7 8]
        [11 12]]

insert()函数

#numpy.insert(arr,obj,value,axis=None)
#value 为插入的数值
#arr 为目标向量
#obj 为目标向量的axis维度的目标位置
#axis 为想要插入的维

举例如下

import numpy as np
matrix = [
[1,2,3,4],
[5,6,7,8],
[9,10,11,12]
]
q1 = np.insert(matrix, 1, [1,1,1,1], 0) # 第0维度(行)第1行添加[1,1,1,1]
print(’>>>>q1>>>>\n’,q1)
q2 = np.insert(matrix, 0, [1,1,1], 1) # 第1维度(列)第0列添加1,1,1
print(’>>>>q2>>>>\n’,q2)
q3 = np.insert(matrix, 3, [1,1,1,1], 0) # 第0维度(行)第3行添加[1,1,1,1]
print(’>>>>q3>>>>\n’,q3)

结果

        q1>>>>
        [[ 1 2 3 4]
        [ 1 1 1 1]
        [ 5 6 7 8]
        [ 9 10 11 12]]

        q2>>>>
        [[ 1 1 2 3 4]
        [ 1 5 6 7 8]
        [ 1 9 10 11 12]]

        q3>>>>
        [[ 1 2 3 4]
        [ 5 6 7 8]
        [ 9 10 11 12]
        [ 1 1 1 1]]

append()函数

#numpy.append(arr,values,axis=None)
#将values插入到目标arr的最后，其中values与arr应该有相同维度，具体见例子

import numpy as np
matrix = [
[1,2,3,4],
[5,6,7,8],
[9,10,11,12]
]
m1 = np.append(matrix,[[1,1,1,1]],axis=0)  # 第0维度(行)尾部添加[[1,1,1,1]],注意两个[],相同维度

print(’>>>>m1>>>>\n’,m1)
m2 = np.append(matrix,[[1],[1],[1]],axis=1)  # 第1维度(列)尾部添加[[1],[1],[1]],注意两个[],相同维度

print(’>>>>m2>>>>\n’,m2)
m3 = np.append(matrix,[1,1,1,1])  # 拉平后再尾部添加[1,1,1,1]，这里可以[[1,1,1,1]]和[1,1,1,1]均可

print(’>>>>m3>>>>\n’,m3)

结果：

        m1>>>>
        [[ 1 2 3 4]
        [ 5 6 7 8]
        [ 9 10 11 12]
        [ 1 1 1 1]]

        m2>>>>
        [[ 1 2 3 4 1]
        [ 5 6 7 8 1]
        [ 9 10 11 12 1]]

        m3>>>>
        [ 1 2 3 4 5 6 7 8 9 10 11 12 1 1 1 1]

需要注意的是m1 = np.append(matrix,[[1,1,1,1]],axis=0) 与 q3 = np.insert(matrix, 3, [1,1,1,1], 0)结果一致，尾部添加即为最后行或列的插入操作。

np.random.choice(a, size, replace, p)

其作用是按要求生成一个一维数组
a是生成一维数组的来源，可以是int类型，可以是数组，也可以是list
size 数组的维度replace 表示从a中是否不重复抽取，默认可重复 p 给出抽取概率，默认随机
注意 ：这里是围绕数组展开的，如果提取的也是list，可以用 from random import choice 的 choice，可用 from random import sample 随机抽取一组元素

import numpy as np
a1 = np.random.choice(7,5) # 从0~7中随机选择5个数组成一维数组
a1
array([3, 1, 0, 1, 4])

a2 = np.random.choice([0,1,2,3,4,5,6],5) # 从给定list中随机选择5个数组成一维数组
a2
array([1, 6, 6, 6, 4])

a3 = np.random.choice(np.array([0,1,2,3,4,5,6]),5) # 将list换成array数组依然可以运行，效果一致
a3
array([3, 0, 5, 5, 3])

a4 = np.random.choice([0,1,2,3,4,5,6],5,replace=False) # 上述均有重复，将replace设置为False，即可按要求没有重复的选取
a4
array([0, 4, 3, 6, 5])

a5 = np.random.choice(np.array([0,1,2,3,4,5,6]),5,p=[0.1,0.1,0.1,0.1,0.1,0.1,0.4])

给出选取概率p，注意p的维度和a的维度一致，并且p中概率和为1

a5
array([6, 3, 2, 6, 6])

np.argmax(a, axis=None, out=None)

作用是返回轴的最大值的索引值
a：需要操作的数组或者矩阵，默认情况拉平成数组
axis：默认将a拉平，当axis=0对a按列取最大值索引，axis=1则对a按行取最大值索引
out：将结果写到a中

        import numpy as np
        a = np.array([[1,1,1],[2,2,2],[0,3,6]])
        a
        array([[1, 1, 1],
        [2, 2, 2],
        [0, 3, 6]])

        b1 = np.argmax(a) # 将数组a拉平，最大值索引为9(初始索引为0)
        b1
        8

        b2 = np.argmax(a, axis=0) # 按列选取最大值的索引
        b2
        array([1, 2, 2], dtype=int64)

        b3 = np.argmax(a, axis=1) # 按行选取最大值的索引
        b3
        array([0, 0, 2], dtype=int64)

星号(*)的作用

列表前加星号作用是将列表解开成两个独立的参数，输入函数。
字典前加两个星号，是将字典解开成独立的元素作为形参。

ndarray.ndim代表的就是shape元组的长度。
numpy.linspace用法
numpy.linspace(start, shop, num==50, endpoint=True, retstep=False, dtype=None)
在指定间隔start到stop内返回均匀间隔的数组。
返回num均匀分布的样本，在[start, stop]，默认生成50个数据
endpoint， 如果是真，则一定包括stop，如果为False，一定不会有stop
retstep，是否显示步长信息

import numpy as np
y1 = np.linspace(-10.0,10.0) # 默认生成50个数据
y1
array([-10. , -9.59183673, -9.18367347, -8.7755102 ,
-8.36734694, -7.95918367, -7.55102041, -7.14285714,
-6.73469388, -6.32653061, -5.91836735, -5.51020408,
-5.10204082, -4.69387755, -4.28571429, -3.87755102,
-3.46938776, -3.06122449, -2.65306122, -2.24489796,
-1.83673469, -1.42857143, -1.02040816, -0.6122449 ,
-0.20408163, 0.20408163, 0.6122449 , 1.02040816,
1.42857143, 1.83673469, 2.24489796, 2.65306122,
3.06122449, 3.46938776, 3.87755102, 4.28571429,
4.69387755, 5.10204082, 5.51020408, 5.91836735,
6.32653061, 6.73469388, 7.14285714, 7.55102041,
7.95918367, 8.36734694, 8.7755102 , 9.18367347,
9.59183673, 10. ])

y2 = np.linspace(1,10,10) # 生成10个数据，包括首尾
y2
array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])

y3 = np.linspace(1,10,10,endpoint=False) # 不包括尾部数据
y3
array([1. , 1.9, 2.8, 3.7, 4.6, 5.5, 6.4, 7.3, 8.2, 9.1])

y4= np.linspace(1, 10, 6, retstep=True) # 将步长与结果的数组放入一个list、
y4
(array([ 1. , 2.8, 4.6, 6.4, 8.2, 10. ]), 1.8)

拉平操作 ravel()和faltten()及reshape(1,-1)的区别联系(补充[None,:]操作)

都是对numpy矩阵进行拉平处理，区别在于flatten()返回的仅仅是copy值，而ravel()返回的是实际的值，有点返回地址的意思。而x.reshape(1,-1)表示把向量 x reshape成一个行向量，注意的它仍然保持x的维度。
另外，Numpy中的 一维向量 有个特殊的用法，将行或者列设置成None，用来将矩阵转换成行或者列。偶尔会看到np.newaxis，这与None用法一致。
详见代码

import numpy as np
x = np.array([[1,2,3],[4,5,6],[1,2,3]])
x.flatten()
array([1, 2, 3, 4, 5, 6, 1, 2, 3]) # 拉平

x.ravel()
array([1, 2, 3, 4, 5, 6, 1, 2, 3])

x.ravel(‘F’)
array([1, 4, 1, 2, 5, 2, 3, 6, 3]) # 按列拉平

x.flatten(‘F’)
array([1, 4, 1, 2, 5, 2, 3, 6, 3])

x.flatten()[1] = 20
x
array([[1, 2, 3],
[4, 5, 6],
[1, 2, 3]])

x.ravel()[1] = 20
x
array([[ 1, 20, 3],
[ 4, 5, 6],
[ 1, 2, 3]])

x.reshape(1,-1) # 注意结果仍然是二维
array([[1, 2, 3, 4, 5, 6, 1, 2, 3]]) # 这里有两个方括号

x = np.array([1,2,3,6,7,8]) # 注意操作的是数组，即原x是数组
***>>> x[None,:] # 转成行向量(二维矩阵)
array([[1, 2, 3, 6, 7, 8]])

x[:,None] # 转成列向量(二维矩阵)***
array([[1],
[2],
[3],
[6],
[7],
[8]])

x[np.newaxis, :] # np.newaxis与None用法一致
array([[1, 2, 3, 6, 7, 8]])

np.prod() 计算元素乘积

默认计算矩阵所有元素的乘积，也可以通过axis计算指定轴的乘积

x = np.array([[1,2,3],[2,3,4]])
np.prod(x)
144

np.prod(x,axis=1)
array([ 6, 24])

np.prod(x,axis=0)
array([ 2, 6, 12])

把矩阵大于或小于N的元素置M的技巧

技巧包括 maximum() 函数 、minimum() 函数，以及 矩阵操作的技巧

import numpy as np
x = np.array([[1,2,3],[-3,2,4],[5,-2,9]])
x
array([[ 1, 2, 3],
[-3, 2, 4],
[ 5, -2, 9]])

y1 = np.maximum(0,x) # 把小于0的元素置0，比改变x的值
y1
array([[1, 2, 3],
[0, 2, 4],
[5, 0, 9]])

y2 = np.minimum(0,x) # 把大于0的元素置0，不改变x的值
y2
array([[ 0, 0, 0],
[-3, 0, 0],
[ 0, -2, 0]])

x1 = x.copy()
x1
array([[ 1, 2, 3],
[-3, 2, 4],
[ 5, -2, 9]])

x1[x1 < 0] = 0 # 把小于0的元素置0，改变x1的值
x1
array([[1, 2, 3],
[0, 2, 4],
[5, 0, 9]])

x2 = x.copy()
x2[x2 > 0] = 0 # 把大于0的元素置0，改变x2的值
x2
array([[ 0, 0, 0],
[-3, 0, 0],
[ 0, -2, 0]])

numpy中的矩阵copy问题

还记得Python的可变可不变对象不，简单温习一下：
不可变对象： 该对象所指向的内存中的值不能被改变。当改变某个变量的时候，由于其所指的值不能被改变，相当于把原来的值复制一份后再改变，这会开辟一个新的地址，变量再指向这个地址。
不可变对象包括 int string float tuple None
可变对象： 该对象所指向的内存中的值可以被改变。变量（准确说是引用）被改变后，实际上是其所指的值直接发生改变，并没有发生复制行为，也没有开辟新的地址，通俗点说就是原地改变。
可变对象包括 list dictionary set
numpy的narray用法就类似于可变对象，直接等于并不会开辟新的地址，改变赋值对象也就改变了原来的值。举例如下：

import numpy as np
x = np.array([[1,2,3],[-3,2,4],[5,-2,9]])
x
array([[ 1, 2, 3],
[-3, 2, 4],
[ 5, -2, 9]])

x1 = x.copy() # copy()，开辟新地址
x1[x1 > 0] = 0
x1
array([[ 0, 0, 0],
[-3, 0, 0],
[ 0, -2, 0]])

x # x不变
array([[ 1, 2, 3],
[-3, 2, 4],
[ 5, -2, 9]])

x2 = x # 直接等于，未开辟新地址，x2与x相关联
x2
array([[ 1, 2, 3],
[-3, 2, 4],
[ 5, -2, 9]])

x2[x2>0] = 0
x2
array([[ 0, 0, 0],
[-3, 0, 0],
[ 0, -2, 0]])

x # x也改变
array([[ 0, 0, 0],
[-3, 0, 0],
[ 0, -2, 0]])

x = np.array([[1,2,3],[-3,2,4],[5,-2,9]])
x3 = x[2] # 取x的第3行
x3
array([ 5, -2, 9])

x3[2] = 100 # 将x3第3个元素置100
x # x中对应的元素置也被置成100了
array([[ 1, 2, 3],
[ -3, 2, 4],
[ 5, -2, 100]])

np.zeros_like()构造全零矩阵，无需指定大小

复制矩阵的维度，但是元素全是0

import numpy as np
x = np.array([[1,2,3],[4,5,6]])
np.zeros_like(x) # 生成一个和x大小相同的全零矩阵
array([[0, 0, 0],
[0, 0, 0]])

random.rand和random.rand和random.randint区别

np.random.random() 生成一个随机数
产生 0 ~ 1 之间的随机浮点数，无输入参数

np.random.uniform()

产生随机浮点数

np.random.rand() 生成均匀分布矩阵
创建一个矩阵，服从[0,1]随机分布

import numpy as np
n = np.random.rand(3,4)

array([[0.11502462, 0.3503468 , 0.6206656 , 0.35172063],
[0.66367565, 0.10195004, 0.22708003, 0.9318615 ],
[0.77946053, 0.81804715, 0.2272248 , 0.17736476]])

np.random.randn() 生成正态分布矩阵

创建一个矩阵，服从N(0,1)标准正态分布。
一般正态分布N = ( μ , σ 2 ) N=(\mu ,\sigma^2)N=(μ,σ 2 )可通过 sigma * np.random.randn(…) + m 实现

import numpy as np
x = np.random.randn(2,3)

array([[-0.09382672, -0.97939614, 0.0222352 ],
[ 0.15060188, -0.01107968, 1.08374427]])

y = np.multiply(0.1,np.random.randn(2,3))+0.5 # 一般正太分布

array([[0.49305173, 0.36802044, 0.48699281],
[0.45197275, 0.53837051, 0.60022348]])

np.randm.randint() 生成离散均匀分布的整数值组成的矩阵

numpy.random.randint(low,high=None,size=None,dtype)
生成半开半闭区间[low, high)上离散均匀分布的整数值，未给出high时，区间变为[0, low)

import numpy as np
z = np.random.randint(2,9,(2,3))

array([[2, 3, 6],
[8, 2, 8]])

m = np.random.randint(9,size = (2,3))

array([[4, 0, 2],
[5, 2, 8]])

python 断言 assert

x = ‘You are right’
type(x)
<class ‘str’>

assert type(x)==str, ‘x is not str’
x = [1,2,3]
type(x)
<class ‘list’>

assert type(x)==str, ‘x is not str’
Traceback (most recent call last):
File “”, line 1, in
AssertionError: x is not str

乘法之间的区别

星号( * ) 和 .dot 和 np.multiply 的区别联系
A * B 表示 A 和 B 的对应元素相乘，其中 A 和 B 大小一致
np.multiply 与星号用法一致，均表示对应元素相乘
而 .dot 是矩阵运算中的点乘， A 的列数需要等于 B 的行数。

np.pad()函数进行padding操作

语法：

pad(array, pad_width, mode, **kwargs)返回值：数组

参数解释：

array——表示需要填充的数组；
pad_width——表示每个轴（axis）边缘需要填充的数值数目。
参数输入方式为：（(before_1, after_1), … (before_N, after_N)），其中(before_1, after_1)表示第1轴两边缘分别填充before_1个和after_1个数值。取值为：{sequence, array_like, int}
mode——表示填充的方式（取值：str字符串或用户提供的函数）,总共有11种填充模式；

填充方式：

‘constant’——表示连续填充相同的值，每个轴可以分别指定填充值，constant_values=（x, y）时前面用x填充，后面用y填充，缺省值填充0
‘edge’——表示用边缘值填充
‘linear_ramp’——表示用边缘递减的方式填充
‘maximum’——表示最大值填充
‘mean’——表示均值填充
‘median’——表示中位数填充
‘minimum’——表示最小值填充
‘reflect’——表示对称填充
‘symmetric’——表示对称填充
‘wrap’——表示用原数组后面的值填充前面，前面的值填充后面

#在数组A的边缘填充constant_values指定的数值
#（3,2）表示在A的第[0]轴填充（二维数组中，0轴表示行），即在0轴前面填充3个宽度的0，比如数组A中的95,96两个元素前面各填充了3个0；在后面填充2个0，比如数组A中的97,98两个元素后面各填充了2个0
#（2,3）表示在A的第[1]轴填充（二维数组中，1轴表示列），即在1轴前面填充2个宽度的0，后面填充3个宽度的0
np.pad(A,((3,2),(2,3)),‘constant’,constant_values = (0,0)) #constant_values表示填充值，且(before，after)的填充值等于（0,0）

代码示例：

import numpy as np        
A = np.arange(95,99).reshape(2,2)
A
array([[95, 96], [97, 98]])

np.pad(A,((3,2),(2,3)),‘constant’,constant_values = (0,0))
array([[ 0, 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0],
[ 0, 0, 95, 96, 0, 0, 0],
[ 0, 0, 97, 98, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0, 0]])
说明： 在矩阵行的上部分添加3行，下部分添加2行，在列的左部分添加2列，右部分添加3列。

b = np.array([[[1,2],[3,4]],[[3,4],[7,8]],[[4,5],[1,2]]])

b
array([[[1, 2],
[3, 4]],

[[3, 4],
[7, 8]],

[[4, 5],
[1, 2]]])

np.pad(b, ((0,0),(1,1),(1,1)), ‘constant’, constant_values = 0)
array([[[0, 0, 0, 0],
[0, 1, 2, 0],
[0, 3, 4, 0],
[0, 0, 0, 0]],

[[0, 0, 0, 0],
[0, 3, 4, 0],
[0, 7, 8, 0],
[0, 0, 0, 0]],

[[0, 0, 0, 0],
[0, 4, 5, 0],
[0, 1, 2, 0],
[0, 0, 0, 0]]])

numpy.empty() 创建指定形状和数据类型且未初始化的数组

numpy.empty 方法用来创建一个指定形状（shape）、数据类型（dtype）且未初始化的数组

numpy.empty(shape, dtype = float, order = ‘C’)
1
shape数组形状
dtype数据类型，可选
order有"C"和"F"两个选项,分别代表，行优先和列优先，在计算机内存中的存储元素的顺序。

import numpy as np
x = np.empty([3,2], dtype = int)
print (x)

输出：

[[ 6917529027641081856 5764616291768666155]
[ 6917529027641081859 -5764598754299804209]
[ 4497473538 844429428932120]]

数组元素为随机值，因为它们未初始化。
判断两个矩阵元素完全相等&&存在相等

(ab).all() 判断是否完全相等
(ab).any() 判断是否存在元素相等

a = np.array([[1,2,3][1,2,3]])
b = np.array([[1,2,3][1,2,3]])
c = np.array([[1,4,3][1,2,3]])
print((ab).all()) # 是否完全相等 True
print((ac).all()) # False
print((a==c).any()) # 是否存在元素相等 True

关于 np.mat() 的使用

np.array() 更具有通用性，np.mat 只适用于二维矩阵
np.mat() 和 np.matrix() 都可以将 list 转换为 numpy.matrix 类型的矩阵，而 np.array() 不行
np.full 用于形成元素全为某元素的矩阵

np.full(shape, val): 生成形为 shape 的元素全为 val 的矩阵

astype 转换数据类型

import numpy as np
c = np.array([[1,2],[3,4]])
c
array([[1, 2],
[3, 4]])

c.astype(np.float32)
array([[1., 2.],
[3., 4.]], dtype=float32)

np.meshgrid() 快速生成网格

meshgrid(x,y) 可用于快速生成由于 x轴坐标 x 和 y 轴坐标 y 组合的网格点

import numpy as np
x = np.array([1,3,5])
y = np.array([4,6])
XX,YY = np.meshgrid(x,y)
XX
array([[1, 3, 5],
[1, 3, 5]])

YY
array([[4, 4, 4],
[6, 6, 6]])

这样就组合成 (1,4) (3,4) (5,4) (1,6) (3,6) (5.6) 的网格点

np.hstack() 和 np.vstack() 用于堆叠矩阵

注意下面的 M 是 tuple 形式，如 (x,y)，x和y均为 np.array 形式的矩阵
np.vstack(M) 用于沿着竖直方向将矩阵堆叠起来
np.hstack(M) 用于沿着水平方向将矩阵堆叠起来

import numpy as np
x = np.array([[3,4,5],[1,3,4]])
y = np.array([[1,1,1],[2,2,2]])
np.hstack((x,y)) # 水平堆叠
array([[3, 4, 5, 1, 1, 1],
[1, 3, 4, 2, 2, 2]])

np.vstack((x,y)) # 竖直堆叠
array([[3, 4, 5],
[1, 3, 4],
[1, 1, 1],
[2, 2, 2]])

numpy 取整

np.round 和 np.around 一致，均是四舍五入运算，默认取整，可通过 decimals 调整小数位数
np.floor 是向下取整操作
np.ceil 是向上取整操作

import numpy as np
a = np.array([0.125,0.568,5.688])
np.round(a) # 四舍五入取整， np.around 和 round 用法一致
array([0., 1., 6.])

np.round(a,decimals = 2) # 四舍五入保留2位小数
array([0.12, 0.57, 5.69])

np.floor(a) # 向下取整
array([0., 0., 5.])

np.ceil(a) # 向上取整
array([1., 1., 6.])

np.newaxis 在特定位置增加一个维度

记着 c[:,np.newaxis] 是将矩阵c再加一个维度，如果c是一维的，那么这个表达式是将 c 变成列向量， c[np.newaxis,:] 是将矩阵 c 变成行向量。
看例子

import numpy as np
c = np.array([1,2,5,4])
c[:,np.newaxis]
array([[1],
       [2],
       [5],
       [4]])
c[np.newaxis,:]
array([[1, 2, 5, 4]])

python 广播机制

Numpy要求输入的数组shape一致，当shape不一致的时候，则会使用广播机制，调整数组的shape一致，否则出错。
广播的原则：如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为1，则认为它们是广播兼容的。广播会在缺失和（或）长度为1的维度上进行。

这句话乃是理解广播的核心。广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为1。

广播机制的四条规则如下：

1、让所有输入数组都向其中shape最长的数组看齐，shape中不足的部分都通过在前面加1补齐

2、输出数组的shape是输入数组shape的各个轴上的最大值

3、如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为1时，这个数组能够用来计算，否则出错

4、当输入数组的某个轴的长度为1时，沿着此轴运算时都用此轴上的第一组值

import numpy as np
a = np.array([[1,2,3],[4,5,6]])
a = np.array([[1,2,3,6],[4,5,6,6]])
a1 = a.reshape((1,2,4))
a1
array([[[1, 2, 3, 6],
[4, 5, 6, 6]]])

b = np.array([[3,4,5,6],[1,2,3,4],[4,5,5,5]])
b
array([[3, 4, 5, 6],
[1, 2, 3, 4],
[4, 5, 5, 5]])

b1 = b.reshape((1,3,4)).transpose((1,0,2))
b1
array([[[3, 4, 5, 6]],

 [[1, 2, 3, 4]],

 [[4, 5, 5, 5]]])

a1
array([[[1, 2, 3, 6],
[4, 5, 6, 6]]])

a1+b1
array([[[ 4, 6, 8, 12],
[ 7, 9, 11, 12]],

 [[ 2,  4,  6, 10],
  [ 5,  7,  9, 10]],

  [[ 5,  7,  8, 11],
  [ 8, 10, 11, 11]]])

上面这个例子中，a1 是 [1,2,4] 维度的数组，b1 是 [3,1,4] 维度的数组，可以如此理解，他们相加后由于广播机制的作用应该生成 [3,2,4] 大小的数组。那么我们将 a1 扩展成 [3,2,4] 成

[[[1, 2, 3, 6],
[4, 5, 6, 6]],
[[1, 2, 3, 6],
[4, 5, 6, 6]],
[[1, 2,3, 6],
[4, 5, 6, 6]]]

将 b1 扩展成 [3,2,4] 成

[[[3, 4, 5, 6],
[3, 4, 5, 6]],
[[1, 2, 3, 4],
[1, 2, 3, 4]],
[[4, 5,5, 5],
[4, 5, 5, 5]]]

扩展后的 a1 和 b1 相加得到

[[ 4, 6, 8, 12],
[ 7, 9, 11, 12]],
[[ 2, 4, 6, 10],
[ 5, 7, 9, 10]],
[[ 5, 7, 8, 11],
[ 8, 10, 11, 11]]]

即为通过广播机制相加的结果。

详见 Numpy中的广播操作 https://blog.csdn.net/qq_36387683/article/details/80628577
用一幅图说明其广播机制：

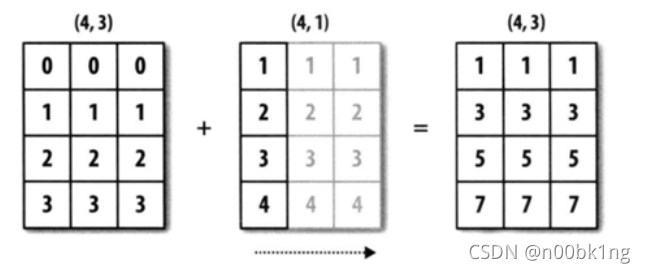
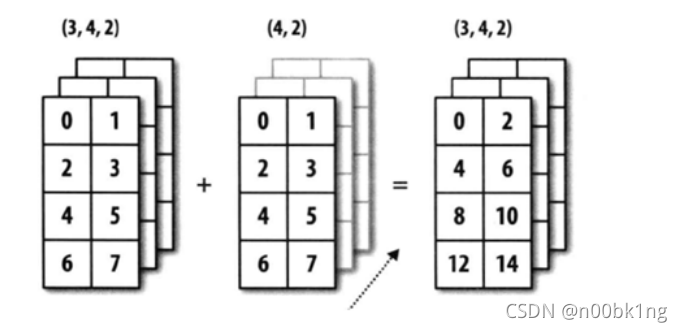
numpy.transpose()转置

transpose()是以交换维度的方式进行转置。如

c = np.array([[[1,2,5],[3,4,6]],[[4,5,6],[7,8,9]]])
c
array([[[1, 2, 5],
[3, 4, 6]],

[[4, 5, 6],
[7, 8, 9]]])

c.transpose(1,0,2) # 将c的维度按照 第1维度，第0维度，第2维度的排序排成 第0,1,2维度
array([[[1, 2, 5],
[4, 5, 6]],

   [[3, 4, 6],
   [7, 8, 9]]])

如原来的 4 （4,5,6的4）本是 (1,0,0), 转换后变为 (0,1,0)

c.transpose(1,2,0) # 将c的维度按照 第1维度，第2维度，第0维度的排序排成 第0,1,2维度
array([[[1, 4],
[2, 5],
[5, 6]],

   [[3, 7],
   [4, 8],
   [6, 9]]])

如原来的 4 （4,5,6的4）本是 (1,0,0), 转换后变为 (0,0,1)

常用来对 numpy 图片矩阵作转换

在opencv中，图片格式为 H W C，即长宽和维度，而一般图像处理的时候习惯用 C H W，故可以用 transpose 对维度进行变换
img = cv2.imread(“111.jpg”)
img_ = img[:,:,::-1] # cv2 读取的是 BGR，::-1 将C通道按照RGB取反
img_convet = img_.transpose((2,0,1)) # 将 H W C 转为 C H W

numpy 中双冒号的用法

numpy 中 ndarray 对象内容可以索引或切片来访问和修改。可以通过 start:stop:step 来进行切片操作，如下

import numpy as np
a = np.array([2,2,3,4,5,5,6,7])
a[0:7:2]
array([2, 3, 5, 6])

而双冒号实则是两个冒号之间缺省了必要的值，它省略的是 stop 值，那么 stop 值就默认尾部。如下

import numpy as np
a = np.array([2,2,3,4,5,5,6,7])
a[0::2]
array([2, 3, 5, 6])

除了一般的切片用法，也常用 [::-1] 来将序列按倒序排列。

a[::-1]
array([7, 6, 5, 5, 4, 3, 2, 2])

一般而言，python 的内置函数 slice 就实现了此功能，用法是 slice(start, stop, step)。如

import numpy as np
a = np.array([2,2,3,4,5,5,6,7])
s = slice(0,7,2)
a[s]
array([2, 3, 5, 6])

引用链接：https://blog.csdn.net/phyiscslogical/article/details/119982566
https://blog.csdn.net/weixin_39704651/article/details/100573665
https://blog.csdn.net/weixin_38736140/article/details/79804255
https://blog.csdn.net/qq_37692302/article/details/106099667