学习心得
第一章:基础知识
零、学习总结
(1)scikit-learn 依赖于另外两个 Python 包:NumPy 和 SciPy。若想绘图和进行交互式开发,还应该安装 matplotlib、IPython 和 Jupyter Notebook。
(2)如果不熟悉 NumPy 或 matplotlib,推荐阅读 SciPy 讲稿(http://www.scipy-lectures.org/)的第1章
(3)《python机器学习基础》代码:https://github.com/amueller/introduction_to_ml_with_python,其中mglearn是本书编写的实用函数库。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn
本系列原书代码的包版本如下,不一定要相同,但是sklearn不能低于0.18(0.18增加了model_selection模块)。
Python version: 3.5.2 |Anaconda 4.1.1 (64-bit)| (default, Jul 2 2016, 17:53:06)
[GCC 4.4.7 20120313 (Red Hat 4.4.7-1)]
pandas version: 0.18.1
matplotlib version: 1.5.1
NumPy version: 1.11.1
SciPy version: 0.17.1
IPython version: 5.1.0
scikit-learn version: 0.18
(4)如果不使用魔法命令,如果你没有使用 Jupyter Notebook 或
魔法命令%matplotlib notebook或%matplotlib inline 来显示图像,那么就需要调用 plt.show 来显示图像.
scikit-learn 中的约定:数组中包含 150 朵不同的花的测量数据。前面说过,机器学习中的个体叫作样本(sample),其属性叫作特征(feature)。data 数组的形状(shape)是样本数乘以特征数。
一、基础工具包使用
(1)pandas使用
可以参考之前的总结(【小白学数据分析】task1-数据基础操作和pandas)。
- 一个pandas DataFrame是一张类似excel的表格(有大量修改和操作表格的方法,尤其可以像SQL一样对表格进行查询和连接)
- Numpy要求数组中所有元素类型相同,而pandas每一列的数据类型可以互不相同
- pandas可以从SQL、Excel文件和逗号分隔值(CSV)文件。
如现在如下创建关于人的简单数据集,利用字典创建DataFrame:
import pandas as pd
# create a simple dataset of people
data = {'Name': ["John", "Anna", "Peter", "Linda"],
'Location' : ["New York", "Paris", "Berlin", "London"],
'Age' : [24, 13, 53, 33]
}
data_pandas = pd.DataFrame(data)
# IPython.display allows "pretty printing" of dataframes
# in the Jupyter notebook
display(data_pandas)

(2)SciPy使用
SciPy 中最重要的是 scipy.sparse(稀疏矩阵):
from scipy import sparse
# 创建一个二维对角单位矩阵
eye = np.eye(4)
print("NumPy array:\n", eye)
# NumPy array:
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
CSR格式的稀疏矩阵:
# Convert the NumPy array to a SciPy sparse matrix in CSR format
# 将Numpy数组转换成CSR格式的稀疏矩阵
# Only the nonzero entries are stored
# 只保存非零元素
sparse_matrix = sparse.csr_matrix(eye)
print("\nSciPy sparse CSR matrix:\n", sparse_matrix)
# SciPy sparse CSR matrix:
(0, 0) 1.0
(1, 1) 1.0
(2, 2) 1.0
(3, 3) 1.0
COO格式的稀疏矩阵:
data = np.ones(4)
row_indices = np.arange(4)
col_indices = np.arange(4)
eye_coo = sparse.coo_matrix((data, (row_indices, col_indices)))
print("COO representation:\n", eye_coo)
# COO representation:
(0, 0) 1.0
(1, 1) 1.0
(2, 2) 1.0
(3, 3) 1.0
(3)matplotlib
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# Generate a sequence of numbers from -10 to 10 with 100 steps in between
x = np.linspace(-10, 10, 100)
# Create a second array using sine
y = np.sin(x)
# The plot function makes a line chart of one array against another
plt.plot(x, y, marker="x")

二、小栗子应用
1.初识数据
2.划分训练&测试数据
3.观察数据
4.构建KNN模型预测鸢尾花
fit、predict 和score 方法是 scikit-learn 监督学习模型中最常用的接口。
(1)k 近邻分类算法,根据新数据点在训练集中距离最近的邻居来进行预测。该算法在KNeighborsClassifier 类中实现,里面既包含构建模型的算法,也包含利用模型进行预测的算法。我们将类实例化,并设定参数。
(2)然后调用 fit 方法来构建模型,传入训练数据(X_train)和训练输出(y_trian)作为参数。
(3)我们用 score 方法来评估模型,该方法计算的是模型精度。
我们将 score 方法用于测试集数据和测试集标签,得出模型的精度约为 97%,也就是说,该模型在测试集上 97% 的预测都是正确的.
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
knn = KNeighborsClassifier(n_neighbors=1)
X_train, X_test, y_train, y_test = train_test_split(
iris_dataset['data'], iris_dataset['target'], random_state=0)
knn = KNeighborsClassifier(n_neighbors=1)
# 要将该类实例为一个对象,才能用这个模型
knn.fit(X_train, y_train)
# 基于训练集来构建模型,调用knn对象的fit方法
print("Test set score: {:.2f}".format(knn.score(X_test, y_test)))
# 输出Test set score: 0.97
所以知道模型在测试集的精度约为0.97。
我们要对测试数据中的每朵鸢尾花进行预测,并将预测结果与标签(已知的品种)进行对比。
上面我们是通过使用knn对象的score方法来计算测试集的精度;我们也可以通过计算精度(品种预测正确的花所占的比例)衡量模型优劣:
print("Test set score: {:.2f}".format(np.mean(y_pred == y_test)))
# 打印Test set score: 0.97
如果要预测一朵鸢尾花(花萼长 5cm 宽2.9cm,花瓣长 1cm 宽0.2cm)属于啥品种,可将该数据放在一个Numpy数组(数组形状为样本数1乘以特征数4),注意sklearn的输入数据必须是二维数组(所以要再转换为二维Numpy数组的一行):
X_new = np.array([[5, 2.9, 1, 0.2]])
print("X_new.shape: {}".format(X_new.shape))
# 打印X_new.shape: (1, 4)
prediction = knn.predict(X_new)
print("Prediction: {}".format(prediction))
print("Predicted target name: {}".format(
iris_dataset['target_names'][prediction]))
结果如下,即通过knn对象的predict方法预测出该花属于类别0(setosa品种),根据上面的精度97%,所以我们有97%的把握预测是对的。
Prediction: [0]
Predicted target name: ['setosa']
第二章:监督学习
零、学习总结
(1)sklearn中的数据集通常被保存为Bunch对象(和字典类似,Bunch可用点操作符来访问对象的值(比如用bunch.key来代替bunch['key']))。更多的模型的参数和选项可以参考sklearn官方文档(http://scikit-learn.org/stable/documentation)
(2)以下常用的监督学习算法总结(使用场景):
- 最近邻:适用于小型数据集,是很好的基准模型,很容易解释。
- 线性模型:非常可靠的首选算法,适用于非常大的数据集,也适用于高维数据。
- 朴素贝叶斯:只适用于分类问题。比线性模型速度还快,适用于非常大的数据集和高维数据。精度通常要低于线性模型。
- 决策树:速度很快,不需要数据缩放,可以可视化,很容易解释。
- 随机森林:几乎总是比单棵决策树的表现要好,鲁棒性很好,非常强大。不需要数据缩放。不适用于高维稀疏数据。
- 梯度提升决策树:精度通常比随机森林略高。与随机森林相比,训练速度更慢,但预测速度更快,需要的内存也更少。比随机森林需要更多的参数调节。
- 支持向量机:对于特征含义相似的中等大小的数据集很强大。需要数据缩放,对参数敏感。
- 神经网络:可以构建非常复杂的模型,特别是对于大型数据集而言。对数据缩放敏感,对参数选取敏感。大型网络需要很长的训练时间。
一、前置知识
(1)分类与回归
分类问题的目标是预测类别标签;
回归问题的目标是预测一个连续值(浮点数);
区分分类和回顾的方法:输出是否具有某种连续性。


(2)泛化、过拟合、欠拟合
泛化:训练数据上构建的模型能够对新数据做出准确预测,就说能从训练集泛化(generalize)到测试集。

过拟合:训练集表现好,但不能泛化到新数据上的模型即存在过拟合。
欠拟合:无法抓住数据的全部内容以及数据中的变化,模型甚至在训练集上的表现很差。
PS:收集更多的数据,适当构建更复杂的模型,对监督学习往往特别有用,甚至比模型调参更有效。
二、监督学习算法
2.0 了解几个样本数据集
(1)从特征较少的数据集(也叫低维数据集)中得出的结论可能并不适用于特征较多的数据集(也叫高维数据集)。
(2)包含在sklearn中的数据集通常被保存为Bunch对象(类似字典),可以用bunch.key代替bunch['key']。如下加载sklearn自带的癌症数据集(benign良性,malignant恶性)。
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print("cancer.keys():\n", cancer.keys())
# cancer.keys():
# dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])
print("Shape of cancer data:", cancer.data.shape)
# Shape of cancer data: (569, 30)
print("Sample counts per class:\n",
{n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))})
# Sample counts per class:
# {'malignant': 212, 'benign': 357}
print("Feature names:\n", cancer.feature_names)
"""
Feature names:
['mean radius' 'mean texture' 'mean perimeter' 'mean area'
'mean smoothness' 'mean compactness' 'mean concavity'
'mean concave points' 'mean symmetry' 'mean fractal dimension'
'radius error' 'texture error' 'perimeter error' 'area error'
'smoothness error' 'compactness error' 'concavity error'
'concave points error' 'symmetry error' 'fractal dimension error'
'worst radius' 'worst texture' 'worst perimeter' 'worst area'
'worst smoothness' 'worst compactness' 'worst concavity'
'worst concave points' 'worst symmetry' 'worst fractal dimension']
"""
(3)需要扩展这个数据集,输入特征不仅包括这 13 个测量结果,还包括这些特征之间的乘积(也叫交互项)。我们不仅将犯罪率和公路可达性作为特征,还将犯罪率和公路可达性的乘积作为特征。像这样包含导出特征的方法叫作特征工程。
2.1 KNN
模型训练。
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)
clf.fit(X_train, y_train)
print("Test set predictions:", clf.predict(X_test))
# 打印Test set predictions: [1 0 1 0 1 0 0]
print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test)))
# 打印Test set accuracy: 0.86
其中上面的mglearn的make_forge数据集函数具体如下:
def make_forge():
# a carefully hand-designed dataset lol
X, y = make_blobs(centers=2, random_state=4, n_samples=30)
y[np.array([7, 27])] = 0
mask = np.ones(len(X), dtype=np.bool)
mask[np.array([0, 1, 5, 26])] = 0
X, y = X[mask], y[mask]
return X, y
分析KNN模型训练,在xy平面上画出所有测试点的预测结果,根据平面中所属的类别对平面进行着色,并且查看决策边界。如下图即对1个、3个、9个邻居三种情况的决策边界可视化——邻居个数越多,决策边界越平滑。更平滑的边界对应更简单的模型。
假如考虑极端情况,即邻居个数等于训练集中所有数据点的个数,
那么每个测试点的邻居都完全相同(即所有训练点),所有预测结果也完全相同(即训练
集中出现次数最多的类别)。

仅考虑单一近邻时,训练集上的预测结果十分完美。但随着邻居个数的增多,模型变得更简单,训练集精度也随之下降。
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=66)
training_accuracy = []
test_accuracy = []
# try n_neighbors from 1 to 10
neighbors_settings = range(1, 11)
for n_neighbors in neighbors_settings:
# build the model
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
clf.fit(X_train, y_train)
# record training set accuracy
training_accuracy.append(clf.score(X_train, y_train))
# record generalization accuracy
test_accuracy.append(clf.score(X_test, y_test))
plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend()

小结:KNN有2个重要参数:邻居个数、数据点之前距离的度量方法;如果训练集很大(特征数很多或者样本数很大),预测速度可能会很慢,对于稀疏数据集(大多数特征的大多数取值为0的数据集)的算法效果也不好。
2.2 线性模型
线性模型有很多种算法。这些算法的区别在于以下两点:
? 系数和截距的特定组合对训练数据拟合好坏的度量方法;
? 是否使用正则化,以及使用哪种正则化方法。
1.用于回归的线性模型
对于有多个特征的数据集而言,线性模型可以非常强大。特别地,如果特征数量大于训练数据点的数量,任何目标 y 都可以(在训练集上)用线性函数完美拟合。
2.线性回归(最小二乘法)
对于更高维的数据集(即有大量特征的数据集),线性模型将变得更加强大,过拟合的可能性也会变大。
3.正则化regularization
(1)Lasso回归:加入L惩罚项(|a|+|b|+|c|)即参数(a,b,c)的L1-norm(L1范数)
(2)ridge回归(即岭回归):加入惩罚项(a^2 + b^2 +c^2)即参数(a,b,c)的L2-norm(L2范数)。ridge约束更强(所以不容易过拟合)。直观上看,系数尽量小(即每个特征对输出的影响应尽可能小)
小结:
(1)复杂度更小的模型意味着在训练集上的性能更差,但泛化性能更好。由于我们只对泛化性能感兴趣,所以应该选择 Ridge 模型而不是 LinearRegression 模型。
(2)简单性和训练集性能二者对于模型的重要程度可以由用户通过设置 alpha 参数(默认alpha=1.0)来指定。增大 alpha 会使得系数更加趋向于 0,从而降低训练集性能,但可能会提高泛化性能。
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test, y_test)))
# Training set score: 0.89
# Test set score: 0.75
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge10.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge10.score(X_test, y_test)))
#Training set score: 0.79
#Test set score: 0.64
ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge01.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge01.score(X_test, y_test)))
# Training set score: 0.93
# Test set score: 0.77
更大的 alpha 表示约束更强的模型,所以我们预计大 alpha 对应的 coef_元素比小 alpha 对应的 coef_ 元素要小。这一点可以在下图中得到证实:
plt.plot(ridge.coef_, 's', label="Ridge alpha=1")
plt.plot(ridge10.coef_, '^', label="Ridge alpha=10")
plt.plot(ridge01.coef_, 'v', label="Ridge alpha=0.1")
plt.plot(lr.coef_, 'o', label="LinearRegression")
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
xlims = plt.xlim()
plt.hlines(0, xlims[0], xlims[1])
plt.xlim(xlims)
plt.ylim(-25, 25)
plt.legend()
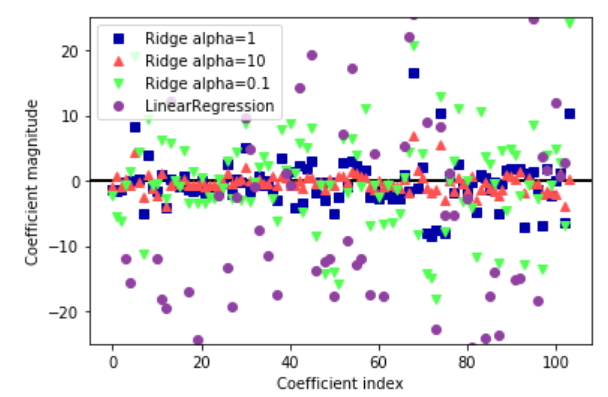
与 Ridge 类似,Lasso 也有一个正则化参数 alpha,可以控制系数趋向于 0 的强度。在上一个例子中,我们用的是默认值 alpha=1.0。为了降低欠拟合,我们尝试减小 alpha。这么做的同时,我们还需要增加 max_iter 的值(运行迭代的最大次数)。
4.用于分类的线性模型
y ^ = w [ 0 ] ? x [ 0 ] + w [ 1 ] ? x [ 1 ] + ? + w [ p ] ? x [ p ] + b > 0 \hat{y}=w[0] * x[0]+w[1] * x[1]+\cdots+w[p] * x[p]+b>0 y^?=w[0]?x[0]+w[1]?x[1]+?+w[p]?x[p]+b>0 对于用于分类的线性模型,决策边界是输入的线性函数。换句话说,(二元)线性分类器是利用直线、平面或超平面来分开两个类别的分类器。
(1)最常见的两种线性分类算法是 Logistic 回归(PS:logistic regression,不是回归算法,是分类算法)和线性支持向量机(linear support vector machine,线性 SVM),前者在linear_model.LogisticRegression 中实现,
后者在 svm.LinearSVC(SVC 代表支持向量分类器)中实现。
(2)对于 LogisticRegression 和 LinearSVC,决定正则化强度的权衡参数叫作 C。C 值越大,对应的正则化越弱。换句话说,如果参数 C 值较大,那么 LogisticRegression 和 LinearSVC 将尽可能将训练集拟合到最好,而如果 C 值较小,那么模型更强调使系数向量(w)接近于 0。
较小的 C 值可以让算法尽量适应“大多数”数据点,而较大的 C 值更强调每个数据点都分类正确的重要性。
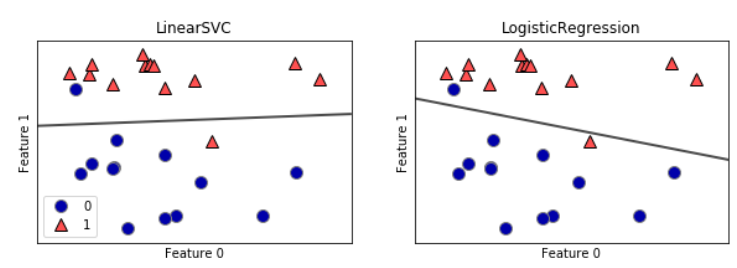
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
X, y = mglearn.datasets.make_forge()
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
clf = model.fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5,
ax=ax, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_title(clf.__class__.__name__)
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
axes[0].legend()
其中上面的mglearn的make_forge数据集函数具体如下:
def make_forge():
# a carefully hand-designed dataset lol
X, y = make_blobs(centers=2, random_state=4, n_samples=30)
y[np.array([7, 27])] = 0
mask = np.ones(len(X), dtype=np.bool)
mask[np.array([0, 1, 5, 26])] = 0
X, y = X[mask], y[mask]
return X, y
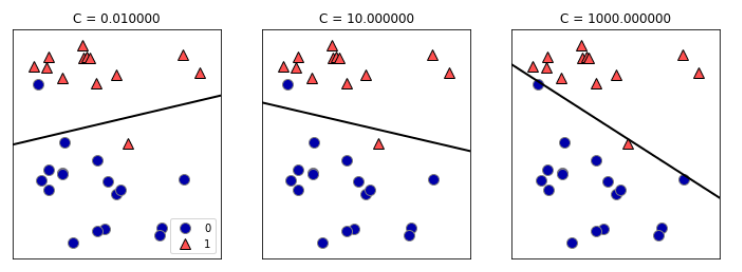
mglearn.plots.plot_linear_svc_regularization()
在中间的图(下图)中,C 值稍大,模型更关注两个分类错误的样本,使决策边界的斜率变大。右侧图中的模型尽量使所有点的分类都正确,但可能无法掌握类别的整体分布。换句话说,这个模型很可能过拟合。
5.用于多分类的线性模型
许多线性分类模型只适用于二分类问题,不能轻易推广到多分类问题(除了逻辑回归)。
所以将二分类推广到多分类算法的方法一般有:
(1)一对其余(one-vs rest):每个类别都学习一个二分类模型,将这个类别与其它类别尽量分开——最后生成与类别个数一样多的二分类模型,而在测试点上运行所有这些二分类模型来进行预测(在对应类别上分数最高的分类器则“胜出”,将这个类别标签返回作为预测结果)。
%matplotlib inline
# 第一种方法应用在一个简单的三分类数据集上
# 每个类别的数据都是从一个高斯分布中采样得出的
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import mglearn
X, y = make_blobs(random_state=42)
# 用mglearn的函数用于分类可视化
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
# X,前者对应特征1,后者对应特征2
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(["Class 0", "Class 1", "Class 2"])
# 在上面的训练集上训练一个 LinearSVC 分类器
linear_svm = LinearSVC().fit(X, y)
print("Coefficient shape: ", linear_svm.coef_.shape)
print("Intercept shape: ", linear_svm.intercept_.shape)
# 打印出 Coefficient shape: (3, 2)
# 打印出 Intercept shape: (3,)
上面代码的打印结果中,coef_ 的形状是 (3, 2),说明 coef_ 每行包含三个类别之一的系数向量,每列包含某个特征(这个数据集有 2 个特征)对应的系数值。现在 intercept_ 是一维数组,保存每个类别的截距。

将这 3 个二类分类器给出的直线可视化:
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
'Line class 2'], loc=(1.01, 0.3))

但图像中间的三角形区域属于哪一个类别呢,3 个二类分类器都将这一区域内的点划为
“其余”。——答案是分类方程结果最大的那个类别,即最接近的那条线对应的类别。
(2)多分类逻辑回归:与(1)稍不相同,但也是对每个类别都有一个系数向量和一个截距,也使用了相同的预测方法。
tips:方法链
如下方法的调用的拼接(先调用__init__,然后调用fit)成为方法链。
# 用一行代码初始化模型并拟合
logreg = LogisticRegression().fit(X_train, y_train)
# 法二:
logreg = LogisticRegression()
y_pred = logreg.fit(X_train, y_train).predict(X_test)
当然也可以在一行代码内完成模型的初始化、拟合和预测过程,但是这样可读性不强,拟合后的回归模型也没有保存在任何变量中(我们即不能查看也不能用来预测其他数据):
# 法三:
y_pred = LogisticRegression().fit(X_train, y_train).predict(X_test)
6.线性模型小结
(1)线性模型的主要参数是正则化参数,在回归模型中叫作 alpha,在 LinearSVC 和 LogisticRegression 中叫作 C。alpha 值较大或 C 值较小,说明模型比较简单。
(2)假定只有几个特征是真正重要的,那么你应该用L1 正则化,否则应默认使用 L2 正则化。如果模型的可解释性很重要的话,使用 L1 也会有帮助。
(3)线性模型可以推广到非常大的数据集,对
稀疏数据也很有效(训练速度和预测速度快)。利用我们之间见过的用于回归和分类的公式,理解如何进行预测是相对比较容易的。
(4)特征数大于样本数,线性模型的表现通常很好。
2.3 朴素贝叶斯分类器
BernoulliNB 分类器计算每个类别中每个特征不为 0 的元素个数。
小栗子:有 4 个数据点,每个点有 4 个二分类特征。一共有两个类别:0 和 1。对于类别 0(第 1、3 个数据点),第一个特征有 2 个为零、0 个不为零,第二个特征有 1 个为零、1 个不为零,以此类推。然后对类别 1 中的数据点计算相同的计数。计算每个类别中的非零元素个数:
X = np.array([[0, 1, 0, 1],
[1, 0, 1, 1],
[0, 0, 0, 1],
[1, 0, 1, 0]])
y = np.array([0, 1, 0, 1])
counts = {}
for label in np.unique(y):
# 对每个类别label进行遍历
# 计算(求和)每个特征中1的个数
counts[label] = X[y == label].sum(axis=0)
print("Feature counts:\n", counts)
# Feature counts:
# {0: array([0, 1, 0, 2]), 1: array([2, 0, 2, 1])}
小结:
(1) alpha 的工作原理:算法向数据中添加 alpha 这么多的虚拟数据点,这些点对所有特征都取正值。这可以将统计数据“平滑化”(smoothing)。alpha 越大,平滑化越强,模型复杂度就越低。
(2)朴素贝叶斯模型的许多优点和缺点都与线性模型相同。它的训练和预测速度都很快,训练过程也很容易理解。该模型对高维稀疏数据的效果很好,对参数的鲁棒性也相对较好。朴素贝叶斯模型是很好的基准模型,常用于非常大的数据集,在这些数据集上即使训练线性模型可能也要花费大量时间。
| GaussianNB | MultinomialNB | BernoulliNB | |
|---|---|---|---|
| 适用数据 | 高维数据 | 稀疏计数数据 | 稀疏计数数据(比如文本等) |
| 计算额统计数据类型 | 保存每个类别中每个特征的平均值和标准差。 | 计算每个类别中每个特征的平均值 | 计算每个类别中每个特征不为 0 的元素个数 |
| 预测公式 | —— | 和线性模型相同 | 和线性模型相同 |
2.4 决策树
注意:下载graphviz后,需要将dot(dot格式是一种用于保存图形的文本文件格式)加入到环境变量中,否则会报报错:https://blog.csdn.net/NT0521/article/details/89742824,另外加入环境变量后好像要重启才可以。
防止过拟合的两种策略:预剪枝和后剪枝。
(1)预剪枝的限制条件可能包括限制树的最大深度、限制叶结点的最大数目,或者规定一个结点中数据点的最小数目来防止继续划分。
(2)scikit-learn 的决策树在 DecisionTreeRegressor 类和 DecisionTreeClassifier 类中实现。scikit-learn 只实现了预剪枝,没有实现后剪枝。
%matplotlib inline
import mglearn
import matplotlib.pyplot as plt
mglearn.plots.plot_tree_progressive()

没错。。生成的下图右图就是有点模糊。下图左图有点过拟合了——,可以看到该图右方,这个决策边界(蓝色竖线)过于关注远离同类别其他点的单个异常点,即有一小条属于类别0的区域,包围着最右侧属于类别0的那个点。

2.5 决策树集成
2.6 核支持向量机
2.7 深度学习
三、分类器的不确定度估计
3.1 决策函数
3.2 预测概率
3.3 多分类问题的不确定度
Reference
(1)sklearn中文文档:https://scikitlearn.com.cn/
(2)