2 队列

队列是一种先进先出的数据结构
First in First out

2.1 数组队列的实现

Queue

void enqueue(E)，队尾添加数据，复杂度O(1)
E dequeue()，队首去除数据，复杂度O(n)
boolean isEmpty()
int getSize()

2.2 定义队列接口

public interface Queue<E> {
    int getSize();
    boolean isEmpty();
    void enqueue(E e);
    E dequeue();
    E getFront();
}

2.3 实现队列接口

public class ArrayQueue<E> implements Queue<E> {
    private Array<E> array;

    public ArrayQueue(int capacity) {
        array = new Array<>(capacity);
    }

    public ArrayQueue() {
        array = new Array<>();
    }

    @Override
    public int getSize() {
        return array.getSize();
    }

    public int getCapacity() {
        return array.getCapacity();
    }

    @Override
    public boolean isEmpty() {
        return array.isEmpty();
    }

    @Override
    public void enqueue(E e) {
        array.addLast(e);
    }

    @Override
    public E dequeue() {
        return array.removeFirst();
    }

    @Override
    public E getFront() {
        return array.getFirst();
    }

    @Override
    public String toString() {
        return "ArrayQueue{" +
                "array=" + array +
                '}';
    }
}

2.4 测试队列

public class Main {
    public static void main(String[] args) {
        ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
        for(int i=0; i<10; i++) {
            arrayQueue.enqueue(i);
            System.out.println(arrayQueue);

            if(i%3 == 2) {
                arrayQueue.dequeue();
                System.out.println(arrayQueue);
            }
        }
    }
}

2.5 循环队列

为了降低数组队列移除队首数据时的复杂度，有人提出了循环队列。

队列为空

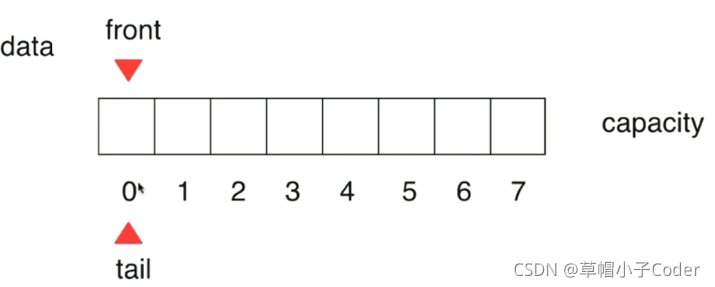
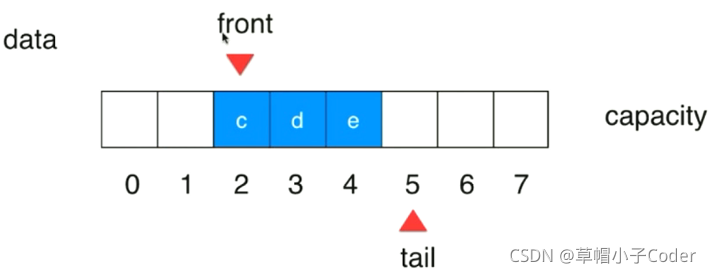
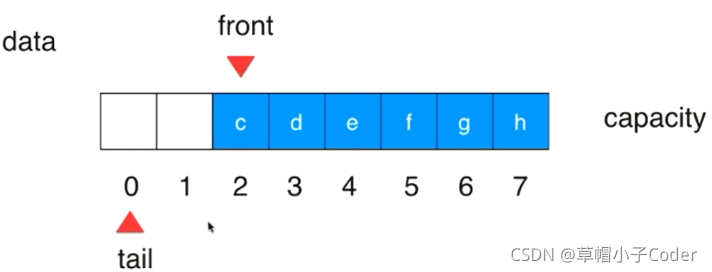
在这里插入图片描述

当循环队列为空时，队首指针front和队尾指针tail指向同一个位置，当循环队列不为空时，队首指针和队尾指针不再指向同一个位置。在队首移出数据或者队尾添加数据时，front和tail均会分别进行移动。

循环队列判空：front == tail
循环队列判满：（tail+1）% c == front （其中c为数组的长度）
循环队列会默认浪费一个空间

2.6 循环队列接口

public interface Queue<E> {
    int getSize();
    boolean isEmpty();
    void enqueue(E e);
    E dequeue();
    E getFront();
}

2.7 循环队列的实现

import java.util.Arrays;

public class LooperQueue<E> implements Queue<E> {
    private E[] data;
    private int front,tail;
    private int size;

    public LooperQueue(int capacity) {
        data = (E[]) new Object[capacity +1];
        front = 0;
        tail = 0;
        size = 0;
    }

    public LooperQueue() {
        this(10);
    }

    @Override
    public boolean isEmpty() {
        return front == tail;
    }

    @Override
    public int getSize() {
        return size;
    }

    public int getCapacity() {
        return data.length - 1;
    }

    @Override
    public void enqueue(E e) {
        if((tail+1) % data.length == front) {
            resize(getCapacity()*2);
        }
        data[tail] = e;
        tail = (tail+1) % data.length;
        size++;
    }

    @Override
    public E dequeue() {
        if(isEmpty()) {
            throw new IllegalArgumentException("cannot dequeue");
        }

        E ret = data[front];
        data[front] = null;
        front = (front+1) % data.length;
        size--;
        if(size == getSize()/4 && getCapacity()/2!=0) {
            resize(getCapacity()/2);
        }

        return ret;
    }

    public E getFront() {
        if(isEmpty()) {
            throw new IllegalArgumentException("queue is Empty");
        }
        return data[front];
    }

    private void resize(int newCapacity) {
        E[] newData =  (E[]) new Object[newCapacity + 1];
        for(int i = 0; i<size; i++) {
            newData[i] = data[(front+i)%data.length];
        }

        data = newData;
        front = 0;
        tail = size;
    }

    @Override
    public String toString() {
        return "LooperQueue{" +
                "data=" + Arrays.toString(data) +
                ", front=" + front +
                ", tail=" + tail +
                ", size=" + size +
                '}';
    }
}

2.8 循环队列测试

public class Main {
    public static void main(String[] args) {
       LooperQueue<Integer> arrayQueue = new LooperQueue<>();
        for(int i=0; i<10; i++) {
            arrayQueue.enqueue(i);
            System.out.println(arrayQueue);

            if(i%3 == 2) {
                arrayQueue.dequeue();
                System.out.println(arrayQueue);
            }
        }
    }
}

2.9 循环队列与数组队列的比较

循环队列的复杂度分析：

void enqueue(E) O(1)
E dequeue() O(1)
E getFront() O(1)

循环队列在数组队列的基础上进行了优化，原因是由于数组队列的出队操作复杂度为O(n)，循环队列借助于一个指针指向队首和队尾位置，不需要像数组队列一样，每次有数据出队时均需要将后面的数据往前挪动，可以很灵活的将数据出队。

下面是一段用于测试循环队列与数组队列在进行100000个数据入队和出队时所消耗的时间程序：

import java.util.Random;

public class Main {
    public static void main(String[] args) {
            int opCount = 100000;
        	//测试数组队列
            ArrayQueue<Integer> arrayQueue = new ArrayQueue<>(opCount);
            double time1 = testQueue(arrayQueue,opCount);
            System.out.println(time1);
        	//测试循环队列
            LooperQueue<Integer> looperQueue = new LooperQueue<>(opCount);
            double time2 = testQueue(looperQueue,opCount);
            System.out.println(time2);
    }

    public static double testQueue(Queue<Integer> q,int opCount) {
        long startTime = System.nanoTime();
        Random random = new Random();
        //入队操作
        for(int i = 0; i<opCount; i++) {
            q.enqueue(random.nextInt(Integer.MAX_VALUE));
        }
		//出队曹组
        for(int i = 0; i<opCount; i++) {
            q.dequeue();
        }
        long endTime = System.nanoTime();
        return (endTime - startTime) / 1000000000.0;
    }
}

//测试结果，数组队列消耗21.797972269秒，循环队列消耗时间仅为0.013881263秒
21.797972269
0.013881263