核心思想
??本文提出一种快速的鲁棒的特征点匹配方法(GMS),其本质上是在现有的特征点匹配的基础上,筛除误匹配点,选择出更可靠的匹配点的方法,其作用类似RANSAC。其基于一个关键的假设——运动平滑性假设,即图像中相邻较近的属于同一个物体的特征点,在运动时也会一起运动,因此正确匹配点的邻域范围内应该还包含许多其他的匹配点,而误匹配点对应的位置可能是随机的,附近不会有很多的相邻匹配点。如下图所示
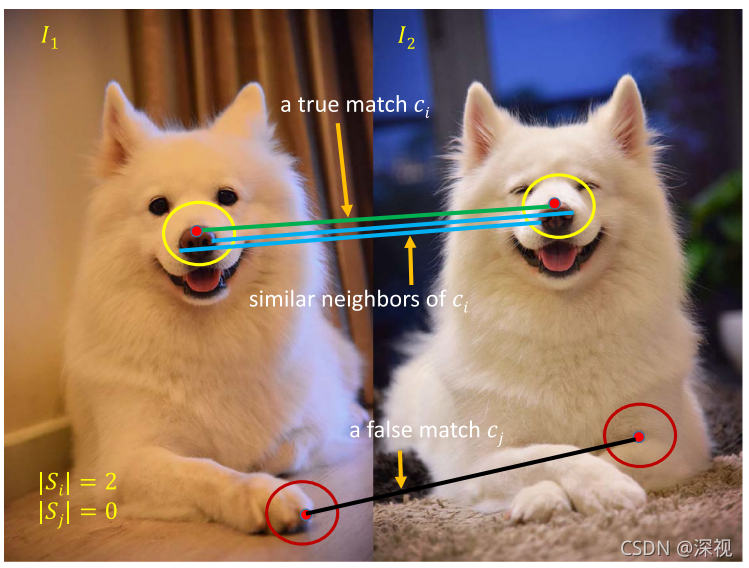
??基于上述的假设作者提出了基于网格的运动数据统计匹配方法(Grid-Based Motion Statistics,GMS)。首先,使用常见的特征点检测和匹配方法得到初始的匹配对集合
C
C
C,本文采用SIFT+最近邻匹配,并利用Ratio Test选出相对可靠的匹配点集合。对于匹配对集合中的一个匹配对
c
i
∈
C
c_i\in C
ci?∈C,其对应两幅图像中的两个匹配点
p
i
p_i
pi?和
q
i
q_i
qi?,其邻接特征点集合
N
i
N_i
Ni?的定义方式如下
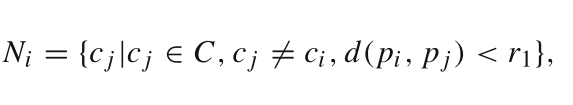
这个定义很简单了,就是在原图中与点
p
i
p_i
pi?的之间的距离小于
r
1
r_1
r1?的其他特征点,其对应的相似邻接特征点的集合
S
i
S_i
Si?的定义为
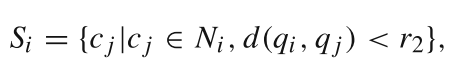
即在匹配图像中与点
p
i
p_i
pi?对应的匹配点
q
i
q_i
qi?之间的距离小于
r
2
r_2
r2?的特征点,简单来讲就是在原图中与目标特征点相邻,并且在匹配图像中也与目标特征点对应的匹配点相邻,即满足之前提到的运动平滑性假设的点。作者认为对于一对匹配点来说,其相似邻接特征点越多,其越可能是正确的匹配点。作者定义相似邻接特征点的数量
∣
S
i
∣
|S_i|
∣Si?∣为匹配对
c
i
c_i
ci?的"运动支持量"(motion support),其满足下述分布
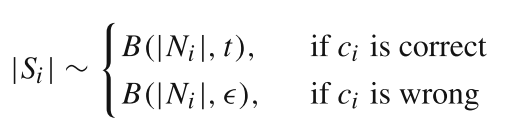
B
(
?
)
B(\cdot)
B(?)表示二项分布,
∣
N
i
∣
|N_i|
∣Ni?∣表示邻接特征点的数量,
t
t
t表示正确匹配的概率,
?
\epsilon
?表示误匹配的概率,则
∣
S
i
∣
|S_i|
∣Si?∣的期望和方差为
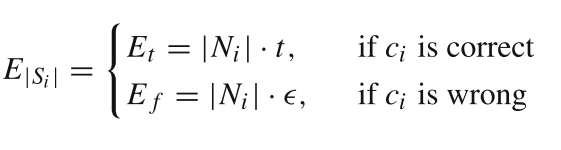
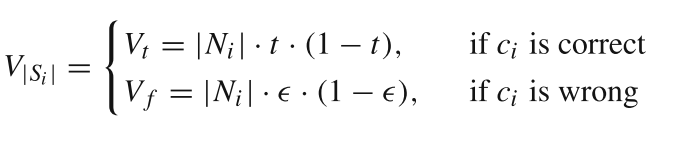
??根据上述公式,作者进一步定义真假匹配点分布之间的区分度得分为
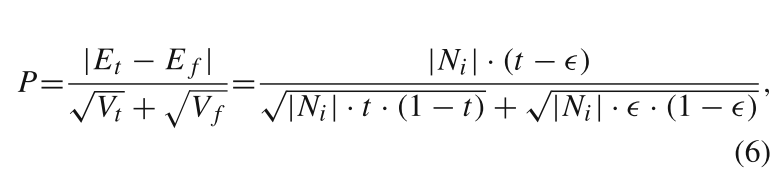
P
P
P值越大,则表示真假匹配点之间的区分度越大,而
P
P
P值与
∣
N
i
∣
\sqrt{|N_i|}
∣Ni?∣?成正比,即对于一个匹配点其相邻特征点数量越多,其判断得到匹配点的可靠性就越高。最后如何判断一个匹配对是正确的匹配对,文章只采用了一个简单的阈值
τ
i
\tau_i
τi?,如果
∣
S
i
∣
>
τ
i
|S_i|>\tau_i
∣Si?∣>τi?,则匹配对是正确匹配对,否则为错误匹配对,其中
τ
i
=
α
∣
N
i
∣
\tau_i=\alpha \sqrt{|N_i|}
τi?=α∣Ni?∣?,
α
\alpha
α通常取4~6。
??利用上述方法可以从候选匹配点中选择出可靠的匹配点,但是需要对候选匹配点集
C
C
C中的全部
N
N
N个匹配点都进行计算,而且计算过程中,每个匹配点还要计算与其他
N
?
1
N-1
N?1个特征点之间的距离,并判断匹配关系,因此算法的复杂度是
o
(
N
2
)
o(N^2)
o(N2)。作者通过划分网格的方法,使算法复杂度下降到
o
(
N
)
o(N)
o(N)。
??首先将图像划分成
m
?
m
m*m
m?m个不重叠的网格,如下图所示
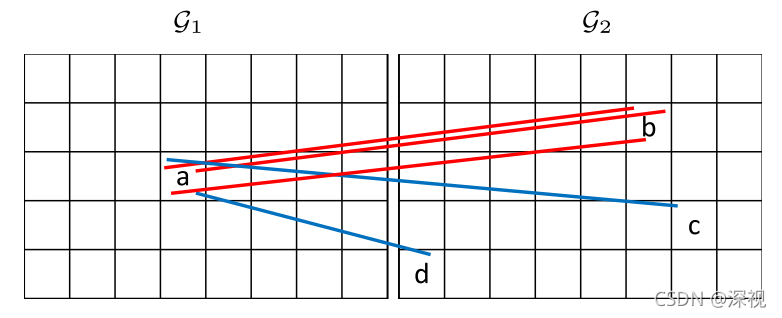
假设匹配对
c
i
c_i
ci?对应的两个匹配点在两幅图中分别位于方格
G
a
G_a
Ga?和
G
b
G_b
Gb?中,如图中红色的线条表示,那么
c
i
c_i
ci?的临界特征点集重新定义为
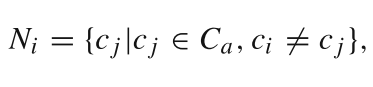
C
a
C_a
Ca?表示
G
a
G_a
Ga?中的全部特征点,与之前的定义不同,只需要和待匹配点处于同一个方格内就可以。同样的相似邻接特征点集可以定义为

C
a
b
C_{ab}
Cab?表示在原图中与待匹配点处于同一个方格,且在匹配图像中也与待匹配点对应的匹配点处于同一个方格中的特征点。简而言之,就是将之前通过计算两点之间的距离来判断相邻的过程,简化为了坐标是否处于同一个方格。此时计算一个匹配对的“运动支持量”只需要计算最优匹配方格对(如图中的
G
a
b
G_{ab}
Gab?)中的相似邻接特征点的数量,而不需要计算其他匹配方格对(如图中的
G
a
c
G_{ac}
Gac?和
G
a
d
G_{ad}
Gad?)中的相似邻接特征点的数量。
??如果方格的尺寸设定的太小,会导致每个方格内的邻接特征点数量过少,而如果方格的尺寸设定的太大,则会导致需要误匹配点也被包含在内。因此为了解决这个问题,作者又进一步提出了“运动核”(Motion Kernel)的概念,首先将方格的尺寸设定的小一些,在计算邻接特征点时不仅考虑当前方格内的点,还考虑该方格相邻的8个方格内的特征点,如下图所示
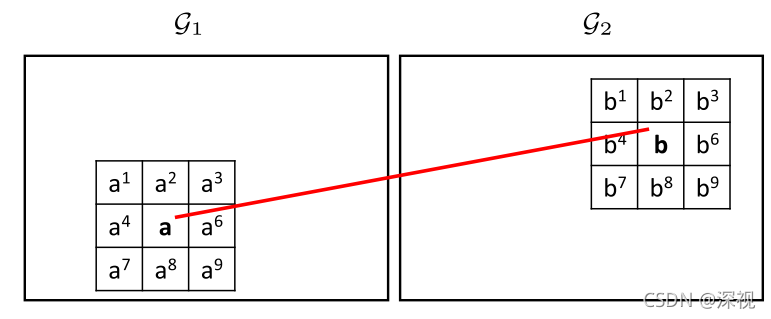
这样一来,邻接特征点集的定义和相似邻接特征点集的定义又改为如下方式
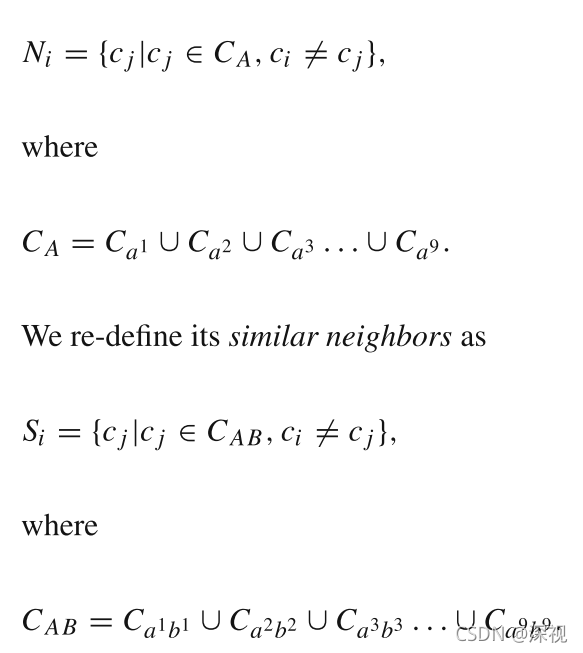
??匹配中还有一个关键的问题就是解决尺度变化和旋转问题。对于旋转问题,可以通过旋转匹配点相邻方格的方式来解决,如下图所示
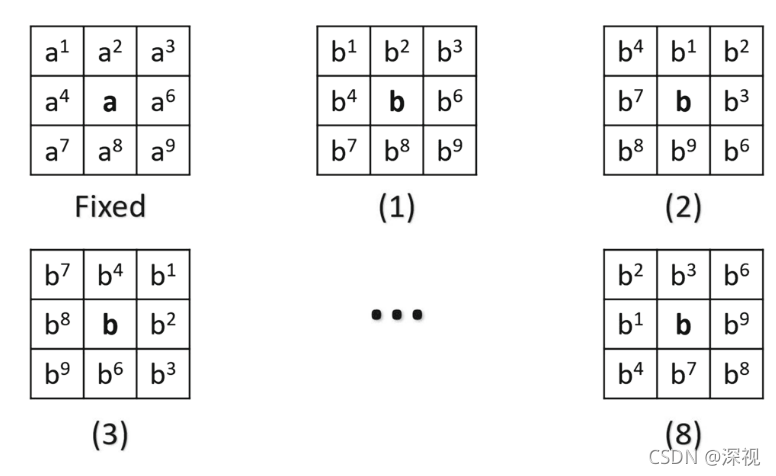
由上图可以看到,固定原图中的运动核不动,而匹配图像中对应的运动核是按照顺时针方向进行转动的,共有8个核对应8个旋转方向,可以从中选择出运动支持量最大的核作为最优匹配方格对。对于尺度变化问题,本文通过将匹配图像划分成不同尺寸的方格来解决,原图划分为
m
?
m
m*m
m?m个方格,而匹配图像划分成
α
m
?
α
m
\alpha m*\alpha m
αm?αm个方格,其中
α
\alpha
α可取
{
1
/
2
,
2
/
2
,
1
,
2
,
2
}
\{1/2, \sqrt{2}/2, 1, \sqrt{2},2\}
{1/2,2?/2,1,2?,2}五个值。
??整个算法的流程如下

创新点
- 利用运动平滑假设,从候选匹配点中选择出可靠的正确匹配点
- 通过划分网格的方法,降低算法复杂度
- 通过引入运动核的概念,解决了方格尺寸的设定,多尺度变化及旋转问题
算法评价
??该方法是一种简单且高效的特征匹配方法,整个算法思想并不复杂,但效果却十分显著。但本文的方法也存在一定的局限,在物体边缘位置的特征点不满足运动平滑性约束,但这部分点数量较小对于匹配结果影响有限。另一方面,本文适用于较为密集的特征点匹配,即候选匹配点数量越多,选择出的正确匹配点准确性也会越高,而当候选匹配点比较稀疏时,该方法效果就不好了。
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。