? ? ? ? 在最小二乘法和SVD优化中,简单的介绍了最小二乘法的基本原理和SVD优化的实现。但是对于单纯的二乘法而言对于噪声的学习经常会出现过拟合。为了避免其过拟合导致的模型过于复杂,可以通过给最小二乘法添加约束条件的方式来实现。下面将介绍两种常用的方法
部分空间约束的最小二乘法
? ? ? ? 对于由参数的线性模型
????????????????????????????????????????????????
? ? ? ? 其参数θ是可以自由设置的,所以使用的是全体的参数空间(即整个参数平面),如果对于参数空间的范围进行一定的限制,那么就可以有效的防止参数过拟合的现象发生。我们可以对参数附加一个Pθ=θ约束条件,而一样是求minJ(θ)。约束条件中的P是值域R(P)的正交投影矩阵。当参数和正交投影矩阵点积之后,获得向量将出于设定的值域R(P)中(这是正交投影矩阵的性质),从而起到限制了参数范围的效果。这么做可以只使用参数空间的一部分,不过相对的设置P的自由度会很大。正交投影矩阵的性质是满足P^2=P和P'=P的b*b矩阵。我们将普通的最小二乘法计算θ中的Φ附加一个P,令公式变为:
???????????????????????????????????????????????????????
P的值并不是固定的,需要根据情况进行调整。下面我们使用空间约束的最小二乘法来对(1,sin(x/2),cos(x2),...sin(15/2*x),cos(15/2*x))来进行拟合。
"""
部分空间约束的最小二乘法
@author:茱莉亚之歌
"""
import numpy as np
import matplotlib.pyplot as plt
def theta(x,y):
return np.dot(np.linalg.pinv(x),y)
#生成待拟合的数据
n=50
N=1000
x=np.linspace(-3,3,n)
X=np.linspace(-3,3,N)
p=np.zeros((n,31))
P=np.zeros((N,31))
p[:,0:0]=np.ones(n).reshape(-1,1)
P[:,0:0]=np.ones(N).reshape(-1,1)
for i in range(0,15):
p[:,2*i+1]=np.sin(i/2*x)
p[:,2*i]=np.cos(i/2*x)
P[:,2*i+1]=np.sin(i/2*X)
P[:,2*i]=np.cos(i/2*X)
y=np.sinc(x)+0.1*x+0.2*np.random.randn(n)
#载入正交投影矩阵
OPM=np.zeros((31,31))
OPM[0:11,0:11]=np.diag(np.ones(11))
plt.plot(x,y,'b.')
plt.plot(X,np.dot(P,theta(p,y)))
plt.plot(X,np.dot(P,theta(np.dot(p,OPM),y)),'g')
plt.axis([-3,3,-1,1.5])
plt.show()
拟合的结果图
??????????????????????????????????????
?可以看出,相比于没有进行参数约束的拟合,约束参数可以明显的改善模型过拟合的情况。
L2约束的最小二乘法
? ? ? ? L2约束相对于上面的部分空间约束在参数上的操作相对容易。它同样也是通过附加条件来实现的约束,附加条件为:
????????????????????????????????????????????????????????????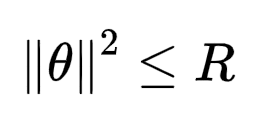
?和部分空间约束类似,它将参数的范围限制到了一个类似圆形的区域中,让求解J(θ)最优值的问题变成了一个拉格朗日对偶问题。那么我们就可以使用拉格朗日乘子和拉格朗日函数来进行求解。拉格朗日函数的形式为L(t,λ)=f(t)+λ'g(t),其中λ称作拉格朗日乘子。由此可以得到下面的式子,其约束条件是λ>=0。(由于计算和θ相关微分的时候会产生乘数2,所以这里使用的是λ/2)
?????????????????????????????????????????????????????
?那么我们可以对其求微分得到:
??????????????????????????????????????????????????????
?即:
????????????????????????????????
它和普通的最小二乘法的求参数公式非常像,但是其加入了一个正则化矩阵以提高其正则性,进而可以更稳定地进行逆矩阵地求解。那么我们尝试利用L2约束来进行最小二乘法的拟合,正则化参数这里取0.1,拟合的依然是上面的(1,sin(x/2),cos(x2),...sin(15/2*x),cos(15/2*x))。
"""
L2约束的最小二乘法
@author:茱莉亚之歌
"""
import numpy as np
import matplotlib.pyplot as plt
def theta(x,y):
return np.dot(np.linalg.pinv(x),y)
#生成待拟合的数据
n=50
N=1000
x=np.linspace(-3,3,n)
X=np.linspace(-3,3,N)
y=np.sinc(x)+0.1*x+0.2*np.random.randn(n)
p=np.zeros((n,31))
P=np.zeros((N,31))
p[:,0:0]=np.ones(n).reshape(-1,1)
P[:,0:0]=np.ones(N).reshape(-1,1)
for i in range(0,15):
p[:,2*i+1]=np.sin(i/2*x)
p[:,2*i]=np.cos(i/2*x)
P[:,2*i+1]=np.sin(i/2*X)
P[:,2*i]=np.cos(i/2*X)
#设置L2约束的参数
l=0.1
L2=np.dot(p.T,p)+l*np.eye(31)
plt.plot(x,y,'b.')
plt.plot(X,np.dot(P,theta(p,y)))
plt.plot(X,np.dot(P,theta(L2,np.dot(p.T,y))),'g')
plt.axis([-3,3,-1,1.5])
plt.show()拟合结果如下:
??????????????????????? ?
?
?可以看出,L2约束也很好的防止了模型过拟合。
本文为个人学习笔记,如有问题欢迎讨论和指出@茱莉亚之歌