Apriori---[?pri??ri] ---先天的,推测的
一、相关概念:
关联分析,是一门分析技术,用于发现大量数据中,各组数据之间的联系。
{X}的支持度 = {X}在事务中出现的次数 / 事务总数
关联规则{X}→{Y}的置信度 = {X,Y}的支持度 / {X}的支持度
{X}→{Y}的提升度 = {X}→{Y}的置信度 / {Y}的支持度

以上图交易订单为例:
1、事务:每条交易记录可称为一个事务,所以,这份交易数据一共含有4条“事务”。
2、项:交易中的不同物品可称为一个项。所以,这4条交易记录,一共含有4个项(商品类目):“薯条”,“可乐”,“奶茶”,“汉堡”。
3、项集:0个或多个项的集合,可称为一个项集,一般用{X}的形式表示项集,k 个项组成的项集,叫 k 项集。如{薯条,可乐}(2 项集),{薯条}(1 项集)。
上面的4项商品,可以相互组成15个项集,项集内不存在相同的项,如{奶茶,薯条,薯条}。如下:

4、支持度:不同“项集”,受顾客的欢迎程度不同。支持度(Support)可以表示项集在事务中出现的概率(频率),也可以理解成顾客对某一个项集的“支持程度”。
support--- [s??p??t] ---支持
{X}的支持度 = {X}在事务中出现的次数 / 事务总数。

如上图,奶茶在4个事务中共出现了一次,那么奶茶的支持度为1/4=0.25
奶茶、薯条在4个事务中共出现了一次,那么奶茶、薯条的支持度为1/4=0.25
每个项集都有支持度,但事实上,也不是每个项集都是有用的。
比如支持度为0的 4 项集:{可乐,汉堡,奶茶,薯条},客人都没买过这样的套餐,就没有指导价值。
5、最小支持度:此时,我们需要人为地设定一个支持度,名为最小支持度,用于筛掉那些不符合需求的项集。被留下来的项集(≥ 最小支持度),被称为频繁项集。有了频繁项集,就可以生产关联规则了。
6、关联规则:关联分析是探索数据之间联系的技术,而数据之间的联系,我们用关联规则来表示,表达式为:{X}→{Y}(X 和 Y 之间不存在相同项)。
规则有顺序之分,为了方便描述,我们把规则前面的项集叫前件,把规则后面的项集叫后件。
假设有频繁项集 {奶茶,薯条},(这里奶茶为前件,薯条为后件),它可以生成2条关联规则:{奶茶}→{薯条}和{薯条}→{奶茶}。前者的意思是,购买“奶茶”的顾客,和购买“薯条”之间,可能存在有某种联系!
7、置信度(Confidence):[?kɑ?nf?d?ns] —信心
置信度(Confidence)可用于衡量关联规则的可靠程度,表示在前件出现的情况下,后件出现的概率。一般来说,概率越高,规则的可靠性越强。
关联规则{X}→{Y}的置信度 = {X,Y}的支持度 / {X}的支持度。

在实际业务中,也需要人为地设定置信度,名为最小置信度,用于筛掉一些不符合需求的关联规则。
被留下来的关联规则( ≥ 最小置信度),叫做强关联规则。
8、提升度:关联规则既有促进关系,也有抑制关系。因而,还需引入提升度(Lift)对它们进行判断。Lift— [l?ft]—举起、电梯;
{X}→{Y}的提升度 = {X}→{Y}的置信度 / {Y}的支持度,意思是评估 X 的出现,对 Y 出现的影响有多大。

提升度的值小于1,表示前件对后件是抑制的关系;
提升度大于1,表示前件对后件是促进的关系;
特别地,当提升度的值等于1时,表示前件不影响后件,两者之间没有关系。
概念总结:

大多数的关联分析工作,主要任务就是生成频繁项集和关联规则。
一个3项(k 项)的数据集,能产生7(2^k - 1)个非空频繁项集。
一个3项(k 项)的频繁项集,可产生6(2^k - 2)个关联规则。

二、Apriori 算法
2.1、确定最小支持度和最小置信度
最小支持度和最小置信度都是描述事件发生的概率,所以取值范围在 0 和 1 之间。
假如最小支持度设定过高,就会导致一些重要但不频繁的项集被过滤掉;设定过低,一方面,会影响计算性能,另一方面,一些无实际意义的数据也会被保留下来,最小置信度也是同理。
但判断它们是否“合适”的感觉很微妙,没有特定的标准答案,可以根据过往经验、试错法、事务出现的最小频率等去思考,总结起来就一个字:试。
一开始设定的最小支持度和置信度和理想状态有一定偏差也没关系,后续再慢慢调整。
如下,倘若我现在确定的最小支持度为0.2,最小置信度为0.7,

2.2、找出频繁项集和强关联规则
这一步,Apr 的算法主要依赖两个性质:
1)一个项集如若是频繁的,那它的非空子集也一定是频繁的。假如购买{薯条,奶茶}的概率都很高,那购买{薯条}或{奶茶}的概率肯定也很高。
2)一个项集如若是非频繁的,那包含该项集的项集也一定是非频繁的。假设购买{薯条}的次数少,那购买{薯条,奶茶}的次数肯定也少。
Apr 算法一旦找到某个不满足条件的“非频繁项集”,包含该集合的其他项集不需要计算,更不用对比,通通绕开。
比如,在对比2项集的时候,发现{奶茶,汉堡}的支持度为 0,小于最小支持度0.2,属于非频繁项集。于是,后面在计算3项集(及4项集)的时候,会直接把包含{奶茶,汉堡}的项集,如{薯条,奶茶,汉堡}去掉,不再计算。以此类推,直到算到最后一层项集,所有的频繁项集才算筛选完毕。
凭借新生成的频繁项集,就可以开始“制造”关联规则了。
因为频繁 1 项集只有一个项,无法构成具有指导意义的关联关系(≥ 2 项),可直接忽略。
现抽取其中一个频繁 3 项集{薯条,可乐,汉堡},进入关联规则的生产环节。
Apr 算法会先产生一系列后件项数为1的关联规则,与最小置信度进行比较,得到一部分强关联规则。

然后,频繁项集继续生成后件的项数为2的关联规则,再对它们的置信度进行比较,又收获一批强关联规则。

当无法从剩下的频繁项集中生成新的关联规则时,该过程就结束了。
通过这种方式,其他的频繁项集也加入到关联规则的“生产线”上,最终通过最小置信度筛选,就算“牵手”成功,得到强关联规则如下:

若是这些强关联规则正好是你想要的,那就进一步计算它们的提升度。
相反,若是你对筛选出来的强关联规则不满意,那我们就得重新调整最小支持度和最小置信度,再计算一次。
2.3、Python 调用 apriori 函数
尽管 Apr 算法已经对原始的关联分析做了优化,但手动计算依然繁琐,特别是当我们想要调整最小支持度或者最小置信度的时候。
如果能把 Apr 算法的计算流程抽象成函数,将最小支持度、最小置信度和最小提升度设置成参数,通过调整参数来查看关联规则,想怎么调就怎么调,那就最好了。实际上,Python 已经实现了这一切,那就是apriori函数
apyori模块属于 Python 的第三方模块,在本地使用它,需要先安装一下。
apriori函数常用的参数有4个:transactions(事务的集合),min_support(最小支持度),min_confidence(最小置信度),min_lift(最小提升度)。

现将前面的快餐店事务整合成了嵌套列表orders,调用apriori函数,传入参数:orders,最小支持度为0.2,最小置信度为0.7。并查看返回结果。在不传min_lift值的情况下,将使用它的默认值0.0
In [ 33 ]
?
1# 导入 apyori 模块下的 apriori 函数
2 from apyori import apriori
3 # 创建4条快餐交易数据
4 orders = [['薯条', '可乐'], ['薯条', '可乐', '奶茶'], ['汉堡', '薯条', '可乐'], ['汉堡', '可乐']]
5 # 创建变量 results,调用 apriori 函数,传入参数:orders,最小支持度为 0.2,最小置信度为 0.7
6 results = apriori(orders,min_support=0.2,min_confidence=0.7)
7 # 查看变量 results
8 results
Out [ 33 ]
<generator object apriori at 0x7fa21646ec50>
generator--- [?d?en?re?t?(r)] ---发电机
generato是一个生成器对象,它是一种用于节省空间的运算机制,可以通过循环遍历的形式对它里面的数据进行访问:
relation---[r??le??n]---关系, Record--- [?rek??d , r??k??d] ---记录
In [ 35 ]
1 # 调用 apriori 函数
2 results = apriori(orders, min_support=0.2, min_confidence=0.7)
3 # 查看变量 results
4 for result in results:
5 print(result)
运行
Out [ 35 ]
RelationRecord(items=frozenset({'可乐'}), support=1.0, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'可乐'}), confidence=1.0, lift=1.0)])
RelationRecord(items=frozenset({'薯条'}), support=0.75, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'薯条'}), confidence=0.75, lift=1.0)])
RelationRecord(items=frozenset({'可乐', '奶茶'}), support=0.25, ordered_statistics=[OrderedStatistic(items_base=frozenset({'奶茶'}), items_add=frozenset({'可乐'}), confidence=1.0, lift=1.0)])
RelationRecord(items=frozenset({'可乐', '汉堡'}), support=0.5, ordered_statistics=[OrderedStatistic(items_base=frozenset({'汉堡'}), items_add=frozenset({'可乐'}), confidence=1.0, lift=1.0)])
RelationRecord(items=frozenset({'可乐', '薯条'}), support=0.75, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'可乐', '薯条'}), confidence=0.75, lift=1.0), OrderedStatistic(items_base=frozenset({'可乐'}), items_add=frozenset({'薯条'}), confidence=0.75, lift=1.0), OrderedStatistic(items_base=frozenset({'薯条'}), items_add=frozenset({'可乐'}), confidence=1.0, lift=1.0)])
RelationRecord(items=frozenset({'薯条', '奶茶'}), support=0.25, ordered_statistics=[OrderedStatistic(items_base=frozenset({'奶茶'}), items_add=frozenset({'薯条'}), confidence=1.0, lift=1.3333333333333333)])
RelationRecord(items=frozenset({'可乐', '薯条', '奶茶'}), support=0.25, ordered_statistics=[OrderedStatistic(items_base=frozenset({'奶茶'}), items_add=frozenset({'可乐', '薯条'}), confidence=1.0, lift=1.3333333333333333), OrderedStatistic(items_base=frozenset({'可乐', '奶茶'}), items_add=frozenset({'薯条'}), confidence=1.0, lift=1.3333333333333333), OrderedStatistic(items_base=frozenset({'薯条', '奶茶'}), items_add=frozenset({'可乐'}), confidence=1.0, lift=1.0)])
RelationRecord(items=frozenset({'可乐', '薯条', '汉堡'}), support=0.25, ordered_statistics=[OrderedStatistic(items_base=frozenset({'薯条', '汉堡'}), items_add=frozenset({'可乐'}), confidence=1.0, lift=1.0)])
又出来一大堆“不明所以”的数据。
运行结果一共有 8 条 RelationRecord(关系记录),现抽取其中一条,简单说明一下:

RelationRecord(关系记录)和 OrderedStatistic(有序的统计数据)是模块作者自定义的命名元组(namedtuple),可以理解成一种通过名称访问的元组。
而frozenset是一种不可变的集合,使用list()函数,可以将它转换成我们熟悉的列表形态。
然后,我们再来了解一下数据的结构:
一条“关系记录”(RelationRecord),包含了频繁项集的基本信息:频繁项集items,支持度support和统计列表ordered_statistics。
一条“统计列表”(ordered_statistics),包含了该频繁项集下构建的所有强关联规则OrderedStatistic。
一条“强关联规则”(OrderedStatistic),包含了该规则的基本信息:前件items_base,后件items_add,置信度confidence,提升度lift。
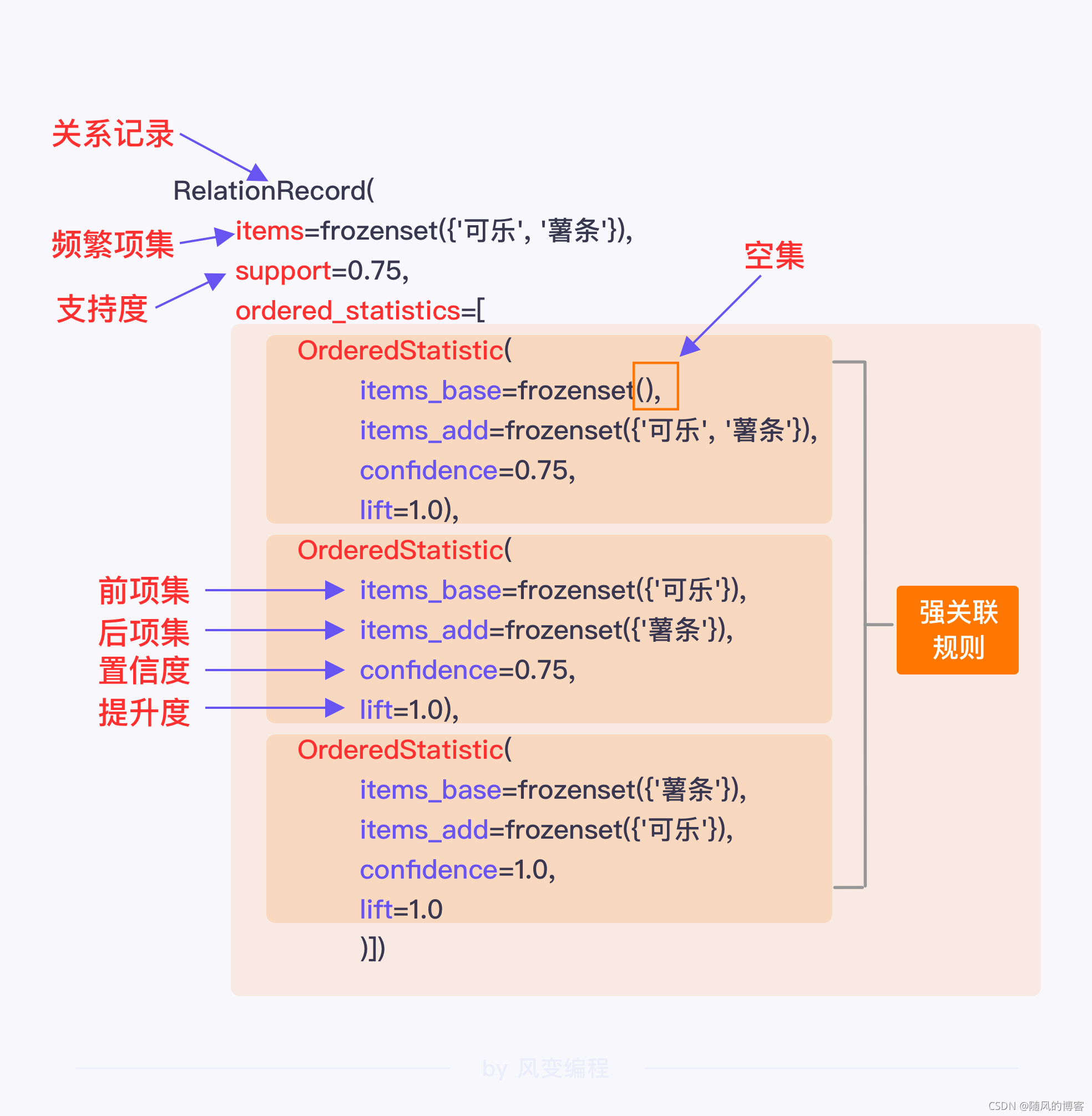
这里还需要进一步抽取关键信息。
抽取的重点,是由前件和后件组成的强关联规则,以及它们的支持度、置信度、提升度。
方法就像剥洋葱,一层一层地剥它就对了!若找到前件为空集的强关联规则,那么,这条规则其实没有什么现实意义,可直接删除。
In [ 36 ]
1 # 调用 apriori 函数
2 results = apriori(orders, min_support=0.2, min_confidence=0.7)
3 # 遍历结果数据
4 for result in results:
5 # 获取支持度,并保留3位小数
6 support = round(result.support, 3)
7
?
8 # 遍历ordered_statistics对象
9 for rule in result.ordered_statistics:
10
# 获取前件和后件并转成列表
11 head_set = list(rule.items_base)
12 tail_set = list(rule.items_add)
13
?
14 # 跳过前件为空的数据
15 if head_set == []:
16 continue
17
?
18 # 将前件、后件拼接成关联规则的形式
19 related_catogory = str(head_set)+'→'+str(tail_set)
20
?
21 # 提取置信度,并保留3位小数
22 confidence = round(rule.confidence, 3)
23
# 提取提升度,并保留3位小数
24 lift = round(rule.lift, 3)
25
?
26 # 查看强关联规则,支持度,置信度,提升度
27 print(related_catogory, support, confidence, lift)
运行
Out [ 36 ]
['奶茶']→['可乐'] 0.25 1.0 1.0
['汉堡']→['可乐'] 0.5 1.0 1.0
['可乐']→['薯条'] 0.75 0.75 1.0
['薯条']→['可乐'] 0.75 1.0 1.0
['奶茶']→['薯条'] 0.25 1.0 1.333
['奶茶']→['可乐', '薯条'] 0.25 1.0 1.333
['可乐', '奶茶']→['薯条'] 0.25 1.0 1.333
['薯条', '奶茶']→['可乐'] 0.25 1.0 1.0
['薯条', '汉堡']→['可乐'] 0.25 1.0 1.0
end