2021年9月广州羊城杯,CRYPTO的BigRsa
下载附件,pub.py:

.
.
打开文件,发现内容是RSA加密过程:
from Crypto.Util.number import *
from flag import *
n1 = 103835296409081751860770535514746586815395898427260334325680313648369132661057840680823295512236948953370895568419721331170834557812541468309298819497267746892814583806423027167382825479157951365823085639078738847647634406841331307035593810712914545347201619004253602692127370265833092082543067153606828049061
n2 = 115383198584677147487556014336448310721853841168758012445634182814180314480501828927160071015197089456042472185850893847370481817325868824076245290735749717384769661698895000176441497242371873981353689607711146852891551491168528799814311992471449640014501858763495472267168224015665906627382490565507927272073
e = 65537
m = bytes_to_long(flag)
c = pow(m, e, n1)
c = pow(c, e, n2)
print("c = %d" % c)
# output
# c = 60406168302768860804211220055708551816238816061772464557956985699400782163597251861675967909246187833328847989530950308053492202064477410641014045601986036822451416365957817685047102703301347664879870026582087365822433436251615243854347490600004857861059245403674349457345319269266645006969222744554974358264
.
.
.
(这里积累第一个经验)
首先回顾一下以前的积累的RSA知识:

.
.
然后搬出以前自己写的RSA脚本参考一下,回顾libnum.invmode函数和pow函数以及long_to_bytes函数的作用。
d = libnum.invmod(e, (p - 1) * (q - 1))
#invmod(a, n) - 求a对于n的模逆,这里逆向加密过程中计算ψ(n)=(p-1)(q-1),对ψ(n)保密,也就是对应根据e*d=1modψ(n),求出d
.
m = pow(c, d, n)
#这里的m是十进制形式,pow(x, y[, z])–函数是计算 x 的 y 次方,如果 z 在存在,则再对结果进行取模,其结果等效于 pow(x,y) %z,对应前面解密算法中M=D?=(C^d)mod n
.
string = long_to_bytes(m)# 获取m明文
.
.
然后回到羊城杯的题目你就会发现,题目先用公共模数n1对flag m加密一次,再用公共模数n2对RSA一次加密后的密文再加密一次,这是两层加密:

.
.
按理来说两层常规的RSA解密即可,关键就是这里的n1、n2太大了,无法硬分解,常规的分解素数网站没法用。

.
.
(这里积累第二个经验)
然后就去查资料了,因为RSA自己也不在行,下面是从博客https://blog.csdn.net/huanghelouzi/article/details/82943615中找到的。
RSA小指数e攻击
如果RSA系统的公钥e选取较小的值,可以使得加密和验证签名的速度有所提高,但是如果e的选取太小,就容易受到攻击。
.
有三个分别使用不同的模数n1,n2,n3,但是都选取e=3,加密同一个明文可以得到:
.
c1 = pow(m,3,n1)
c2 = pow(m,3,n2)
c3 = pow(m,3,n3)
.
一般情况下,n1,n2,n3互素,否则会比较容易求出公因子,从而安全性大幅度的减低。
.
利用公约数
如果两次加密的n1和n2具有相同的素因子,可以利用欧几里德算法直接分解n1和n2.
通过欧几里德算法计算出两个n的最大公约数p:
def gcd(a, b):
if a < b:
a, b = b, a
while b != 0:
temp = a % b
a = b
b = temp
def gcd_digui(a, b):
if b != 0:
return a
return gcd(b,a%b)
p = gcd(n1,n2)
.
识别
识别此类题目,通常会发现题目给了若干个n,均不相同,并且都是2048bit,4096bit级别,无法正面硬杠,并且明文都没什么联系,e也一般取65537。
.
根据欧几里德算法算出的p之后,再用n除以p即可求出q,由此可以得到的参数有p、q、n、e,再使用常规方法计算出d,即可破解密文。
.
.
.
和题目八九不离十,那这道bigrsa就是这样解的了,用两个公共模数n来求公因子。
在此之前中间还有个小插曲,那就是CTF-RSA-tool工具,一开始我以为这中两个n、一个e、一个c的是CTF-RSA-tool工具中example的模不互素:(下面是我以前的笔记)

.
.
(这里积累第三个经验)
后来怎么跑都跑不出来,看了工具内对应代码才发现模不互素是给你两个单独分解不了的大数级n,方便让你求公因子。然后,只用一个n来加密,对,只用一个n。(我也是现在才理解模不互素的内容)

.
.
前面博客的欧几里德算法脚本不太会用,所以直接抽出CTF-RSA-tool工具的这段脚本来用算了,因为上面的求公因子代码已经写好了,只要再加多一层解密即可,脚本如下
import gmpy2
def share_factor(n1, n2, e, c1):
p1 = gmpy2.gcd(n1, n2)
q1 = n1 / p1
q2 = n2 / p1
d1 = gmpy2.invert(e, (p1 - 1) * (q1 - 1))
plain = gmpy2.powmod(c1, d1, n1)
d2 = gmpy2.invert(e, (p1 - 1) * (q2 - 1))
plain = gmpy2.powmod(plain, d2, n2)
plain = hex(plain)[2:]
if len(plain) % 2 != 0:
plain = '0' + plain
print('Here are your plain text: \n' + plain.decode('hex'))
if __name__ == "__main__":
n1 = 115383198584677147487556014336448310721853841168758012445634182814180314480501828927160071015197089456042472185850893847370481817325868824076245290735749717384769661698895000176441497242371873981353689607711146852891551491168528799814311992471449640014501858763495472267168224015665906627382490565507927272073
n2 = 103835296409081751860770535514746586815395898427260334325680313648369132661057840680823295512236948953370895568419721331170834557812541468309298819497267746892814583806423027167382825479157951365823085639078738847647634406841331307035593810712914545347201619004253602692127370265833092082543067153606828049061
e = 65537
c1 = 60406168302768860804211220055708551816238816061772464557956985699400782163597251861675967909246187833328847989530950308053492202064477410641014045601986036822451416365957817685047102703301347664879870026582087365822433436251615243854347490600004857861059245403674349457345319269266645006969222744554974358264
share_factor(n1, n2, e, c1)
.
.
结果:(用python2跑)

.
.
最后附上别人WP的脚本(只能截图了):不同在于我的脚本直接用p1 = gmpy2.gcd(n1, n2)取公因子,而他使用自定义gcd函数求公约数,就是利用了前面的欧几里得算法。
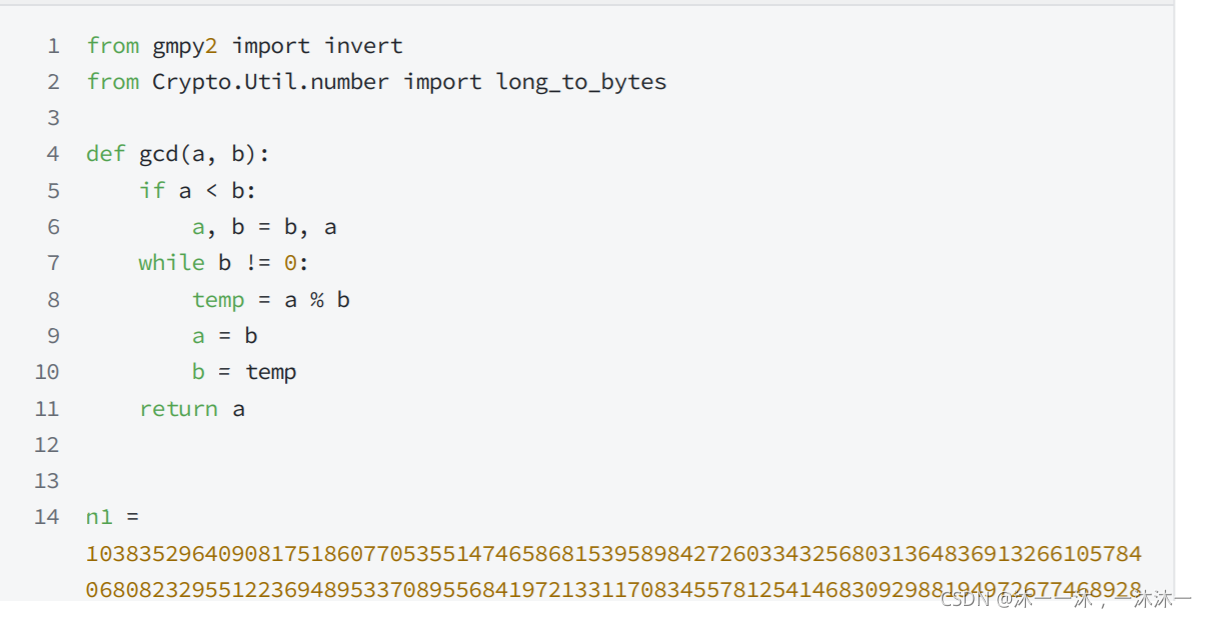

.
.
总结:
1:
(这里积累第一个经验) 首先回顾一下以前的积累的RSA知识:
.
.
然后搬出以前自己写的RSA脚本参考一下,回顾libnum.invmode函数和pow函数以及long_to_bytes函数的作用。
d = libnum.invmod(e, (p - 1) * (q - 1))
#invmod(a, n) - 求a对于n的模逆,这里逆向加密过程中计算ψ(n)=(p-1)(q-1),对ψ(n)保密,也就是对应根据e*d=1modψ(n),求出d
.
m = pow(c, d, n)
#这里的m是十进制形式,pow(x, y[, z])–函数是计算 x 的 y 次方,如果 z 在存在,则再对结果进行取模,其结果等效于 pow(x,y) %z,对应前面解密算法中M=D?=(C^d)mod n .string = long_to_bytes(m)# 获取m明文
2:
(这里积累第二个经验)
然后就去查资料了,因为RSA自己也不在行,下面是从博客https://blog.csdn.net/huanghelouzi/article/details/82943615中找到的。RSA小指数e攻击 如果RSA系统的公钥e选取较小的值,可以使得加密和验证签名的速度有所提高,但是如果e的选取太小,就容易受到攻击。 .
有三个分别使用不同的模数n1,n2,n3,但是都选取e=3,加密同一个明文可以得到: . c1 = pow(m,3,n1) c2 =
pow(m,3,n2) c3 = pow(m,3,n3) .
一般情况下,n1,n2,n3互素,否则会比较容易求出公因子,从而安全性大幅度的减低。 .
利用公约数 如果两次加密的n1和n2具有相同的素因子,可以利用欧几里德算法直接分解n1和n2. 通过欧几里德算法计算出两个n的最大公约数p:
def gcd(a, b):
if a < b:
a, b = b, a
while b != 0:
temp = a % b
a = b
b = temp
def gcd_digui(a, b):
if b != 0:
return a
return gcd(b,a%b)
p = gcd(n1,n2)
.
识别
识别此类题目,通常会发现题目给了若干个n,均不相同,并且都是2048bit,4096bit级别,无法正面硬杠,并且明文都没什么联系,e也一般取65537。
.
根据欧几里德算法算出的p之后,再用n除以p即可求出q,由此可以得到的参数有p、q、n、e,再使用常规方法计算出d,即可破解密文。
3:
(这里积累第三个经验)
后来怎么跑都跑不出来,看了工具内对应代码才发现模不互素是给你两个单独分解不了的大数级n,方便让你求公因子。然后,只用一个n来加密,对,只用一个n。(我也是现在才理解模不互素的内容)
.
.
前面博客的欧几里德算法脚本不太会用,所以直接抽出CTF-RSA-tool工具的这段脚本来用算了,因为上面的求公因子代码已经写好了,只要再加多一层解密即可。
解毕!敬礼!