本文主要参考:
- GB/T 4882-2001《数据的统计处理和解释正态性检验》;
- A test for normality based on the empirical characteristic function;作者: T. W. EPPS,年份:1983;
- An approximation to the limit distribution of the epps-pulley test statistic for normality; 作者:henze,年份:1990;
- Recent and classical tests for normality - a comparative study;作者:henze;年份:1989
原理介绍
随机变量
X
1
,
X
2
,
?
?
,
X
n
X_1, X_2, \cdots, X_n
X1?,X2?,?,Xn? 来同一总体分布
F
(
x
)
F(x)
F(x),其经验特征函数为
Φ
n
(
t
)
=
n
?
1
∑
j
exp
?
(
i
t
X
j
)
\Phi_n (t) = n^{-1} \sum_j \exp(i t X_j)
Φn?(t)=n?1∑j?exp(itXj?),其中
t
t
t 是一个
任意取值的实值参数,经验特征函数总会收敛于总体的特征函数
Φ
(
t
)
\Phi(t)
Φ(t)。总体分布
F
(
x
)
F(x)
F(x) 与特征函数
Φ
(
t
)
\Phi(t)
Φ(t) 呈一一对应的关系(特征函数是总体的概率密度函数的傅里叶变换),因此可以考虑使用经验特征函数
Φ
n
(
t
)
\Phi_n(t)
Φn?(t) 做为检验统计量,来判断总体分布
F
(
x
)
F(x)
F(x) 是否为正态分布。
小知识:总体累计分布函数 F ( x ) F(x) F(x) 对应样本的经验分布函数 F n ( x ) = n ? 1 ∑ j I ( X j ≤ x ) F_n(x)=n^{-1} \sum_j I(X_j \leq x) Fn?(x)=n?1∑j?I(Xj?≤x);
同样的,总体的特征函数 Φ ( t ) \Phi(t) Φ(t) 也对应样本的经验分布函数 Φ n ( t ) = n ? 1 ∑ j ( i t X j ) \Phi_n(t) = n^{-1} \sum_j (i t X_j) Φn?(t)=n?1∑j?(itXj?)
在正态分布的情况下,总体特征函数为 Φ 0 ( t ) = exp ? ( i t μ ? 1 / 2 t 2 σ 2 ) \Phi_0(t) = \exp(i t \mu - 1/2 t^2 \sigma^2) Φ0?(t)=exp(itμ?1/2t2σ2),其中 μ , σ 2 \mu, \sigma^2 μ,σ2 为均值和方差。于是可以将检验统计量取值为,对区间 t 范围内的 Φ n ( t ) ? Φ ^ 0 ( t ) \Phi_n(t) - \hat{\Phi} _0(t) Φn?(t)?Φ^0?(t) 平方模加权, Φ ^ 0 ( t ) = exp ? ( i t μ ? 1 / 2 t 2 σ 2 ) \hat{\Phi}_0(t) = \exp(i t \mu - 1/2 t^2 \sigma^2) Φ^0?(t)=exp(itμ?1/2t2σ2),此时的 μ , σ \mu, \sigma μ,σ 为样本的均值和方差的估计。
具体如下:
T
n
=
∫
?
∞
∞
∣
Φ
n
(
t
)
?
Φ
^
0
(
t
)
∣
2
d
G
(
t
)
T_n = \int_{-\infty}^{\infty} |\Phi_n(t) - \hat{\Phi}_0 (t) |^2 d G(t)
Tn?=∫?∞∞?∣Φn?(t)?Φ^0?(t)∣2dG(t)
其中
Φ
^
n
(
t
)
=
exp
?
(
i
t
X
ˉ
?
1
/
2
t
2
S
2
)
\hat{\Phi}_n(t)=\exp(it \bar{X} - 1/2 t^2 S^2)
Φ^n?(t)=exp(itXˉ?1/2t2S2),
X
ˉ
\bar{X}
Xˉ 为样本均值,
S
2
S^2
S2为样本的二阶中心矩,
S
2
=
∑
j
=
1
n
(
X
j
?
X
ˉ
)
2
n
S^2 = \frac{\sum_{j=1}^n(X_j - \bar{X})^2}{n}
S2=n∑j=1n?(Xj??Xˉ)2?。
权重系数 G ( t ) G(t) G(t) 的选择应符合如下要求:
- 对 ∣ Φ 1 ( t ) ? Φ 0 ( t ) ∣ |\Phi_1(t) - \Phi_0(t)| ∣Φ1?(t)?Φ0?(t)∣ 赋予大系数。这是因为 Φ 1 ( t ) \Phi_1(t) Φ1?(t) 属于多数备择假设。若输入标准化形式(减均值除方差),则多数的连续型分布在区间 t ∈ ( 0 , 3 ) t\in(0,3) t∈(0,3) 下, ∣ Φ 1 ( t ) ? Φ 0 ( t ) |\Phi_1(t)- \Phi_0(t) ∣Φ1?(t)?Φ0?(t) 都是很大的。
- 当
Φ
n
(
t
)
\Phi_n(t)
Φn?(t) 是对
Φ
(
t
)
\Phi(t)
Φ(t) 的精确拟合时,赋予较大权重。根据:
E { ∣ Φ n ( t ) ? Φ ( t ) ∣ 2 } = n ? 1 { 1 ? ∣ Φ ( t ) ∣ 2 } E\{|\Phi_n(t) - \Phi(t)|^2\} = n^{-1} \{1 - |\Phi(t)|^2\} E{∣Φn?(t)?Φ(t)∣2}=n?1{1?∣Φ(t)∣2}
由于 ∣ Φ ( 0 ) = 1 ∣ |\Phi(0)=1| ∣Φ(0)=1∣,对于任何连续型分布来说,对 t → ∞ t\to \infty t→∞来说, ∣ Φ ( t ) = 0 ∣ |\Phi(t)=0| ∣Φ(t)=0∣。因此,从上式看,经验特征函数在 0 点处精度最高,并沿着 t 趋近于无穷大的方向降低。换句话说, G ( t ) G(t) G(t) 应该在原点为中心的区间内具有较大的值。应当注意,精确区间与样本量有关 - 使得 T n T_n Tn? 可积。
于是这里取
d
G
(
t
)
=
g
(
t
)
dG(t) = g(t)
dG(t)=g(t):
g
(
t
)
=
α
S
2
π
exp
?
(
1
2
α
2
S
2
t
2
)
g(t) = \frac{\alpha S}{\sqrt{2 \pi}} \exp( \frac{1}{2} \alpha^2 S^2 t^2)
g(t)=2π?αS?exp(21?α2S2t2)
即一个均值为 0,方差为
1
α
S
2
\frac{1}{\alpha S}^{2}
αS1?2 的正态分布。其中
α
>
0
\alpha>0
α>0 为样本量系数,用以调整不同样本量对应的精确区间。并得到
T
n
T_n
Tn? 的如下:
T
(
α
)
=
n
?
2
∑
j
=
1
n
∑
k
=
1
n
exp
?
{
?
1
2
(
X
j
?
X
k
)
2
/
(
α
2
S
2
)
}
?
2
n
?
1
(
1
+
α
?
2
)
?
1
/
2
∑
j
=
1
n
exp
?
[
?
1
2
(
X
j
?
X
)
2
/
{
S
2
(
1
+
α
2
)
}
]
+
(
1
+
2
α
?
2
)
?
1
/
2
\begin{aligned} T(\alpha)=n^{-2} & \sum_{j=1}^{n} \sum_{k=1}^{n} \exp \left\{-\frac{1}{2}\left(X_{j}-X_{k}\right)^{2} /\left(\alpha^{2} S^{2}\right)\right\} \\ &-2 n^{-1}\left(1+\alpha^{-2}\right)^{-1/2} \sum_{j=1}^{n} \exp \left[-\frac{1}{2}\left(X_{j}-X\right)^{2} /\left\{S^{2}\left(1+\alpha^{2}\right)\right\}\right]+\left(1+2 \alpha^{-2}\right)^{-1/2} \end{aligned}
T(α)=n?2?j=1∑n?k=1∑n?exp{?21?(Xj??Xk?)2/(α2S2)}?2n?1(1+α?2)?1/2j=1∑n?exp[?21?(Xj??X)2/{S2(1+α2)}]+(1+2α?2)?1/2?
考虑到
α
\alpha
α 的择定没有理论依据,而根据参考文献 [4] 的工作,采用
α
=
1
\alpha=1
α=1 时,势函数会比较好。所以这里推荐采用
T
n
T_n
Tn? 公式如下:
T
n
=
2
n
?
1
∑
1
?
j
<
k
?
n
exp
?
[
?
1
2
(
X
j
?
X
k
)
2
/
S
2
]
?
2
1
/
2
∑
j
=
1
n
exp
?
[
?
1
4
(
X
j
?
X
ˉ
)
2
/
S
2
]
+
n
3
?
1
/
2
+
1
\begin{aligned} T_{n}=& 2 n^{-1} \sum_{1 \leqslant j<k \leqslant n} \exp \left[-\frac{1}{2}\left(X_{j}-X_{k}\right)^{2} / S^{2}\right]-2^{1 / 2} \sum_{j=1}^{n} \exp \left[-\frac{1}{4}\left(X_{j}-\bar{X}\right)^{2} / S^{2}\right] \\ &+n 3^{-1 / 2}+1 \end{aligned}
Tn?=?2n?11?j<k?n∑?exp[?21?(Xj??Xk?)2/S2]?21/2j=1∑n?exp[?41?(Xj??Xˉ)2/S2]+n3?1/2+1?
应用步骤
基于一系列对
T
n
T_n
Tn? 的伪随机数的蒙特卡罗方法,可以得出
T
n
T_n
Tn? 在各个分位点如下:
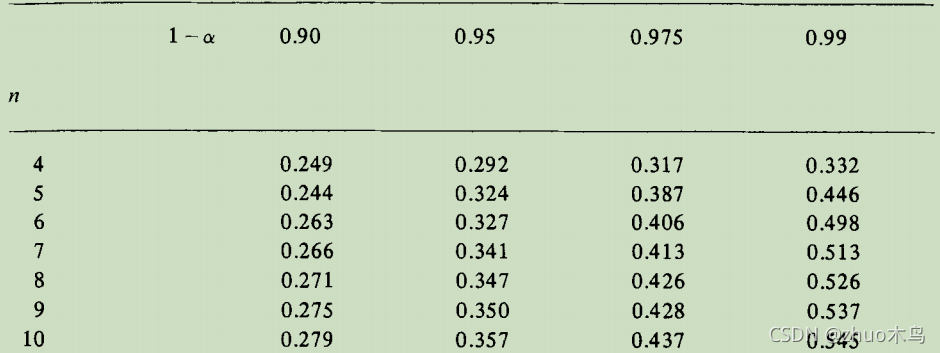
当
n
≥
10
n\geq 10
n≥10 时,需要对
T
n
T_n
Tn? 进行一定的修正
T
n
?
=
(
T
n
?
0.365
n
?
1
+
1.34
n
?
2
)
(
1
+
1.3
n
?
1
)
T_n^* = (T_n - 0.365n^{-1} + 1.34 n^{-2})(1+1.3 n^{-1})
Tn??=(Tn??0.365n?1+1.34n?2)(1+1.3n?1)
并进行一定的变换:
Z
n
=
γ
+
δ
?
log
?
(
(
T
n
?
?
ξ
)
/
(
ξ
+
λ
?
T
n
?
)
)
Z_{n}=\gamma+\delta \cdot \log \left(\left(T_{n}^{*}-\xi\right) /\left(\xi+\lambda-T_{n}^{*}\right)\right)
Zn?=γ+δ?log((Tn???ξ)/(ξ+λ?Tn??))
其中:
γ
=
3.55295
,
δ
=
1.23062
,
λ
=
2.26664
,
ξ
=
?
0.020682
\gamma=3.55295, \delta=1.23062, \lambda=2.26664, \xi=-0.020682
γ=3.55295,δ=1.23062,λ=2.26664,ξ=?0.020682;对数是以自然数
e
e
e 为底。
于是,要判断样本是否正态,可以:将 T n T_{n} Tn? 与 上表的临界值进行比较,若大于,则拒绝原假设,认为样本不是正态分布的。当 n ≥ 10 n\geq 10 n≥10时,将 Z n Z_n Zn?与标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1) 的分位数进行比较,若大于,拒绝原假设。
Python 实现
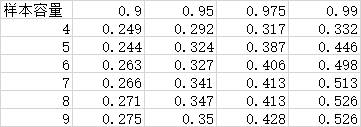
先在放代码的文件夹下面放一个 excel 表格,取名为 critical_table,然后输入如下数据:
# -*- coding: utf-8 -*-
"""
Created on Thu Sep 9 15:16:01 2021
@author: zhuo 木鸟
epps_pulley 检验;根据各类文献写成,可参考博客:
"""
import numpy as np
import pandas as pd
from scipy.stats import norm
def epps_pulley_test(x, alpha=0.05):
'''
对数据 x 进行 epps_pulley 正态检验,依据标准为 4882-1 的第 18 页。
Parameters
----------
x : pd.Series / np.array / list / pd.DataFrame
用于正态检验的数据.
Returns
-------
test_statistic : float
正态检验的检验统计量
'''
# 判断数据的数据类型是否符合要求,并将数据类型转换为 np.array
if isinstance(x, pd.Series):
x = np.array(x)
elif isinstance(x, pd.DataFrame):
#若数据类型为 pd.dataframe,那么将数据的第1列转换为 np.array
#其他列则不考虑
x = x.iloc[:,0].values
elif isinstance(x, list):
# 若数据为普通的Python数列
x = np.array(x)
elif isinstance(x, np.ndarray):
pass
else:
raise(Exception('输入数据类型不符合要求,输入数据必须为序列, dataframe, numpy 数列和 Python 列表'))
# 判断数据的维度是否为一维,否则抛出错误
if len(x.shape) != 1:
raise(Exception('输入数据必须是一维的'))
# 求解数据的均值
x_bar = np.mean(x)
# 求解数据的方差(二阶中心矩)
m2 = np.var(x)
# 样本量
n = len(x)
# 中间数据 A,为统计量 Tn 的第三项(这里Tn 是标准 4882 中的 TEP)
# 中间数据 A、B 的定义可见 4882 的式 15 和 图 8
A = 0
# 根据公式15求A
for i in range(1,n):
# 从 0 到 n-1 进行求和(所有数据)
for k in range(i):
# 从 k 到 i 进行求和
diff = -(x[i]-x[k])**2
A = A + np.exp(diff/(2*m2))
# 求出 A
A = 2/n*A
# 求出 B,为统计量 TEP 的第四项
B = -np.sqrt(2)*np.sum(np.exp(-(x-x.mean())**2/(4*m2)))
# 求出统计量
Tn = 1 + n/np.sqrt(3) + A + B
# 判断数据是否属于正态分布
if n < 4:
raise(Exception('Epps-Pulley 检验使用时,数据量要在 4 个及以上才能获得精确结果'))
elif n < 10:
# 若 样本量 小于 10 个,则可以直接从模特卡罗法
# 得出的临界值表格中找出临界值,并判断
if 1-alpha in (0.9, 0.95, 0.975, 0.99):
#戒指表来自于博客的参考文献的第4节
critical_table = pd.read_excel(r'./epps_pulley_test_critical_value.xlsx')
critical_value = critical_table.loc[critical_table['样本容量']==n][1-alpha]
critical_value = float(critical_value)
test_statistic = Tn
else:
raise(Exception('请选择常用的显著水平'))
else:
# 博客参考文献三的第4小节中的动态检验步骤的代码实现
Tn_star = (Tn - 0.365/n + 1.34/(n**2))*(1 + 1.3/n)
gamma = 3.55295
delta = 1.23062
lam = 2.26664
xi = -0.020682
# 以自然数 e 为底
Zn = gamma + delta*np.log((Tn_star-xi)/(xi+lam-Tn_star))
critical_value = round(norm.ppf(1-alpha), 2)
test_statistic = round(Zn, 2)
if n < 10:
print('使用 Tn 进行判断,输出的检验统计量为 Tn')
else:
print('使用 Zn 进行判断,输出的检验统计量为 Zn')
if test_statistic > critical_value:
print(f'经检验,在显著性水平为{1-alpha}的前提下,样本不服从正态分布')
return False, critical_value
else:
print(f'经检验,在显著性水平为{1-alpha}的前提下,样本服从正态分布')
return True, critical_value
if __name__ == '__main__':
# 标准 4882 的第十六页的表格 5 的数据(变换前)
# 已经过验证
x_before = np.array([147, 186, 141, 183, 190, 123, 155, 164, 183, 150, 134,
170, 144, 99, 156, 176, 160, 174, 153, 162, 167,
179, 78, 173, 168])
epps_pulley_test(x_before)
# 标准 4882 的第 16 页的表格5的变换后的数据,数据是满足正态检验的
x_after = np.array([1.756, 1.255, 1.799, 1.322,
1.146, 1.908, 1.690, 1.602,
1.322, 1.732, 1.845, 1.531, 1.778,
2.021, 1.681, 1.447, 1.643, 1.477,
1.708, 1.623, 1.568, 1.398, 2.100,
1.491, 1.556])
epps_pulley_test(x_after)
Monte-Carlo 法产生临界值
在本博客的参考文献三里面,有大致介绍了采用 epps-pulley 时,检验统计量的临界值数据表。本博客的前文中也给出了这个表。那么这个表是如何产生的呢?根据参考文献里的说法,是采用了蒙特卡罗的方法产生的,具体如何做呢?下面本文将结合Python程序,用蒙特卡罗法来实现临界值表的产生。
首先我们知道检验统计量 Tn 的判断临界值,应是在原假设也即样本服从正态分布的前提下产生的。检验统计量亦是一个随机变量,但其具体的分布形式我们很难求出,于是只能采用产生随机数的方式去拟合出一个累计分布函数。具体原理如下:
由于原假设为样本服从正态分布,因此我们可以考虑产生200000个,从标准正态分布总体中抽取的随机数,并计算在样本容量 n 为某个特定值的情况下的检验统计量的取值。
样本容量 n = 4 n=4 n=4 为例,我们于是便产生了200000个 Tn,并将这200000个 Tn 数据按升序方式排序,并找到排在 ? 200000 × p ? \lceil 200000 \times p \rceil ?200000×p? 的数的取值,于是便可以找出 p- 分位数。
import numpy as np
def critical_value_monte_carlo(n=4, percentile=0.99):
'''
大家可以设置参数,并对照博客的参考文献 3 里面的表格来看看,用该程序产生的临界值是否一致
Parameters
----------
n : int
样本容量.
percentile : float
分位数. The default is 0.99.
Returns
-------
None.
'''
# n 为样本容量,这里的样本容量是针对 Tn 来说的
# 产生 200,000 个伪随机数
pseudo_random = np.random.uniform(0, 1, size=(200000,n))
# 求解 Tn
# 求解数据的均值
x_bar = np.mean(pseudo_random, axis=1)
# 求解数据的方差(二阶中心矩)
m2 = np.var(pseudo_random, axis=1)
# 中间数据 A,为统计量 Tn 的第三项(这里Tn 是标准 4882 中的 TEP)
# 中间数据 A、B 的定义可见 4882 的式 15 和 图 8
Tn_list = []
A = 0
# 根据公式15求A
for i in range(1,n):
# 从 0 到 n-1 进行求和(所有数据)
for k in range(i):
# 从 k 到 i 进行求和
diff = -(pseudo_random[:,i]-pseudo_random[:,k])**2
A = A + np.exp(diff/(2*m2))
# 求出 A
A = 2/n*A
# 求出 B,为统计量 Tn(TEP) 的第四项
diff = (pseudo_random.T-x_bar).T
diff = -diff**2
div = (diff.T/(4*m2)).T
B = -np.sqrt(2)*np.sum(np.exp(div), axis=1)
# 求出统计量
Tn = 1 + n/np.sqrt(3) + A + B
Tn.sort()
print(f'样本容量为 {n} 的检验统计量 Tn 的 {percentile}- 分位数为:{Tn[round(200000*percentile)]}')
critical_value_monte_carlo(4, 0.99)
大家只要修改函数的参数:n 和 percentile,就可以得到想要检验统计量 Tn 的 p-分位数 啦。