前言
一次巧合的情况下点开了一个ctf比赛 一直没玩过ctf 第一次 0基础分析 签到题
crypto的
题目:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Crypto.Util.number import *
import random
flag=b'flag{******************}'
n = 2 ** 256
flaglong=bytes_to_long(flag)
m = random.randint(2, n-1) | 1
c = pow(m, flaglong, n)
print('m = ' + str(m))
print('c = ' + str(c))
# m = 73964803637492582853353338913523546944627084372081477892312545091623069227301
# c = 21572244511100216966799370397791432119463715616349800194229377843045443048821
开始啥都不会
先通过找师傅帮忙 给出了 解密的脚本
m = 73964803637492582853353338913523546944627084372081477892312545091623069227301
c = 21572244511100216966799370397791432119463715616349800194229377843045443048821
n = 2 ** 256
import sympy
flag=sympy.discrete_log(n,c,m)
print(flag)
import binascii
print(hex(flag))
print(hex(flag)[2:])
print(binascii.unhexlify(hex(flag)[2:]))#将答案的十六进制转出来就行
print(binascii.hexlify(b'flag{DASCTF_zjut}'))
运行结果

先分析题目
主要的地方在
c = pow(m, flaglong, n) 这一段代码
这段代码可以看出只有flaglong是我们不知道的
所以就需要反解出flaglong
c = pow(x,y,z):这个是表示x的y次幂后除以z的余数。
所以要求y 就相当于求flaglong
根据师傅的帮助 这道题就可以转化为
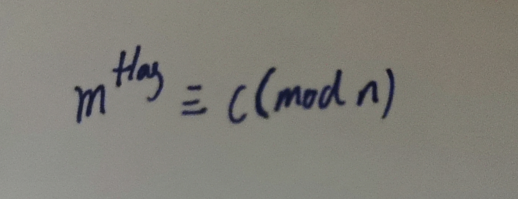
求满足m的flag次方等于c对模n取同余
“≡”是数论中表示同余的符号
discrete_log这个函数就是用来求这种类型的
discrete_log(x,y,z),x是模数,y是余数,z是底数
sympy.discrete_log(n,c,m) 就相对于上面的c = pow(m, flaglong, n)
c是余数 m是底数 n是模数
**flag=sympy.discrete_log(n,c,m)**这样解出来的flag就是flaglong 是十进制数 因为开始是通过bytes_to_long函数转化的 所以要转化为字符
十进制转化为字符 要先转化为16进制 然后转化为字符
所以用hex先转化为16进制 然后截取掉 进制标志位
然后在通过binascii.unhexlify()函数转化为字符
也可通过在线的进制转化
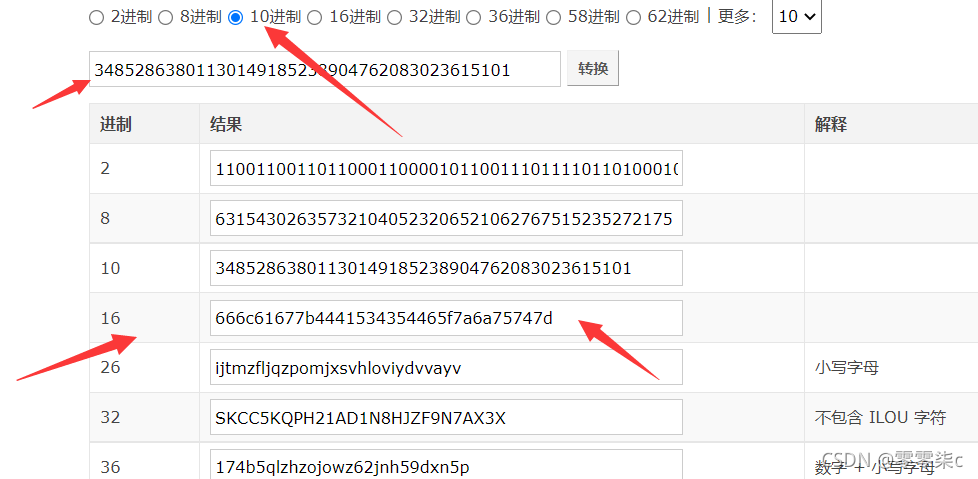

最后也可以通过Crypto 库的另一个函数直接转化flag字符
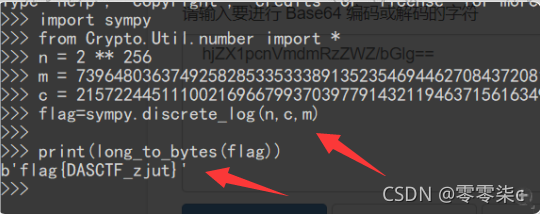
但是这里我本地不知道什么原因用不起Crypto 就没有在本地复现了
成功解出flag