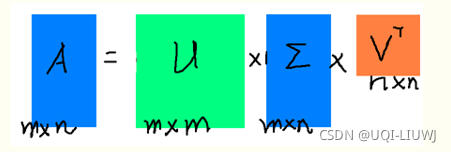1 ndarray
1.1 创建
np.array(object,dtype=…) | 用object创建ndarray
? |
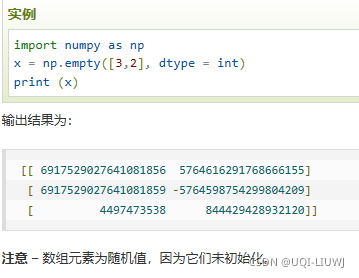
empty(shape,dtype=) | 指定形状&类型,元素值均为随机值
|
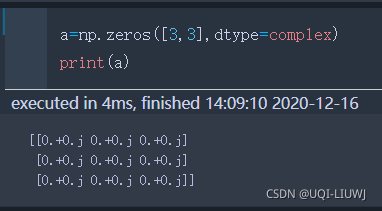
zeros(shape,dtype=) | 填充0
|
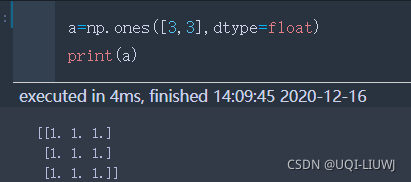
ones | 填充1
|
full(shape,num,dtype) | 用num填充shape大小的数组
|
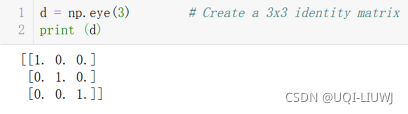
eye(num,dtype)等同于identity(num,dtype) | num*num的单位矩阵
|
random.random(shape,dtype) |  |
diag | 当?np.diag(array)?中 array是一个1维数组时,结果形成一个以一维数组为对角线元素的矩阵 array是一个二维矩阵时,结果输出矩阵的对角线元素
|
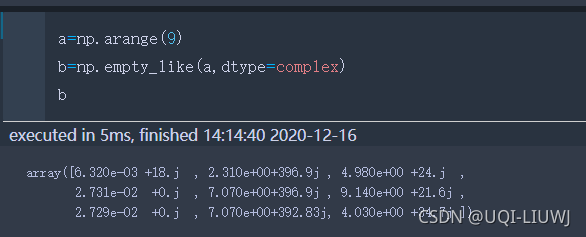
empty_like(x) | 创建一个形状和x一样的,数值随机
|
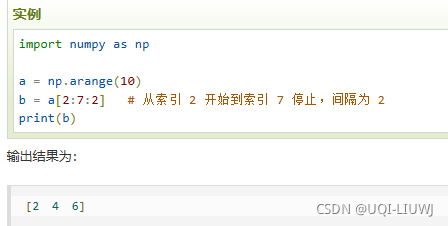
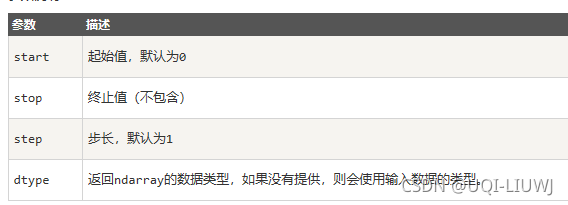
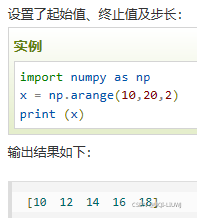
arange(start, stop, step, dtype) |
|
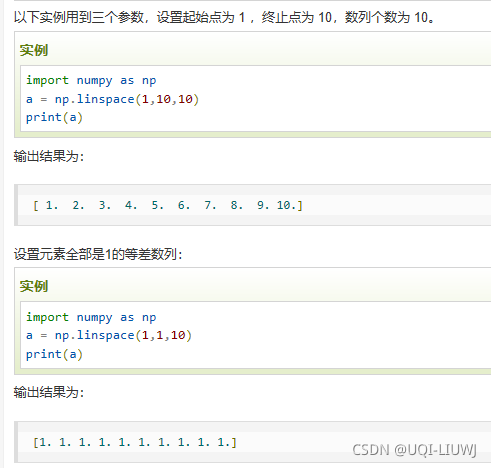
linspace | 创建一个等差数列
? |
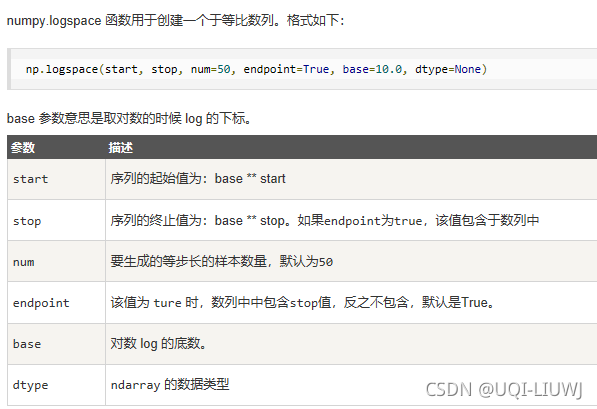
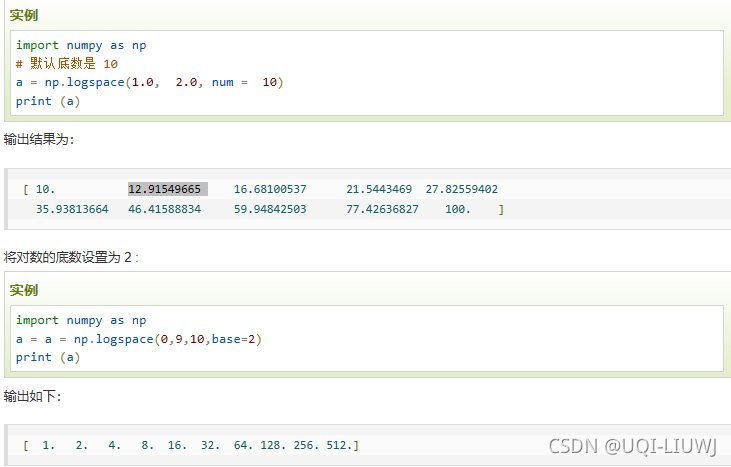
logspace | 创建一个等比数列
? |
?1.2?ndarray 属性
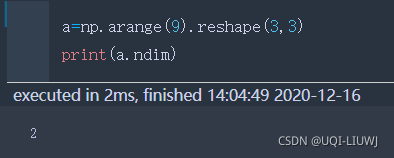
ndim | 矩阵维数 |
|
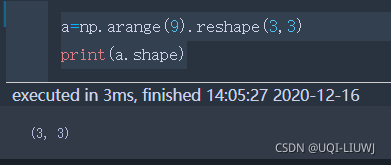
shape | 数组的维度(元组形式)【用reshape调整大小】 |
|
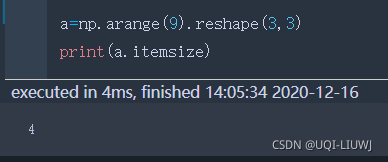
itemsize | 一个元素的大小(占几个字节) |
|
real | 元素的实部 |
|
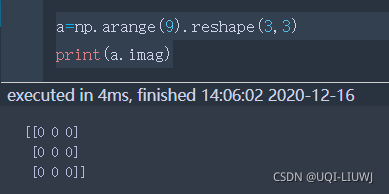
imag | 元素的虚部 |
|
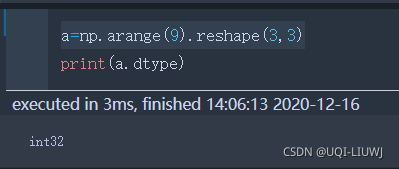
dtype | 数据类型 |
|
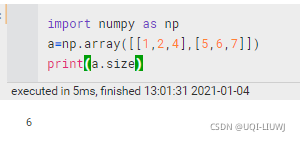
size | 元素个数 |
|
1.3 切片
| a[start:end:step] | 左闭右开
|
| a[…,x]——第x+1列 a[x,…]——第x+1行 | 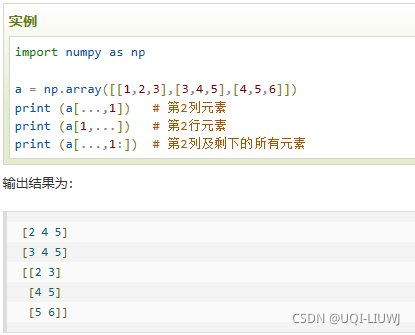 |
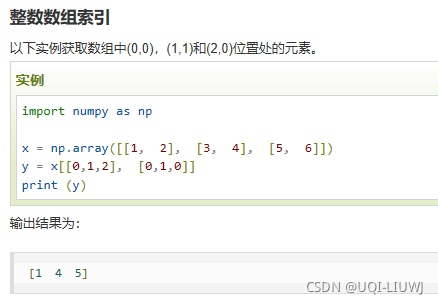
| a[[list1],[list2]] | 获取 (list1[0].list2[0]) (list1[1].list2[1]) (list1[2].list2[2]) ….等索引位置的数据
? |
| a[list] | 获取list中这几行元素
|
| a[np.ix_([list1],[list2])] |
获取第list1行的第list2列的数据
? |
1.3.1 切片的性质?
切片是原来的array的一个视图,修改切片的话,原来的也改变了

!!!记住结论:!!!
如果是数字/带数字的':'来切片的话,不论是不是有塌缩(类似于r1那样的变成一维的)都是原来的的一个view,元素修改了就一起修改了
如果是数组这样的索引切片的话(注:元组tuple不行),那么就是copy不是view了
如果是混合的(一个数组,一个纯数字),那么就是copy(因为有数组切片了)
import numpy as np
a=np.array([[1,2,3],[3,4,5],[7,8,9]])
b=a[1,:]
c=a[[1],:]
d=a[1:2,:]
print(a,'\n',b,c,d)
'''
[[1 2 3]
[3 4 5]
[7 8 9]]
[3 4 5] [[3 4 5]] [[3 4 5]]
'''
b[1]=10
print(a,'\n',b,c,d)
'''
[[ 1 2 3]
[ 3 10 5]
[ 7 8 9]]
[ 3 10 5] [[3 4 5]] [[ 3 10 5]]
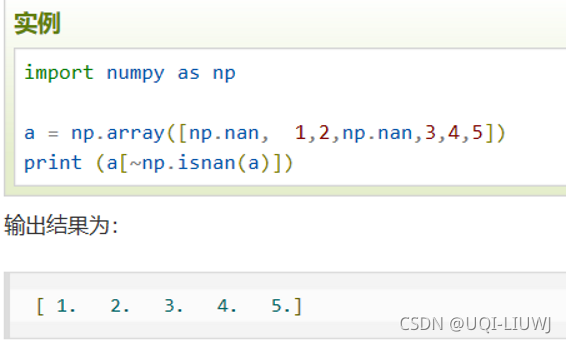
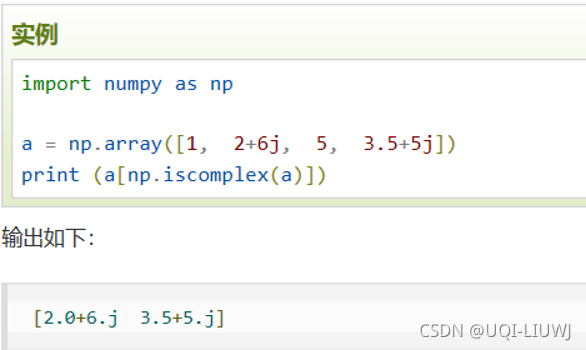
'''?1.4 布尔索引
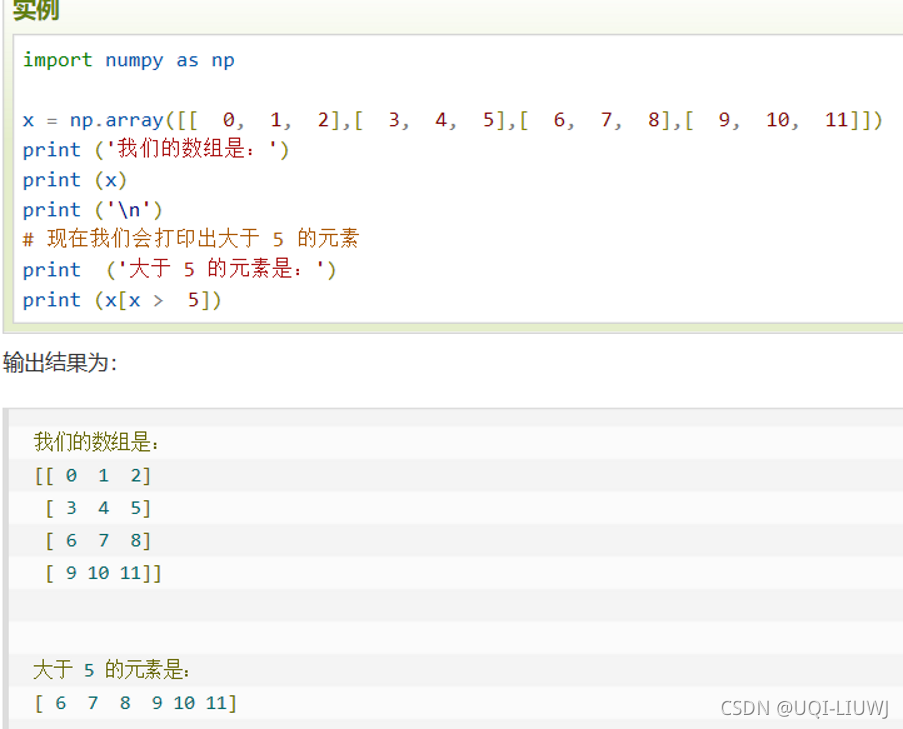
?
?
?2? 数组运算
?执行数组的运算必须有相同的行列/符合广播规则
2.1 相同行列
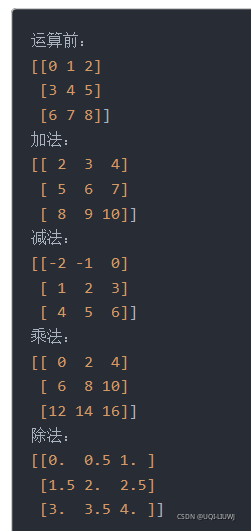
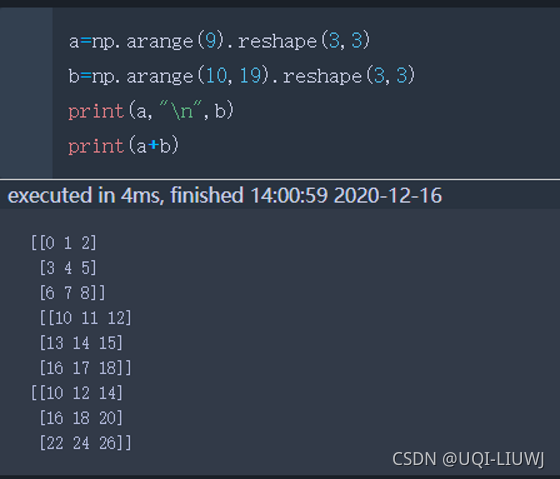
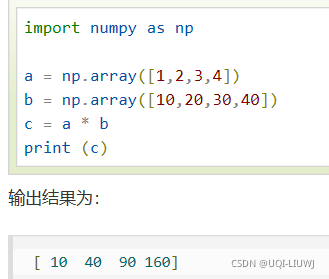
相同行列:对应元素加减乘除
?
?
2.2 广播原则?
?当运算中的 2 个数组的形状不同时,numpy 将自动触发广播机制
2.2.1 数组+标量
?
?
?2.2.2 数组+行/列
?

3 内积外积与矩阵乘法?
?3.1 外积

?
?3.2 内积
内积——inner/dot
?np.dot(a,b)等价于a.dot(b)
3.3 乘法
matmul/@/dot
?4 函数
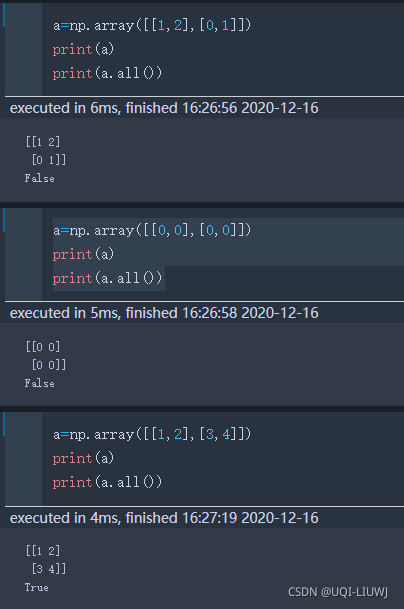
all | 矩阵中元素是否全部非零
| ||||||||||||||||||
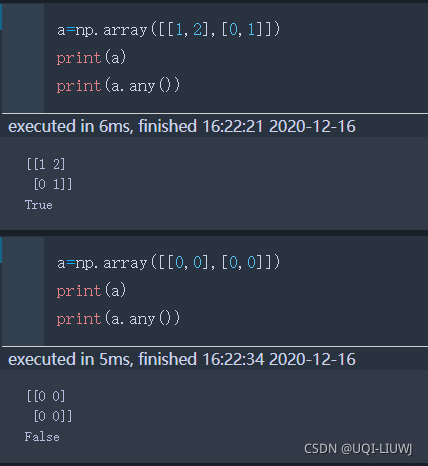
any | 矩阵中是否有元素非零
| ||||||||||||||||||
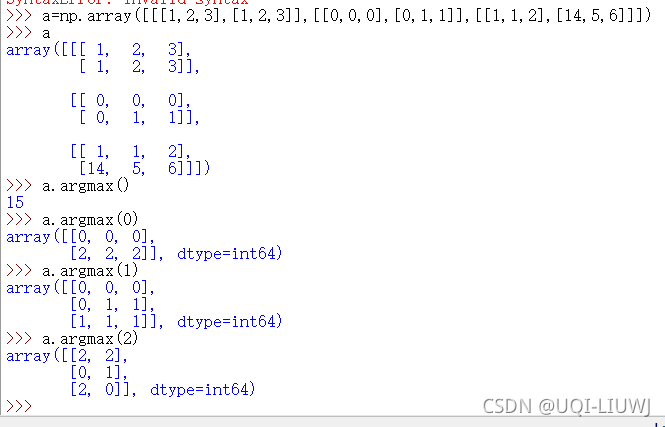
argmax/argmin | 第几维度的最大最小值的坐标
Argmax[0]:对每一个a[…][0][0],a[…][0][1],a[…][0][2] a[…][1][0],a[…][1][1],a[…][1][2]找一个最大值 | ||||||||||||||||||
argsort | argsort函数返回的是数组值从小到大的索引值
?
b——正序 -b——倒序 如果是多维的话(默认是最大的一个axis) Axis=0 a[..][0][0],a[…][0][1],a[…][0][2] a[..][1][0],a[…][1][1],a[…][1][2]
Axis=1 a[0][…][0],a[0][…][1],a[0][…][2]
Axis=2同理
| ||||||||||||||||||
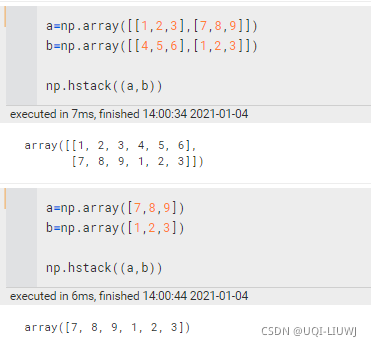
np.c_ | 按行连接两个矩阵,就是把两矩阵左右相加,要求行数相等
注意和hstack的区别,hstack里面是把一行的向量作为一行来看的,r_里面是当作一列来看待的
| ||||||||||||||||||
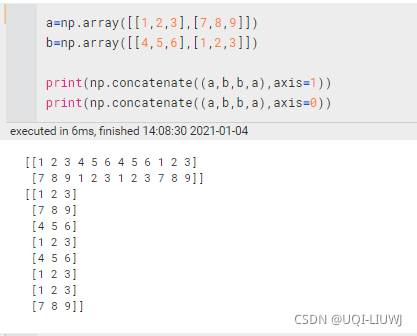
| concatenate | 和vstack,hstack差不多,不过用axis来指定是行还是列
axis=1 行——a[0][......] axis=0 列——a[......][0] | ||||||||||||||||||
copy |
这个是真copy,不是view | ||||||||||||||||||
clip | 截取数组中在min和max之间的部分,比min小的置为min,比max大的置为max
| ||||||||||||||||||
cumsum/cumprod | 括号是几——第几维度累加/累乘(a[][][][]里面的第几个,从左往右) 括号里是0:原第一行=原第一行 ? 原第二行=原第二行+原第一行 ? 原第三行=原第三行+原第二行+原第一行 括号里是1:列的操作 没有字母,所有元素,一个一个叠加
| ||||||||||||||||||
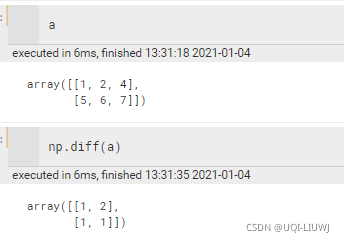
diff | 类差运算
| ||||||||||||||||||
flatten | 返回一份数据拷贝,对拷贝所做的修改不影响原始数组
F风格:按列展开 flat 一个迭代器
| ||||||||||||||||||
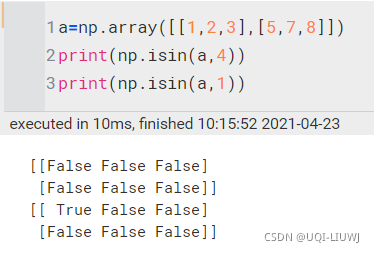
np.isin(a,b) | ?用于判定a中的元素在b中是否出现过,如果出现过返回True,否则返回False,最终结果为一个形状和a一模一样的数组。
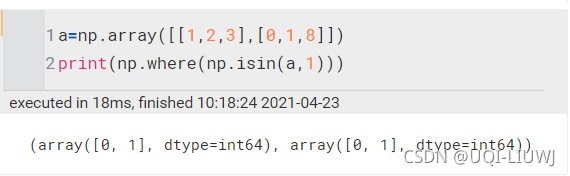
和np.where搭配使用,效果更好(np.where返回True的坐标)
分别是我找到的1的第一维坐标和第二位坐标 | ||||||||||||||||||
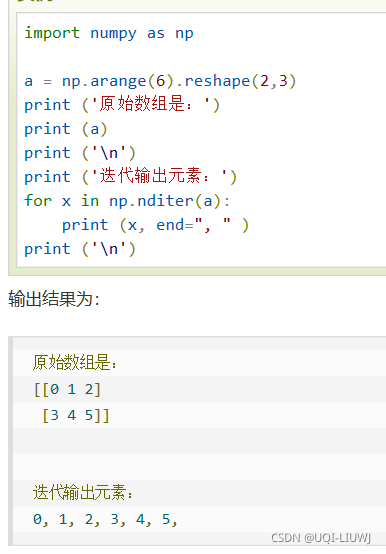
nditer | 按照ndarray在内存中的存储顺序逐个访问
a和a转置在内存中的存储顺序一样——他们的遍历顺序一样
默认order=’C‘行优先 ——order=“F’(fortran 列优先)? | ||||||||||||||||||
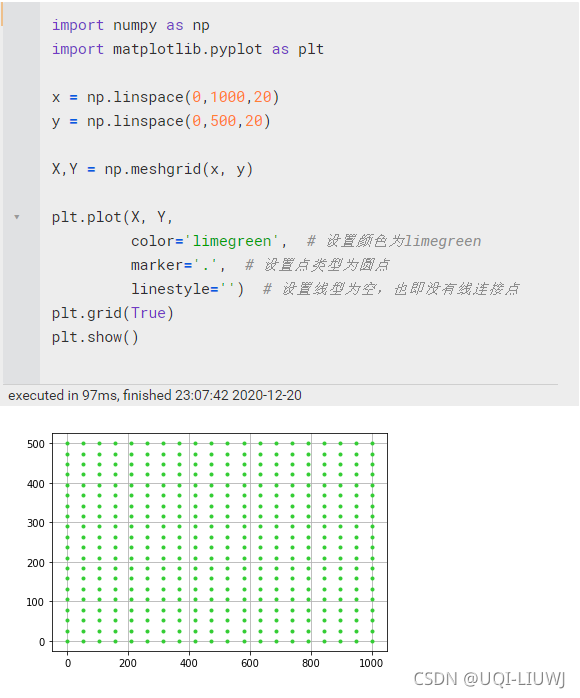
meshgrid(ndarray,ndarray) | 返回坐标方格的X与Y x和y都是二维数组,分别是这些点的横坐标/纵坐标
| ||||||||||||||||||
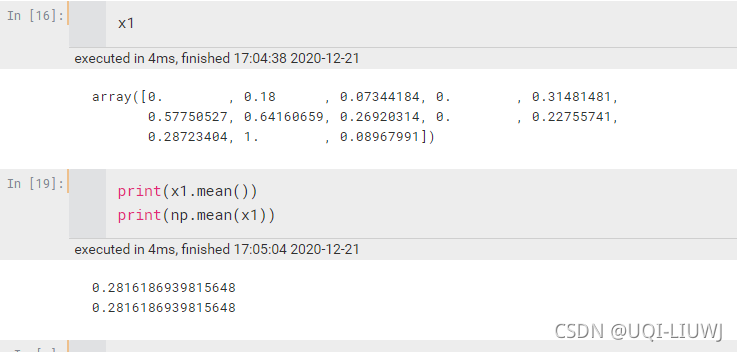
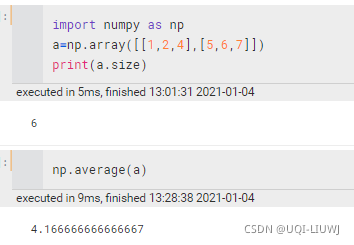
mean/average | 计算平均数,加axis就是某一个轴, 比如axis=0,就是每一列一个平均数(a[;;;][0],a[,,,,][1],…..,)
average只能是np.average
| ||||||||||||||||||
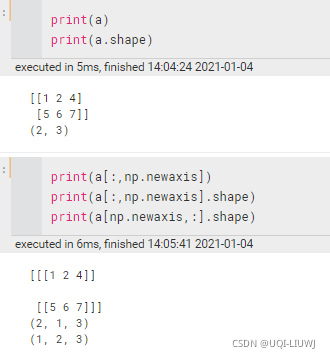
newaxis | 添加一个维度
感觉还是reshape靠谱一点 | ||||||||||||||||||
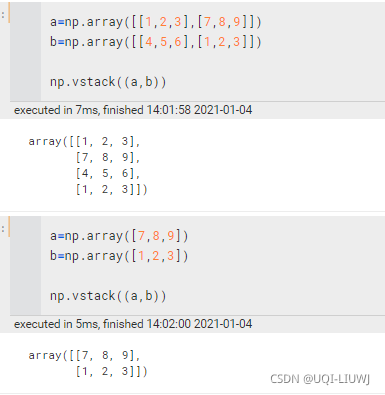
np.r_ | 按列连接两个矩阵,就是把两矩阵上下相加,要求列数相等
注意和vstack的区别,vstack里面是把一行的向量作为一行来看的,r_里面是当作n行来看待的
| ||||||||||||||||||
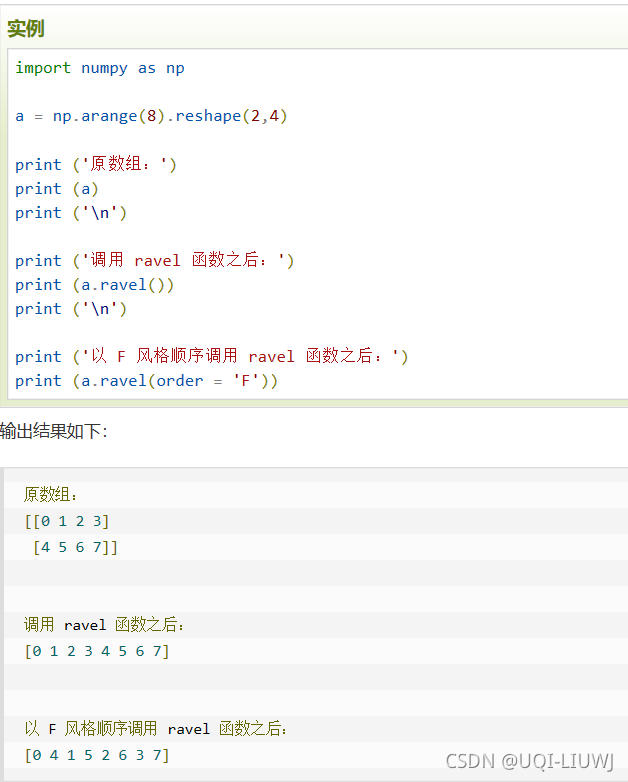
ravel | 和flatten差不多,唯一的区别是,修改会影响原始数组
| ||||||||||||||||||
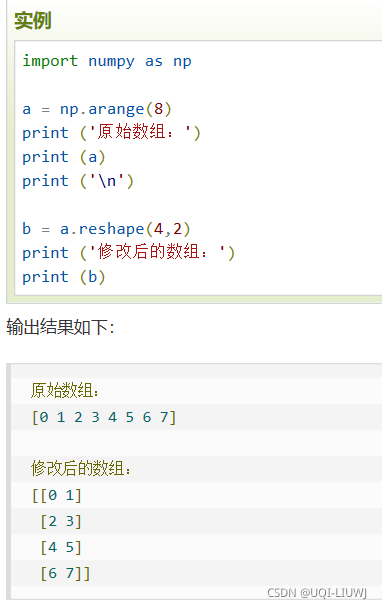
reshape |
| ||||||||||||||||||
resize | 如果一样大的话和a.reshape()差不多 shape比a的尺寸小的话,那就是截取
如果尺寸大的话,会把a的元素按照a的顺序补进去
| ||||||||||||||||||
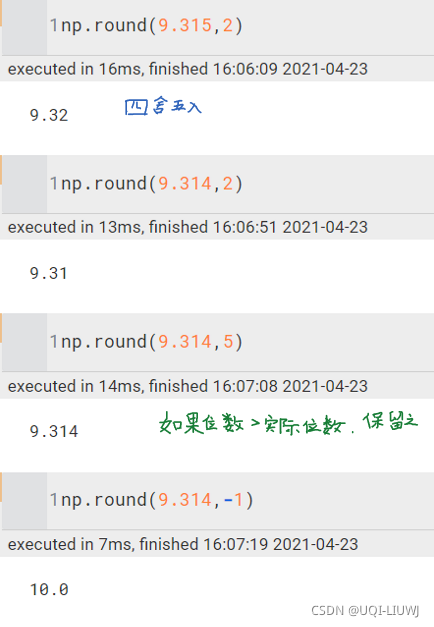
np.round | round( number ) 函数会返回浮点数 number 的四舍五入值 具体定义为 round(number[,digits]): 如果 digits>0 ,四舍五入到指定的小数位; 如果 digits=0 ,四舍五入到最接近的整数; 如果 digits<0 ,则在小数点左侧进行四舍五入; 如果 round() 函数只有 number 这个参数,则等同于 digits=0。
| ||||||||||||||||||
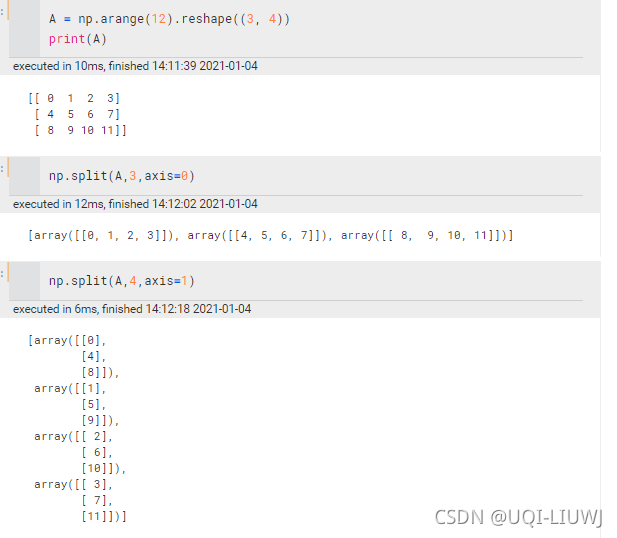
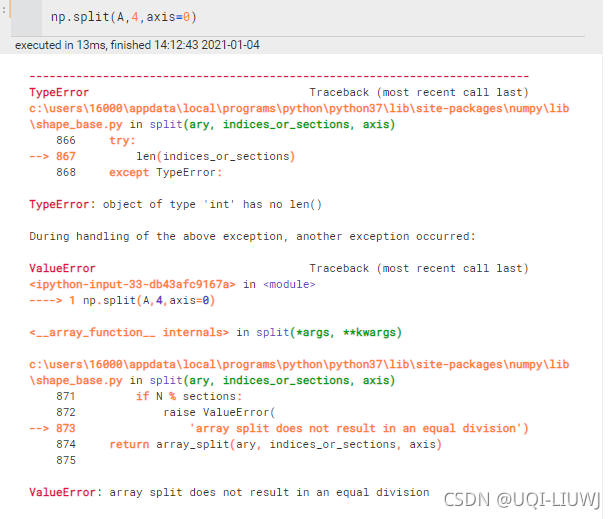
split | 等量对分 (axis=0 a[1~n][0]会被等分到各个里面去) 一定是等量,不等量的话会报错
vsplit=split(axis=0) hsplit=split(axis=1) | ||||||||||||||||||
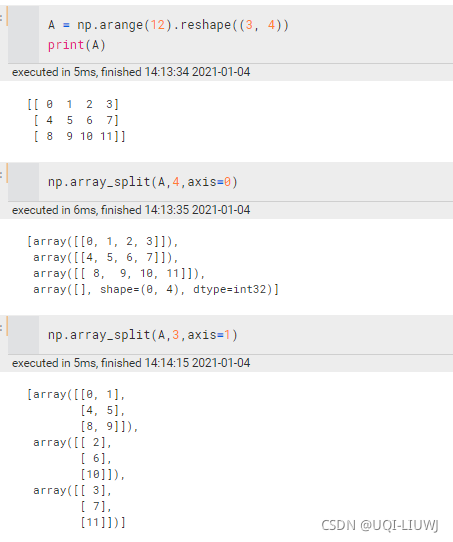
array_split | 不等量分割
| ||||||||||||||||||
np.sin | 逐元素取sin | ||||||||||||||||||
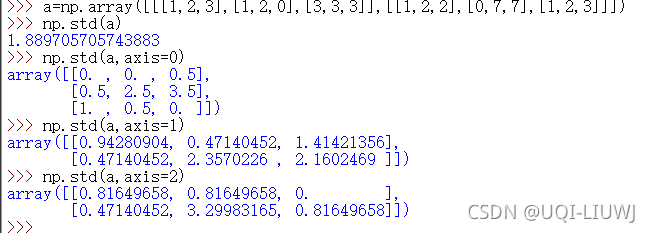
std | 计算标准差 Axis=0——计算a[…][0][0],a[…][0][1],…的标准差
| ||||||||||||||||||
squeeze | 删除单维度条目
| ||||||||||||||||||
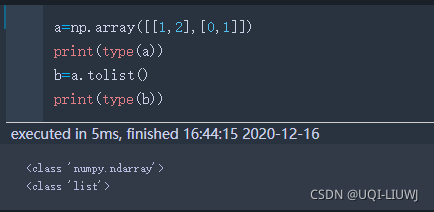
tolist | 转换为list
| ||||||||||||||||||
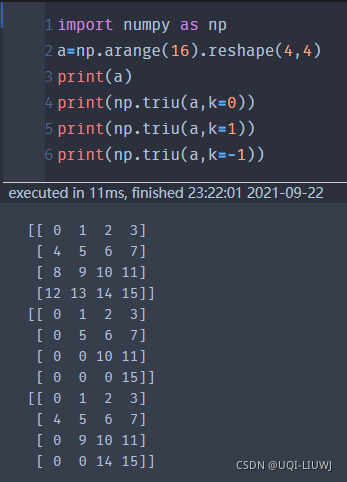
triu(data,k) | 以data为数据,创建一个上三角矩阵,k表示这个上三角的边接往上/下移动几条线的距离
| ||||||||||||||||||
tile | np.tile(a,(2))函数的作用就是将函数将函数沿着X轴扩大两倍。如果扩大倍数只有一个,默认为X轴
np.tile(a,(2,1))第一个参数为Y轴扩大倍数,第二个为X轴扩大倍数。本例中X轴扩大一倍便为不复制。
| ||||||||||||||||||
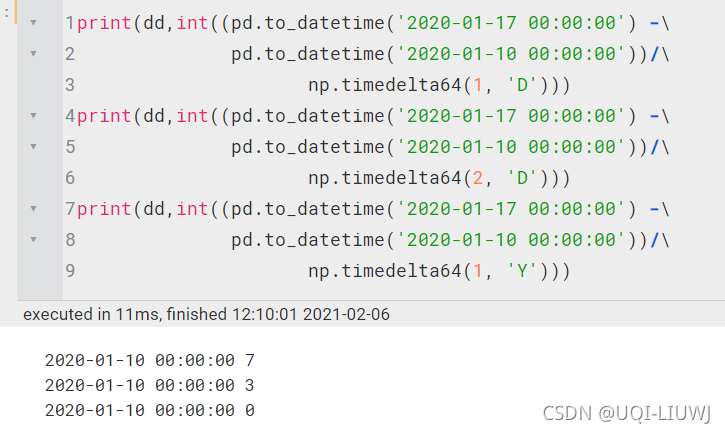
np.timedelta(num,'x') |
计算两个datetime中间差多少时间间隔(向下取整)【Y、M、W、D、h、m、s、ms、us、ns】 | ||||||||||||||||||
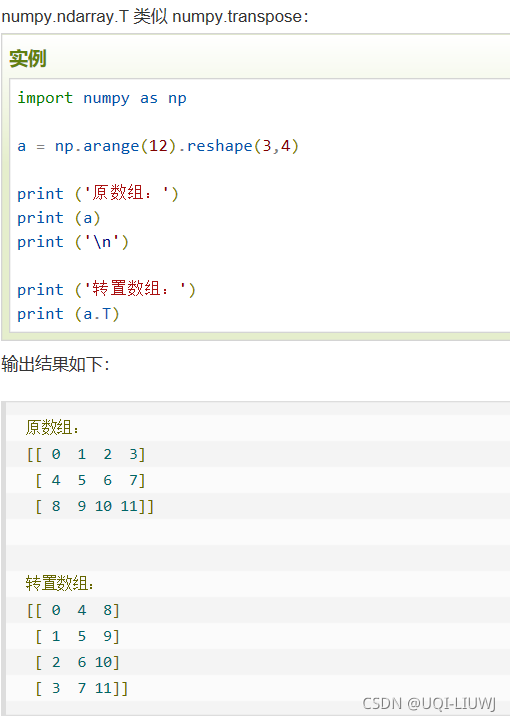
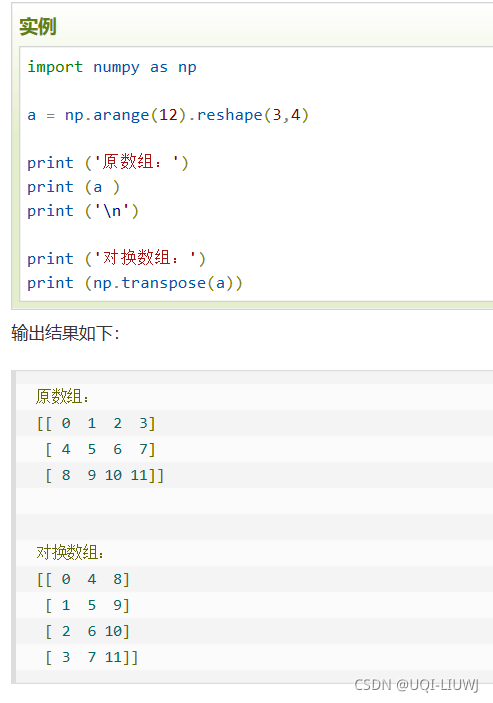
转置 |
| ||||||||||||||||||
where | numpy.where()?有两种用法: 1. np.where(condition, x, y) 满足条件(condition),输出x,不满足输出y。 2. np.where(condition) 只有条件 (condition),没有x和y,则输出满足条件 (即非0) 元素的坐标。 这里的坐标以tuple的形式给出,通常原数组有多少维,输出的tuple中就包含几个数组,分别对应符合条件元素的各维坐标。
|
5 文件处理
tofile() & fromfile() | tofile()将数组中的数据以二进制格式写进文件 tofile()输出的数据不保存数组形状和元素类型等信息 fromfile()函数读回数据时需要用户指定元素类型,并对数组的形状进行适当的修改
读入数据的时候,需要设置正确的dtype参数,并且修改属组的shape属性,才会得到和原始数据一致的结果 sep参数:tofile 和 fromfile中数值的分隔符 |
save() & load() | NumPy专用的二进制格式保存数据,它们会自动处理元素类型和形状等信息
|
savez() | 将多个数组保存到一个文件中 savez()的第一个参数是文件名,其后的参数都是需要保存的数组
?没有起名的话就是'arr_0","arr_1",....起来名字的就是所起的名字 |
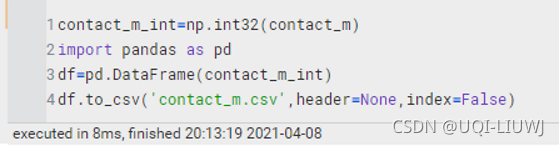
ndarray写入csv | 先转化成DataFrame
|
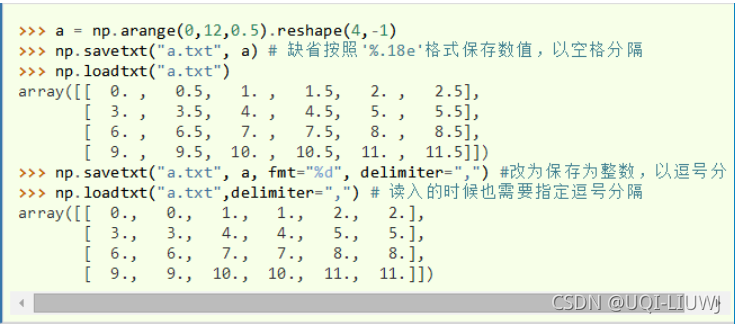
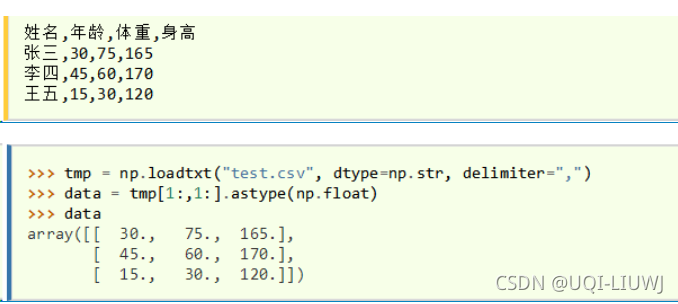
savetxt() & loadtxt() |
|
6 linalg
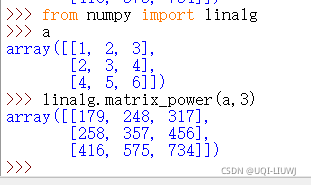
matrix_power | 矩阵的n次方
|
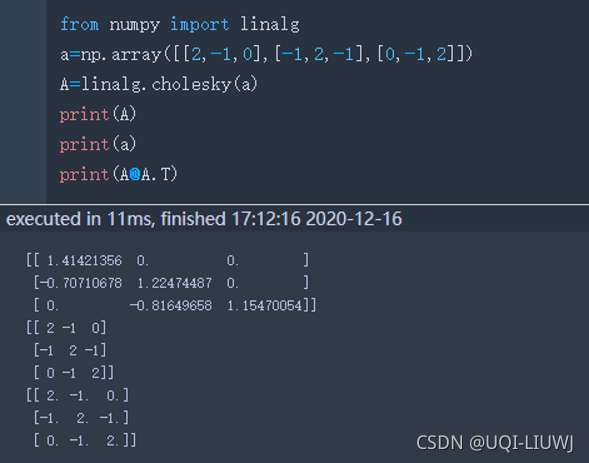
cholesky | 对称正定矩阵A——存在一个对角元为正数的下三角矩阵L,A=LL^T x=linalg.cholesky(A),出来的结果是A的L
|
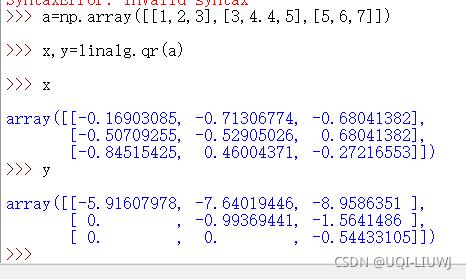
qr | QR分解 任何一个满秩矩阵,都可以用qr分解 一个正交矩阵和一个上三角矩阵
|
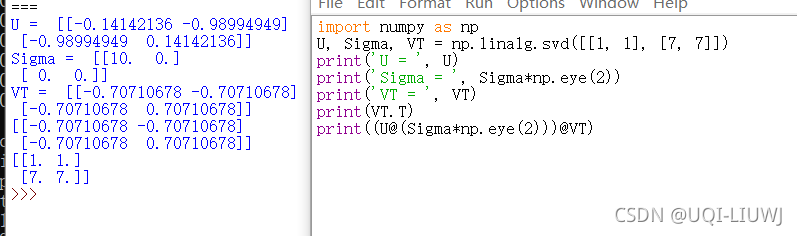
svd | SVD分解(一般用于降维
U,V——m,n阶方阵 Σ——除了对角线元素,都是0,对角线元素——奇异值
numpy出来的奇异值是从大到小排列的,所以直接切片就可以了 |
eig | 求特征值和特征向量
每一列就是一个特征向量 |
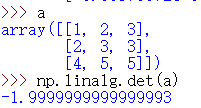
det | 求行列式
|
matrix_rank | 计算矩阵的秩
|
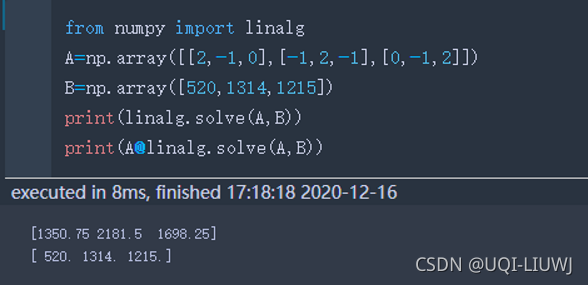
solve | Solve(a,b)_解ax=b的x
|
inv,pinv | 计算矩阵的逆/伪逆
|




 ??
??
 ?
?